
重心からみた2つの物体の弾性衝突の問題って,かなり複雑でわけがわからなくなるんだけど.結局何がいいたいんだろう??

重心からみた弾性衝突は次の2つのポイントを最終的に聞かれることが多いです.
- 重心からみると,衝突前の2つの物体運動は一直線上にあり,衝突後も(衝突前の直線とは限らないが)一直線上を運動する.
- 重心からみた物体の速度の大きさは衝突の直前後で変化しない.
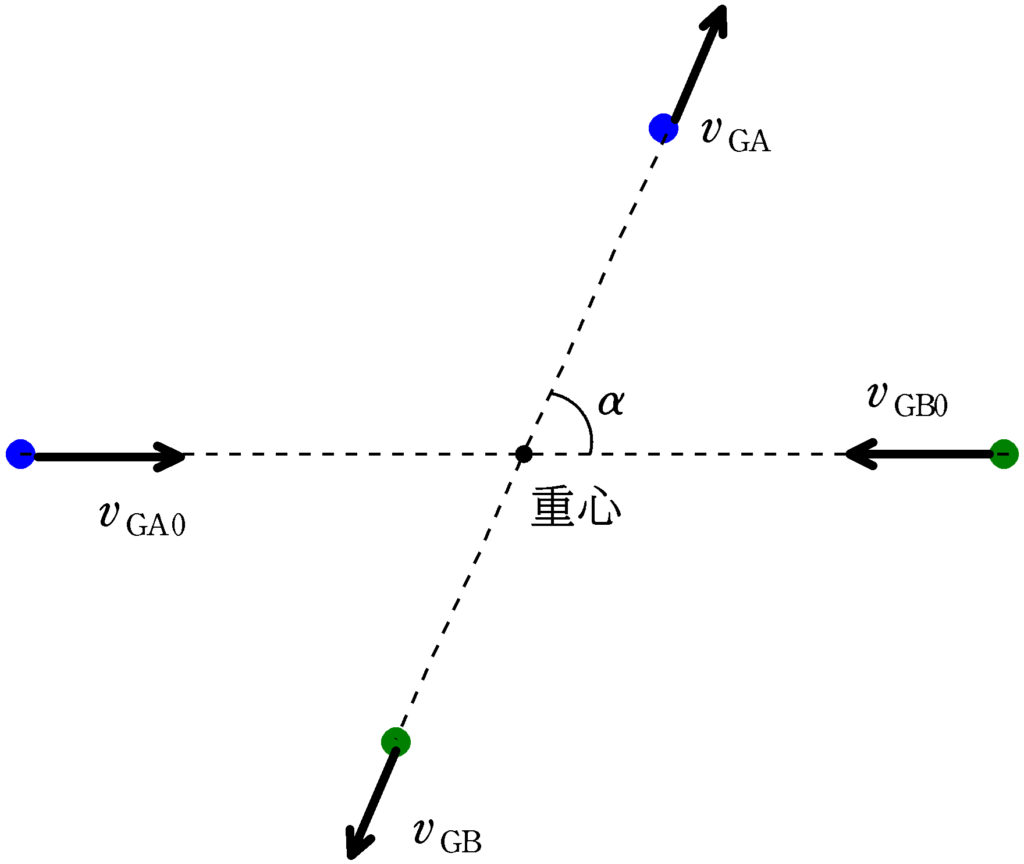

上図で$v_{\rm GA0}$,$v_{\rm GB0}$をそれぞれの重心からみた衝突前の速さ,$v_{\rm GA}$,$v_{\rm GB}$を重心からみた衝突後の速さとすると,
$v_{\rm GA0}=v_{\rm GA}$,$v_{\rm GB0}=v_{\rm GB}$
ってことか.一直線上にあるし,かなりきれいな運動をするんだね!

はい.今回,これを示すのに次のことを用います.
- 重心速度
- 衝突前の重心からみた速度
- 相対速度のベクトル図
- 重心からみた運動量の和は$0$
- 余弦定理
- 力学的エネルギー保存則
衝突前後の重心の速度
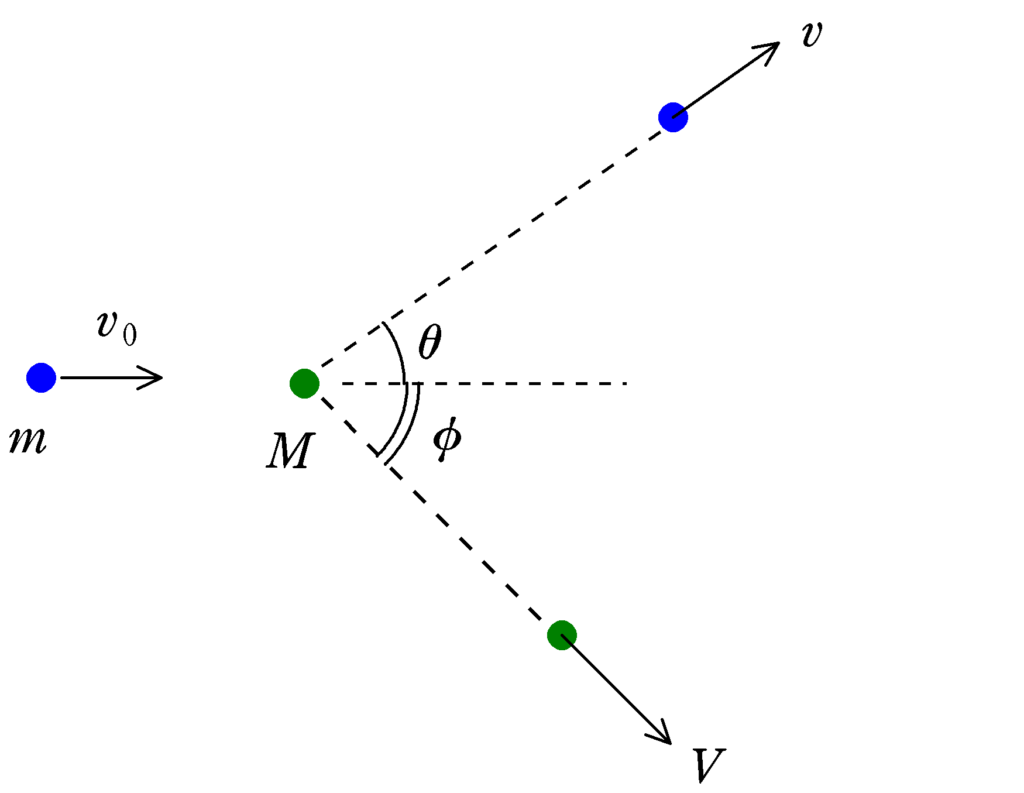

静止した質量$M$の物体(物体B)に速さ$v_{0}$の質量$m$の物体(物体A)が衝突し,衝突後の物体A,Bの速さが$v,V$とします.また,衝突後の速度の向きは衝突前のAの速度の方向よりそれぞれ$\theta,\phi$の方向であるとしましょう.
このとき,衝突前の重心速度$v_{\rm G}$は次のようになります.
速度$v_{1}$,$v_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心速度$v_{\rm G}$は
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
★ 衝突前の重心速度の式
$v_{\rm G}=\dfrac{M\times 0+mv_{0}}{M+m}=\dfrac{m}{M+m}v_{0}$
速度の向きは図の右方向

また,今回は衝突の際に互いに及ぼす力や万有引力や静電気力などの相互作用の力しかはたらかない場合を考えていきたいと思います.つまり,力の和が$0$です.このとき,重心加速度は$0$になります.
重心加速度が$0$なので,重心の速度の変化は$0$です.つまり,衝突後も重心は$v_{\rm G}=\dfrac{m}{M+m}v_{0}$の速度で等速度運動します.
質量$m_{1}$,$m_{2}$の物体の重心の加速度を$a_{\rm G}$とする.2つの物体にはたらいている力をそれぞれ$F_{1}$,$F_{2}$とすると,次の式が成り立つ.
$(m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$
衝突前の重心からみた速度

衝突前の重心からみた物体A,Bそれぞれの速度を求めていきます.
ちなみに,相対速度についてはこちらの記事で解説しています.
★ 衝突前の重心からみたAの速度
$v_{0}-v_{\rm G}=v_{0}-\dfrac{m}{M+m}v_{0}=\dfrac{M}{M+m}v_{0}$ $\cdots (\ast)$
★ 衝突後の重心からみたBの速度
$0-v_{0}=-\dfrac{m}{M+m}v_{0}$ $\cdots (2\ast)$

ちなみに,重心からみた運動量の和は
$m\times \dfrac{M}{M+m}+M\times \left(-\dfrac{m}{M+m}\right)=0$
となっているね.(重心からみた運動量の和が$0$になることは下の記事で確認してください.)
衝突後の重心からみた速度のベクトル図
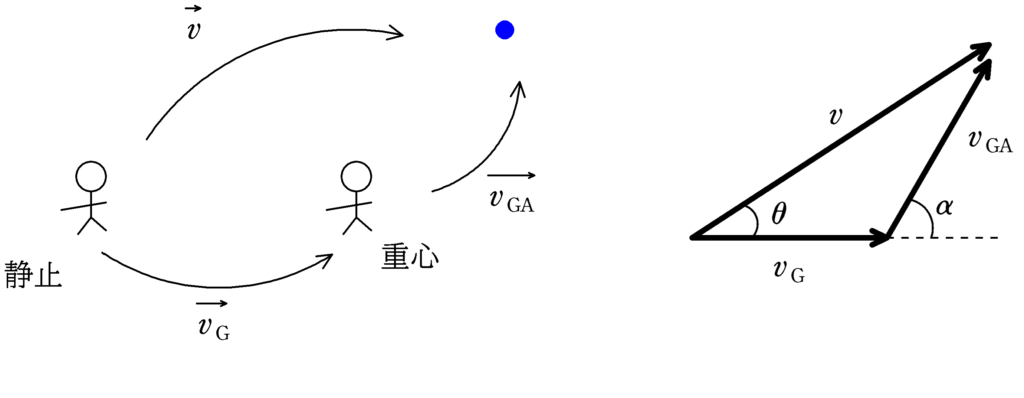

ここから衝突後の話です.
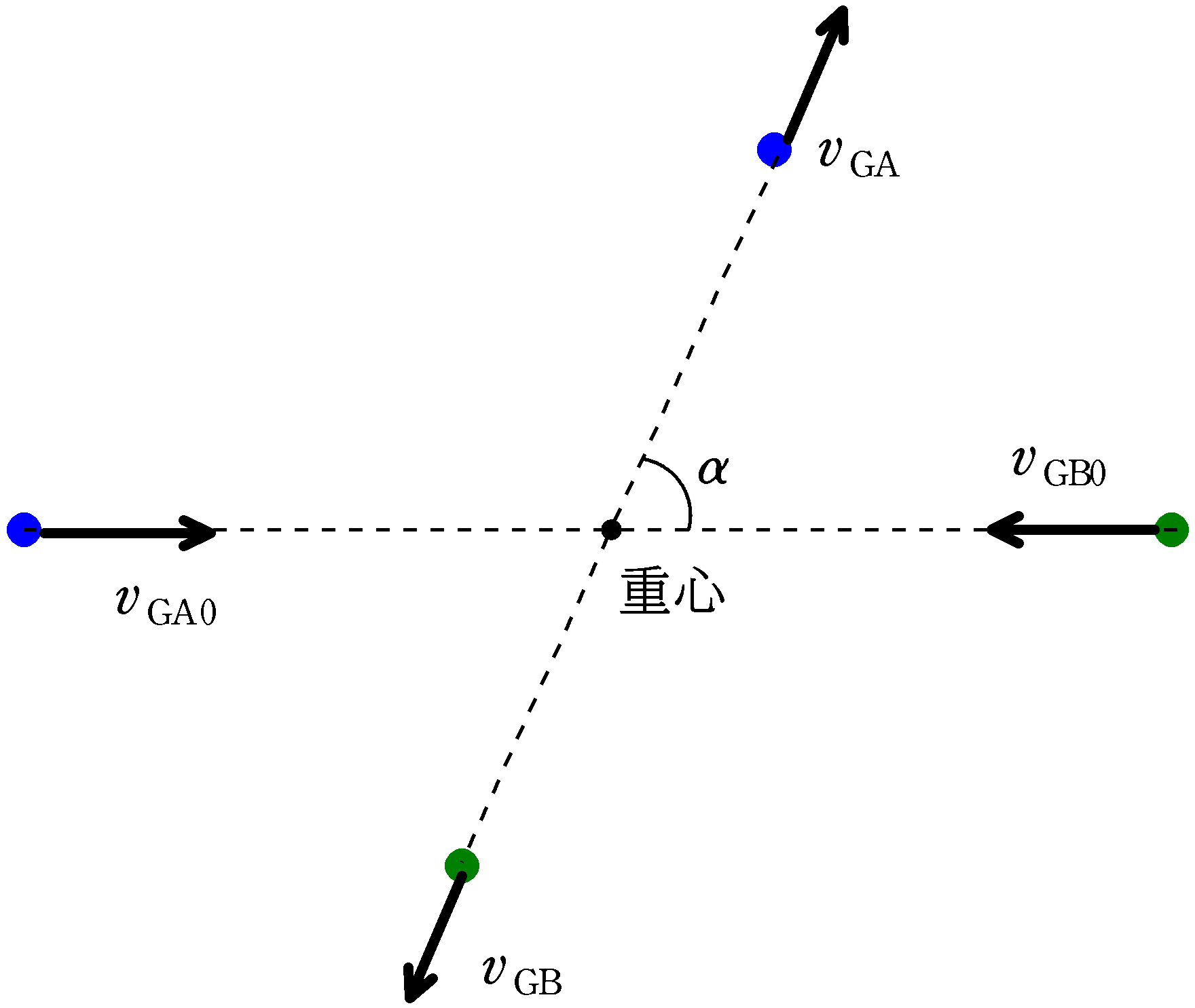
静止した人からみた物体Aの速度を$\vec{v}$,静止した人からみた重心の速度を$\vec{v_{\rm G}}$,重心からみた物体Aの速度を$\vec{v_{\rm GA}}$とします.それぞれの速さは$v,v_{\rm G},v_{\rm GA}$です.
ベクトルの加法の定義から,右上図のような閉三角形ができます.
重心からみた衝突後のAの速度は右方向より角度$\alpha$としましょう.
重心からみた運動量の和が0であることを利用する.

同じように,物体Bも閉三角形をかくことができます.
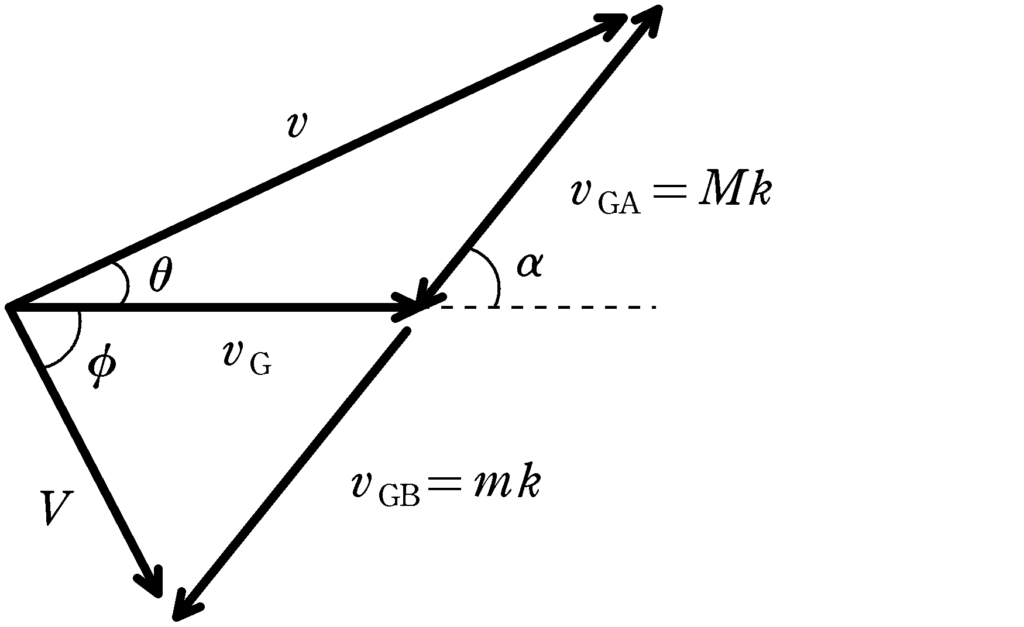

重心からみた物体Bの速度は重心からみた物体Aの速度と真反対と決めちゃっていいの?

重心からみた運動量の和が$0$なので
$m\vec{v_{\rm GA}}+M\vec{v_{\rm GB}}=\vec{0}$
となります.つまり,
$\vec{v_{\rm GB}}=-\dfrac{m}{M}\vec{v_{\rm GA}}$
なので,速度が真反対になるわけです.
そして,この関係を用いて,$v_{\rm GA}$を$Mk$をおくと
$v_{\rm GB}=\dfrac{m}{M}\times Mk=mk$
となり,正の比例定数$k$($v_{\rm GA}$,$v_{\rm GB}$が速度の大きさだから)を用いて簡単に表現できます.
余弦定理
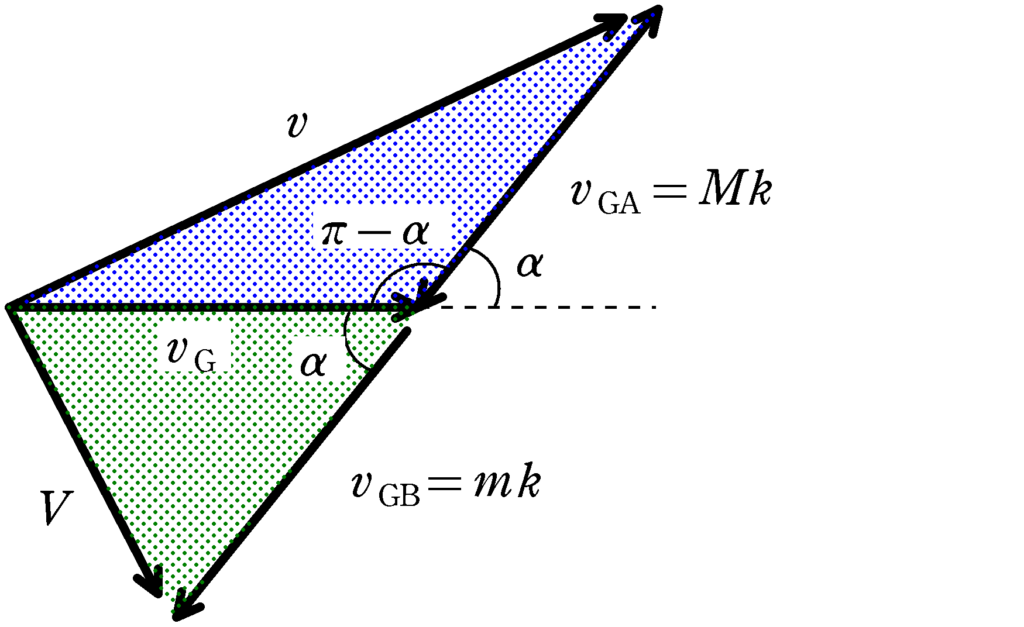

次に上の青の部分と緑の部分それぞれについて,余弦定理の式を立ててみましょう.
★ 余弦定理
青の三角形
$\eqalign{v^{2}&=v_{\rm G}^{2}+(Mk)^{2}-2v_{\rm G}\cdot (Mk)\cos(\pi-\alpha)\\&=v_{\rm G}^{2}+M^{2}k^{2}+2Mkv_{\rm G}\cos\alpha} \cdots (3\ast)$
緑の三角形
$\eqalign{V^{2}&=v_{\rm G}^{2}+(mk)^{2}-2v_{\rm G}\cdot (mk)\cos\alpha\\&=v_{\rm G}^{2}+m^{2}k^{2}-2mkv_{\rm G}\cos\alpha} \cdots (4\ast)$
力学的エネルギー保存則


弾性衝突を考えているので,力学的エネルギーが保存します.
★ 力学的エネルギー保存則
$\cancel{\dfrac{1}{2}}mv_{0}^{2}=\cancel{\dfrac{1}{2}}mv^{2}+\cancel{\dfrac{1}{2}}MV^{2}$
$(3\ast),(4\ast)$を代入して$k$を求める.
$\eqalign{mv_{0}^{2}&=m\{v_{\rm G}^{2}+M^{2}k^{2}+2Mkv_{\rm G}\cos\alpha\}+M(v_{\rm G}^{2}+m^{2}k^{2}-2mkv_{\rm G}\cos\alpha)\cr mv_{0}^{2}&=mv_{\rm G}^{2}+mM^{2}k^{2}+\cancel{2Mmkv_{\rm G}\cos\alpha}+Mv_{\rm G}^{2}+Mm^{2}k^{2}\cancel{-2Mmkv_{\rm G}\cos\alpha}}$
$\therefore\,\,Mm(M+m)k^{2}+(M+m)v_{\rm G}^{2}=mv_{0}^{2}$
$v_{\rm G}=\dfrac{m}{M+m}v_{0}$を代入すると
$M\bcancel{m}(M+m)k^{2}+\cancel{(M+m)}\cdot \dfrac{m^{\bcancel{2}}v_{0}^{2}}{(M+m)^{\cancel{2}}}=\bcancel{m}v_{0}^{2}$
$\eqalign{\therefore\,\,M(M+m)k^{2}&=v_{0}^{2}\left(1-\dfrac{m}{M+m}\right)\\&=\dfrac{M}{M+m}v_{0}^{2}}$
$k^{2}=\left(\dfrac{v_{0}}{M+m}\right)^{2}$であり,$k>0$であるから,
$k=\dfrac{v_{0}}{M+m}$

したがって
$v_{\rm GA}=Mk=\dfrac{M}{M+m}v_{0}$
$v_{\rm GB}=mk=\dfrac{m}{M+m}v_{0}$
となります.

$(\ast)$,$(2\ast)$より,衝突前の重心からみたA,Bそれぞれの速度の大きさは
$\dfrac{M}{M+m}v_{0}$,$\dfrac{m}{M+m}v_{0}$
だったから,確かに衝突前後で重心からみたそれぞれの物体の速さは変化していないね!



コメント