次のことに当てはまる人はこの記事を読むことをおすすめします.
- 速度の向きを意識して計算ができないので,計算がぐちゃぐちゃになっている.
- 2次元運動になると,何がなんだかわからない.
- そもそも言葉の意味がわかない.
Aに対するBの相対速度とは
相対速度の問題は言葉でやられてしまう人が大半かと思います.問題文で
“物体Aに対する物体Bの相対速度を求めよ.”
と書かれていたとき,これだけだと何がなんだかわかりません.この文章は次のように言い換えましょう.
“物体AからみたときのBの速度を求めよ.”
“対する”→“からみた”と言い換えると気持ちが楽になります.
速度は誰から見るかによって速度が違うんです.たとえば,歩いている人から車をみるのと,車Aに乗っている人から見たほかの車Bの速度は違います.もし,車Aと車Bが同じ速度の向きであれば,車Bはゆっくり動いているように見えます.こどもの頃不思議だなーと思ってよく見ていました.
一直線上の相対速度(1次元)
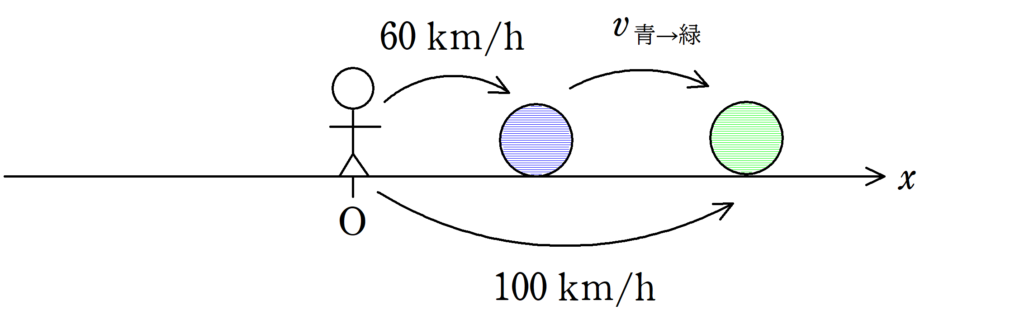
上図のような座標を設定する.原点で静止している人からみて青の物体の速度$v_{青}$は$x$軸の正の向きに$60 \rm{km/h}$,つまり$v_{青}=60 \rm{km/h}$である.また,原点で静止している人からみて緑の物体の速度$v_{緑}$は$x$軸の正の向きに$100 \rm{km/h}$,つまり$v_{緑}=100 \rm{km/h}$である.このとき,青の物体に対する緑の物体の相対速度$v_{青\rightarrow 緑}$を求めよ.
<解答>
つまり,”青の物体からみた緑の物体の速度”です.これは直観的にすぐ計算できるでしょう.答は$x$軸の正の方向に$40 \rm{km/h}$です.
$v_{青}$と$v_{緑}$と$v_{青\rightarrow 緑}$には次の関係が成り立っています.
$v_{青}$$+$$v_{青\rightarrow 緑}$$=$$v_{緑}$ $\dots (\ast)$
これは経験則です.次のようなイメージをもちましょう.
青を経由して緑にいく矢印の和は,直接緑いく矢印と等しい
これはまさにベクトルです.
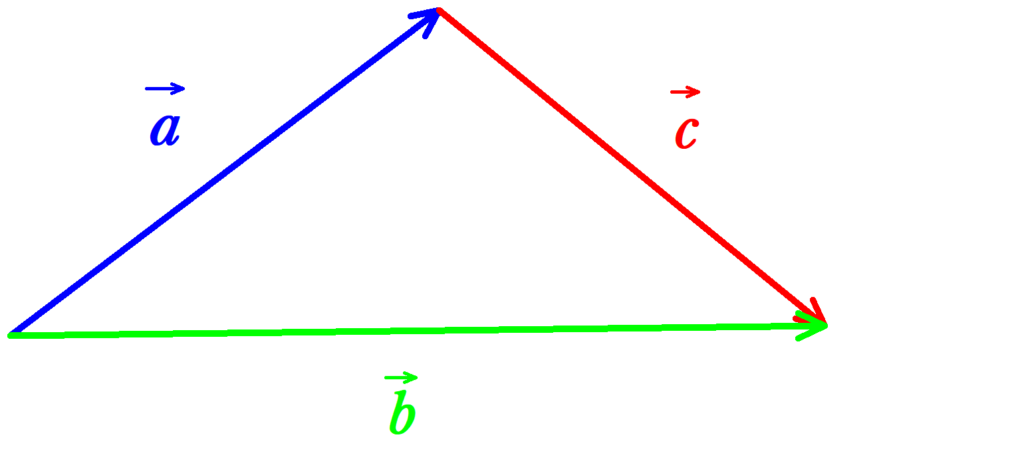
上図では$\vec{a}$$+$$\vec{c}$$=$$\vec{b}$の関係があります.これもスタートから経由する矢印の和は直接ゴールにいく矢印と等しいという関係になっていますね.
さて,$(\ast)$に,$v_{青}=60\rm{km/h}$と$v_{緑}=100\rm{km/h}$を代入しましょう.
$60$$+$$v_{青\rightarrow 緑}$$=$$100$ $\therefore$ $v_{青\rightarrow 緑}=40 \rm{km/h}$
このようにして,ベクトル意識すると,より複雑な運動でも対応ができます.では,次の問題にいきましょう.
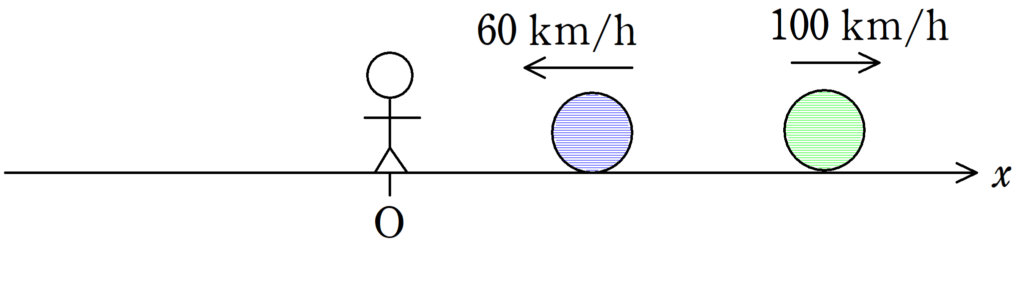
上図のような座標を設定する.原点で静止している人からみて青の物体は$x$軸の負の向きに$60 \rm{km/h}$の速度をもっている.また,原点で静止している人からみて緑の物体は度$v_{緑}$は$x$軸の正の向きに$100 \rm{km/h}$の速度をもっている.このとき,緑の物体に対する青の物体の相対速度を求めよ.
<解答>
こちらも直観的にできるかと思います.答えは$x$軸の負の向きに速さ$160 \rm{km/h}$です.では,ベクトルをつかって解きましょう.
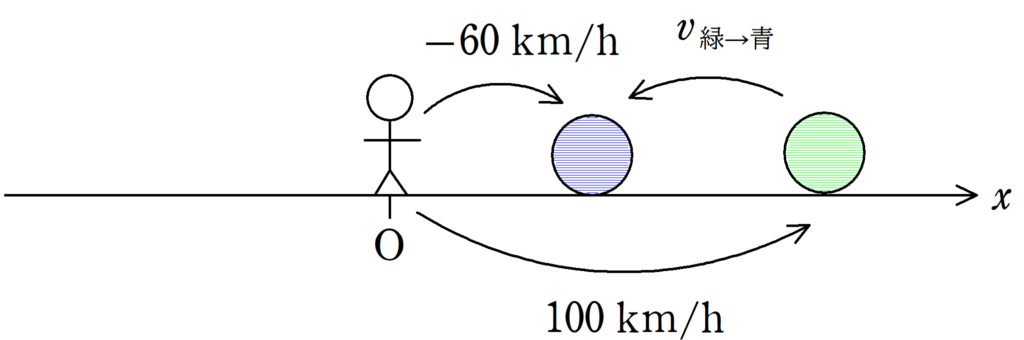
青い物体は$x$軸の負の向きの速度をもっているので,$v_{青}=-60 \rm{km/h}$です.一方,緑の物体の速度は$v_{緑}=100 \rm{km/h}$となります.今度は”緑に対する青の物体の速度”なので,”緑からみた青の物体の速度”を求めることになります.だから,”緑”から”青”に向かって矢印をひきましょう.以上を考慮すると,上図のようになります.
経由した矢印と直接の矢印の関係は次のようになります.
$v_{緑}$$+$$v_{緑\rightarrow 青}$$=$$v_{青}$
したがって,
$100+$$v_{緑\rightarrow 青}$$=-60$ $\therefore$ $v_{緑\rightarrow 青}=-160 \rm{km/h}$
このように,$+,-$の情報をいれればきちんと解くことができます.
2次元運動
1次元運動では直観的にできても,2次元運動になった途端にできくなる人います.次の問題を考えてみましょう.
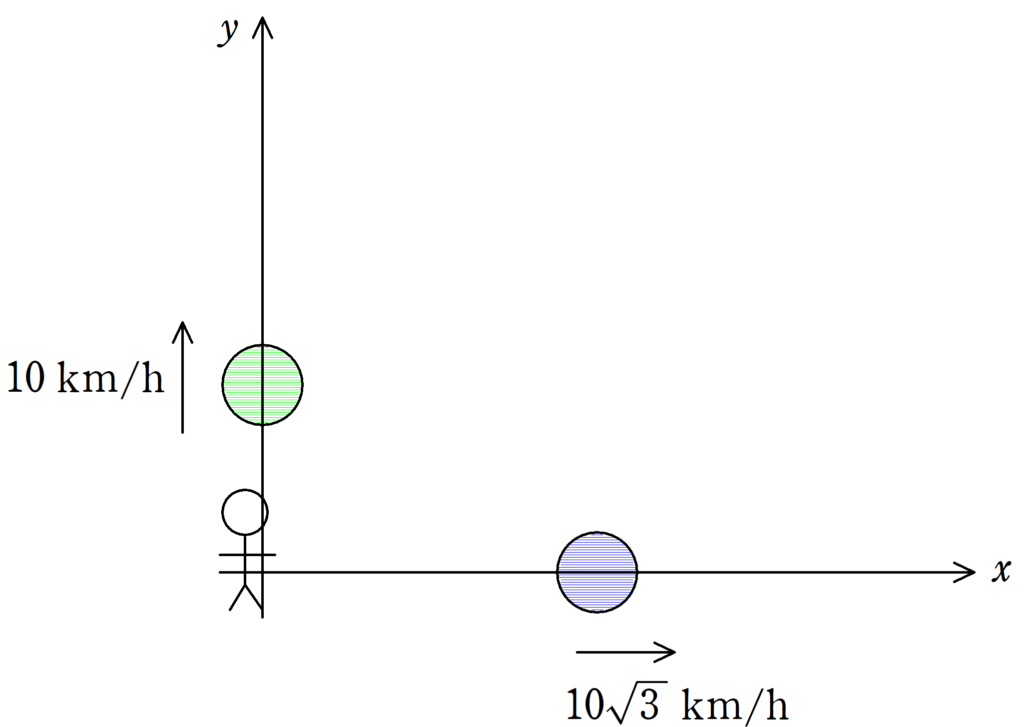
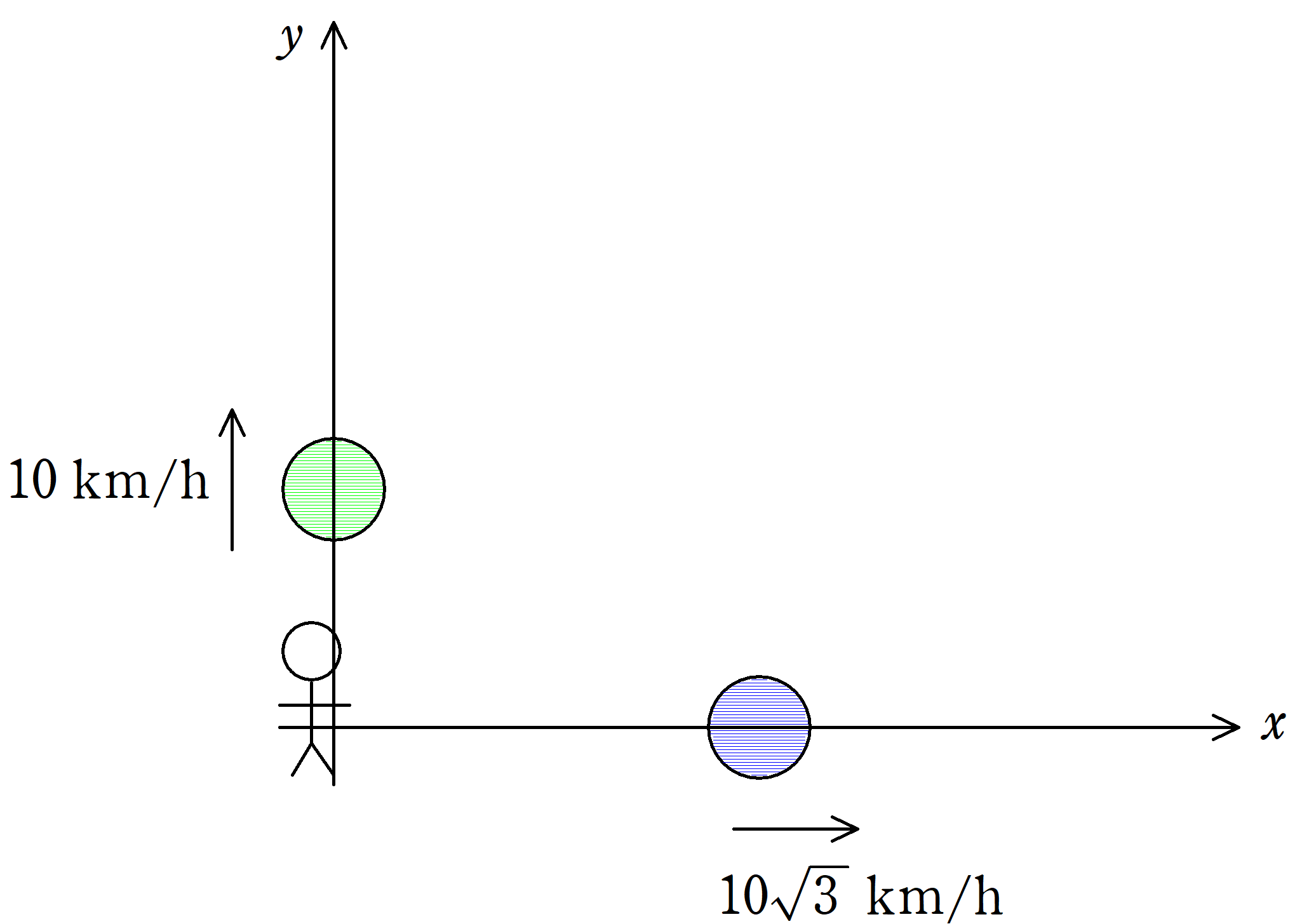
上図のように$xy$直交座標がとられている.原点で静止した人からみて,青の物体は$x$軸の正の向きに速さ$10\sqrt{3} \rm{km/h}$で運動しており,緑の物体は$y$軸の正の向きに速さ$10 \rm{km/h}$で運動している.このとき,緑の物体に対する青の物体の相対速度の速さと向きを答えよ.
<解答>
2次元運動のときは速度を
$(x方向の速度,y方向の速度)$
と表すとよいでしょう.
このような表現をすると,$v_{青}=(10\sqrt{3},0)$,$v_{緑}=(0,10)$となります.緑から青に矢印を引いて
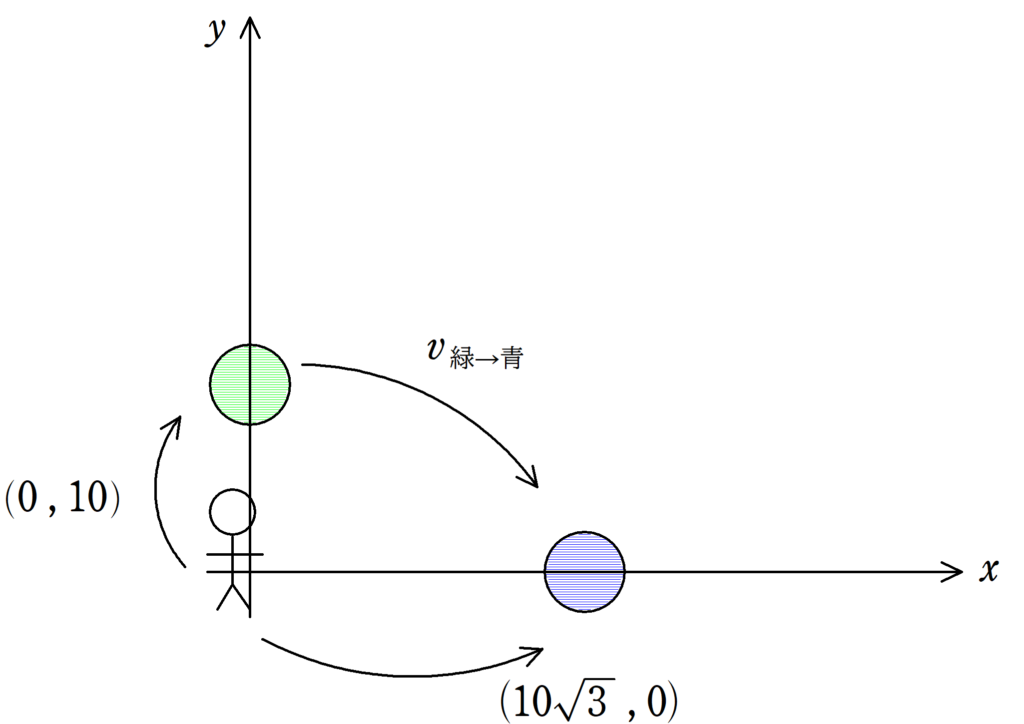
すると,経由した矢印と直接の矢印は次のような関係になります.
$v_{緑}$$+$$v_{緑\rightarrow青}$$=$$v_{青}$ $\therefore$ $v_{緑\rightarrow 青}$$=$$v_{青}$$-$$v_{緑}$
ここに,$v_{青}=(10\sqrt{3},0)$,$v_{緑}=(0,10)$を代入すると
$v_{緑\rightarrow 青}=(10\sqrt{3},0)-(0,10)=(10\sqrt{3},-10)$
以上より,緑の物体からみた青の物体の速度は,$x$方向に$10\sqrt{3}$,$y$方向に$-10$であることがわかります.図示すると下のようになります.
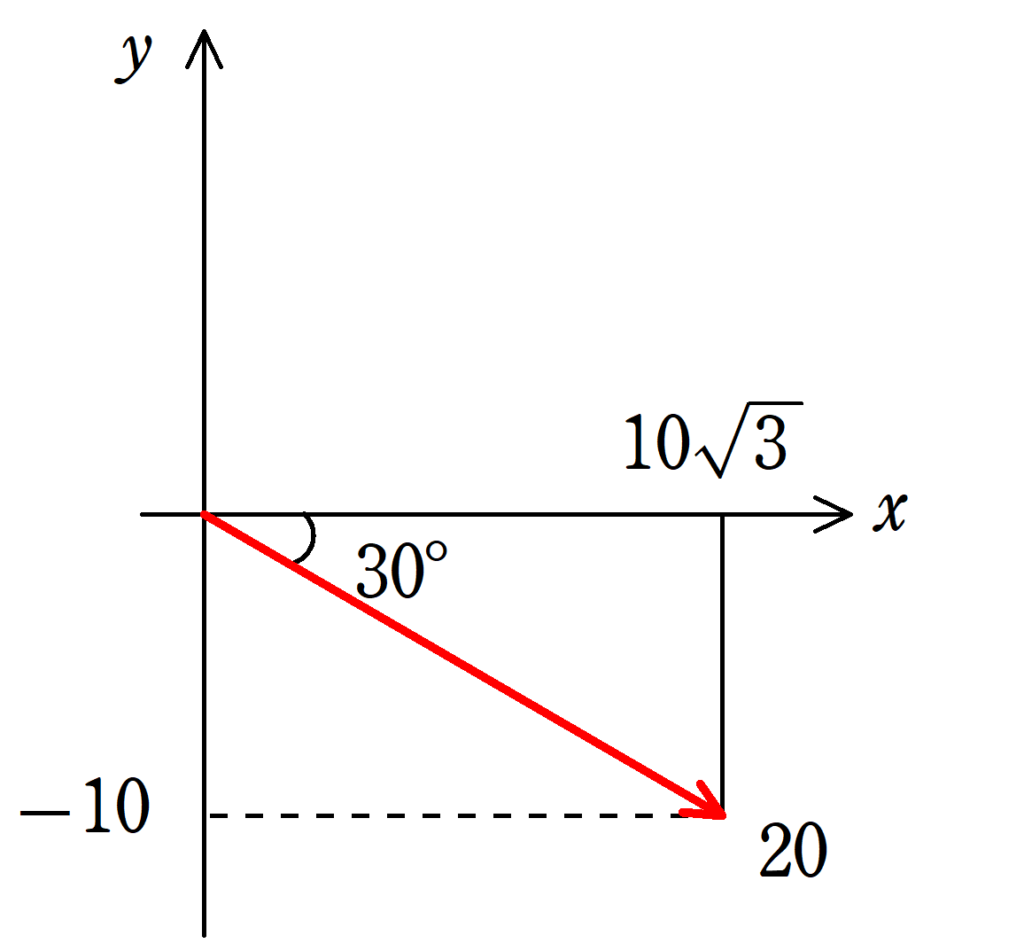
三平方の定理を利用して速さを求めると,$20\rm{km/h}$となります.その方向は$x$軸の正の方向か時計まわりに30°の方向です.
まとめ
- “Aに対するBの相対速度“は”A”からみたBの速度“のことである.
- 相対速度の計算は,”経由した矢印=直接の矢印“でベクトル計算をする.その際,軸の向きを決め,+,-の情報を入れる.2次元運動の場合は$(x方向の速度,y方向の速度)$と表示する.
相対速度は2つ以上の物体が動くときに必須の計算となります.確実に計算ができるようにしましょう.



コメント
[…] […]
[…] […]
[…] 確実に計算する相対速度 […]
[…] […]