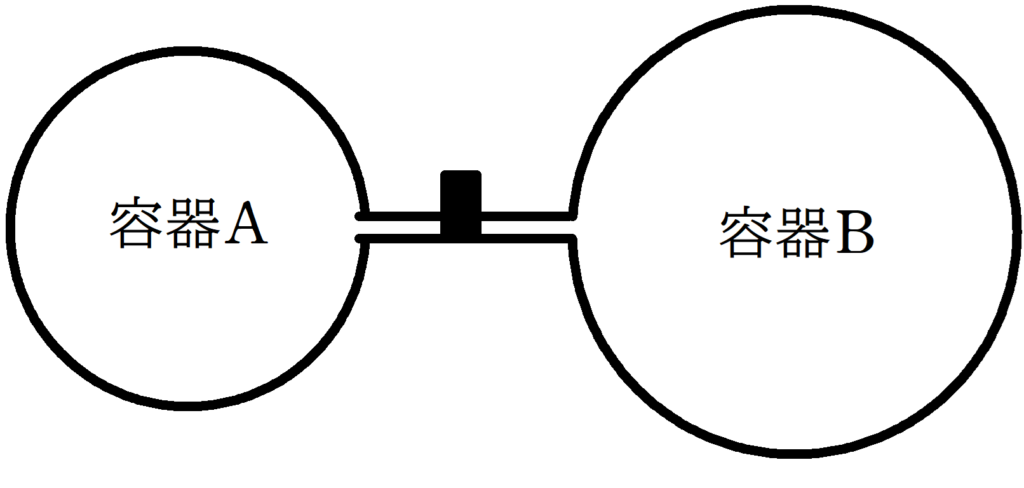
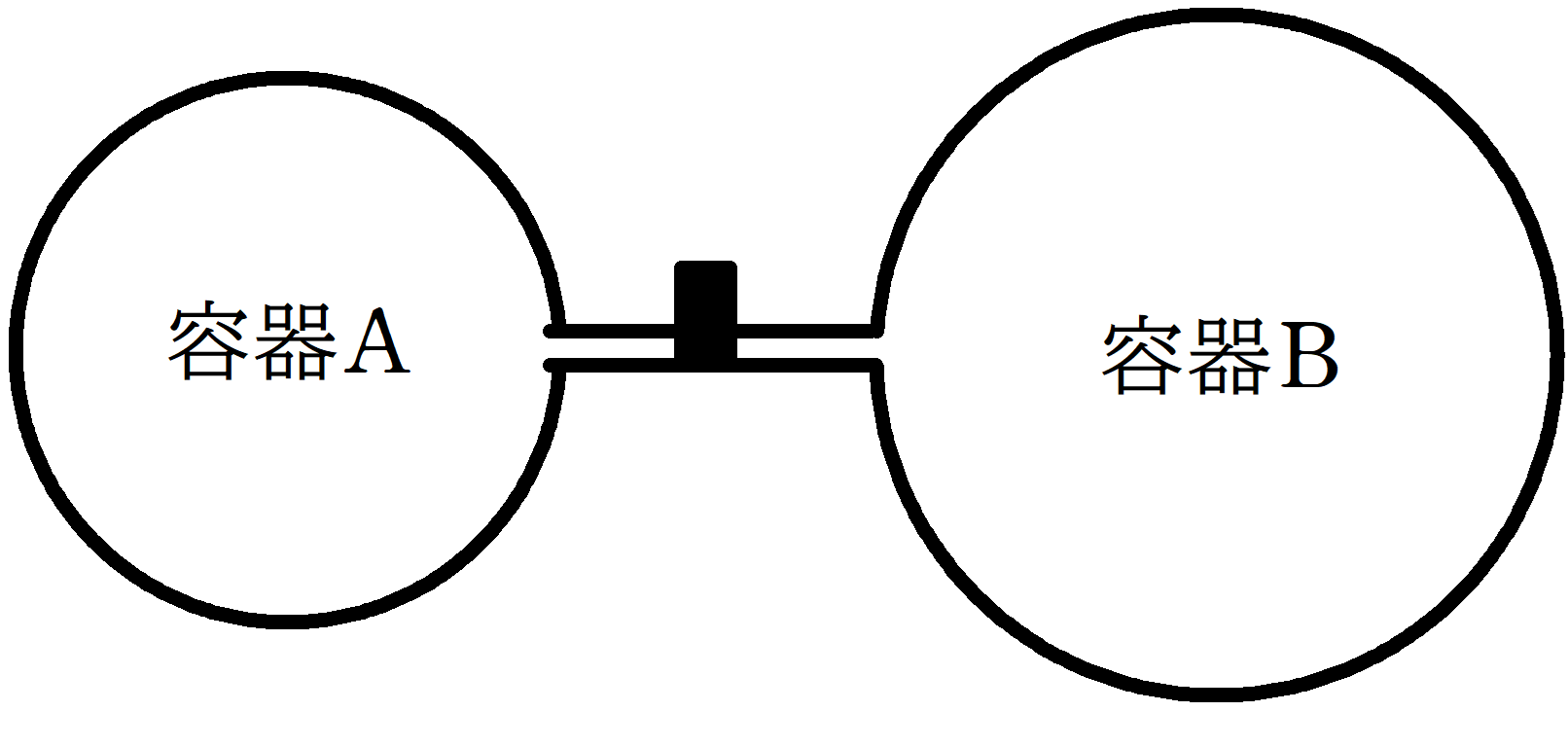
断熱材でできた容器A,容器B,コック,細管が図のようにつながれている.はじめコックが閉じている状態で,容器Aには圧力$P_{0}$,体積$V_{0}$,絶対温度が$T_{0}$の単原子分子理想気体が,容器Bには,圧力$2P_{0}$,体積$3V_{0}$,絶対温度$T_{0}$の二原子分子理想気体が封入されている.気体定数を$R$とすると,単原子分子気体の定積モル比熱は$\dfrac{3}{2}R$,二原子分子気体の定積モル比熱は$\dfrac{5}{2}R$であるとする.
ある時刻でコックをゆっくと開き,十分時間が経つと,気体が混合され,気体の圧力は$P$,絶対温度は$T$となった.このとき,$P,T$をそれぞれ$P?{0},T_{0}$から必要なものを用いて表せ.
<解答>

こちらでは,単原子分子同士の気体の混合でしたが,今回は単原子分子気体と二原子分子気体の混合問題です.
前回と同様に,気体の混合の問題では
- 物質量保存則
- 熱力学第一法則(容器が変形しなくて,断熱されているので,実質内部エネルギー保存)
を立てます.
容器Aにある気体の物質量$n_{\rm A}$と容器B内にある物質量$n_{\rm B}$はそれぞれ
$n_{\rm A}=\dfrac{P_{0}V_{0}}{3RT_{0}}$,$n_{\rm B}=\dfrac{6P_{0}V_{0}}{RT_{0}}$
であり,混合後の物質量の和は
$\dfrac{P\times 4V_{0}}{RT}=\dfrac{4PV_{0}}{RT}$
なので
★ 物質量保存則
$\dfrac{P_{0}\cancel{V_{0}}}{3\bcancel{R}T_{0}}+\dfrac{6P_{0}\cancel{V_{0}}}{\bcancel{R}T_{0}}=\dfrac{4P\cancel{V_{0}}}{\bcancel{R}T}$
$\therefore\,\, \dfrac{P}{T}=\dfrac{19P_{0}}{12T_{0}}$ $\cdots (\ast)$

さらに,単原子分子理想気体の内部エネルギーの表式は$\dfrac{3}{2}nRT$なのに対して,二原子分子理想気体は$\dfrac{5}{2}nRT$であるから
★ 内部エネルギー保存則
$\dfrac{3}{2}\times n_{\rm A}R\times 3T_{0}+\dfrac{5}{2}\times n_{\rm B}R\times T_{0}=\dfrac{3}{2}\times n_{\rm A}RT+\dfrac{5}{2}\times n_{\rm B}RT$
$n_{\rm A}=\dfrac{P_{0}V_{0}}{3RT_{0}}$,$n_{\rm B}=\dfrac{6P_{0}V_{0}}{RT_{0}}$を代入して,$T$について解くと
$\dfrac{3}{2}\times \dfrac{\bcancel{P_{0}V_{0}}}{\cancel{3RT_{0}}}\times \cancel{R\times 3T_{0}}+\dfrac{5}{2}\times \dfrac{6\bcancel{P_{0}V_{0}}}{\cancel{RT_{0}}}\times \cancel{R\times T_{0}}=\dfrac{3}{2}\times \dfrac{\bcancel{P_{0}V_{0}}}{3\cancel{R}T_{0}}\times \cancel{R}T+\dfrac{5}{2}\times \dfrac{6\bcancel{P_{0}V_{0}}}{\cancel{R}T_{0}}\times \cancel{R}T$
$\therefore\,\, \dfrac{3}{2}+15=\dfrac{T}{2T_{0}}+\dfrac{15T}{T_{0}}$
$\therefore\,\, T=\dfrac{33}{31}T_{0}$ (答)
これを$(\ast)$に代入して整理すると
$P=\dfrac{19P_{0}}{12T_{0}}\times \dfrac{33}{31}T_{0}$
$\therefore\,\, P=\dfrac{19\times 11}{4\times 31}P_{0}=\dfrac{209}{124}P_{0}$ (答)

コメント
[…] […]