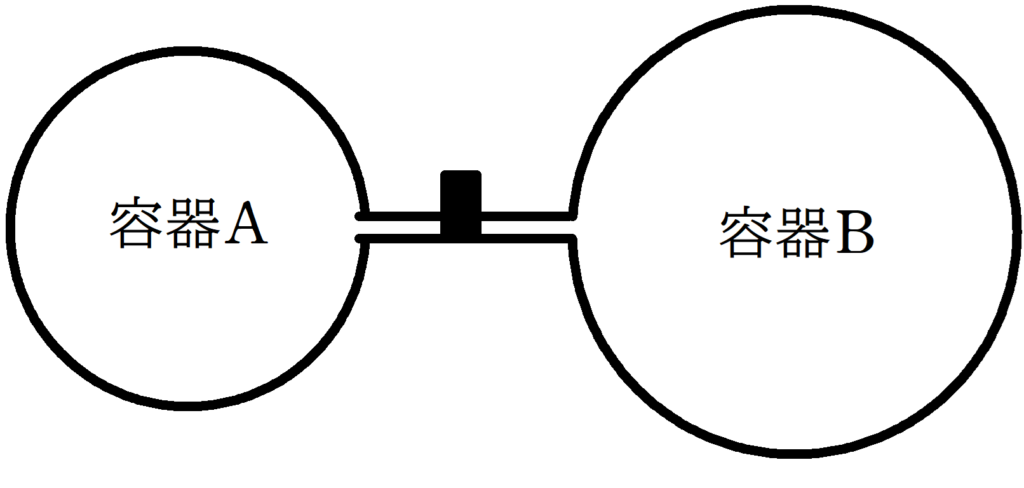
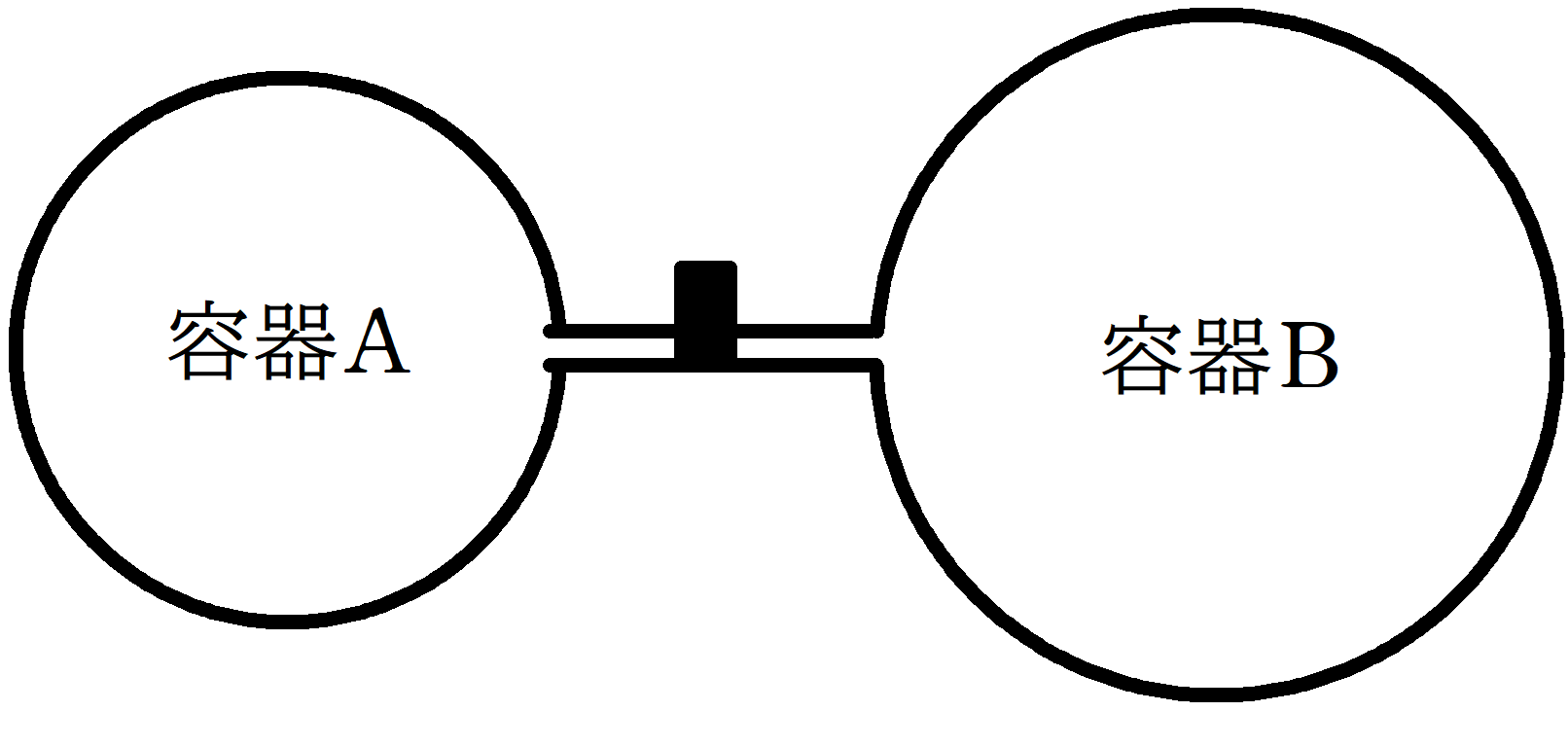
断熱材でできた容器A,容器B,コック,細管が図のようにつながれている.はじめコックが閉じている状態で,容器A,Bともに圧力$P_{0}$,体積$V_{0}$,絶対温度が$T_{0}$の単原子分子理想気体が封入されている.
容器A , Bにはそれぞれ温度調節器が備え付けられており,容器A側の気体と容器B側の気体を別々の温度に保つことができる.
コックを開いて,容器A側の絶対温度を$T_{0}$に保ち,容器B側の絶対温度を$2T_{0}$に保ったとき,容器A , B内の気体の圧力$P_{1}$を$P_{0}$を用いて表せ.
<解答>

今回は熱力学第一法則を立てることがでいません!
容器A,B内の温度調節器によって気体に熱を与えたり,吸収したりしているのですが,その具体的な熱量が問題に与えられていないので,計算ができないんです.
そこで,物質量保存の式を立てましょう.
化学反応は起こらないと,前後での分子の数は変化しません.
圧力を$p$,体積を$V$,物質量を$n$,気体定数を$R$,絶対温度を$T$とすると,理想気体の状態方程式を変形すると次のようになります.
$pV=nRT$
$\therefore n=\dfrac{pV}{RT}$
★ 物質量保存則
気体定数を$R$とすると
$\eqalign{\dfrac{P_{0}V_{0}}{RT_{0}}+\dfrac{P_{0}V_{0}}{RT_{0}}&=\dfrac{P_{1}V_{0}}{RT_{0}}+\dfrac{P_{1}V_{0}}{R\cdot (2T_{0})}\cr \dfrac{3P_{1}V_{0}}{2RT_{0}}&=\dfrac{2P_{0}V_{0}}{RT_{0}}\cr P_{1}&=\dfrac{4}{3}P_{0}}$

ということで,$P_{1}=\dfrac{4}{3}P_{0}$(答)となります.

コメント