<解答>
水平方向,鉛直方向それぞれの運動を考えるところがポイントです.
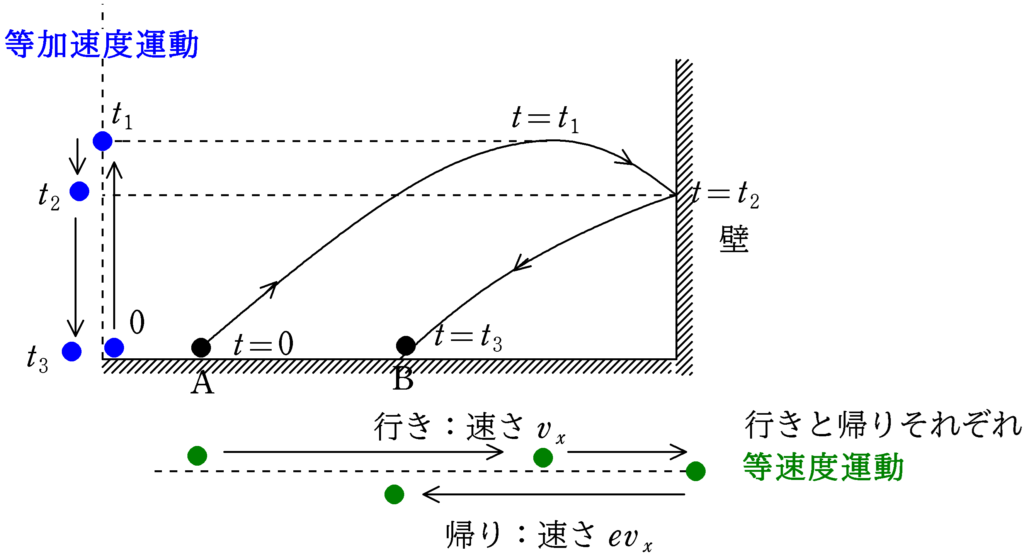
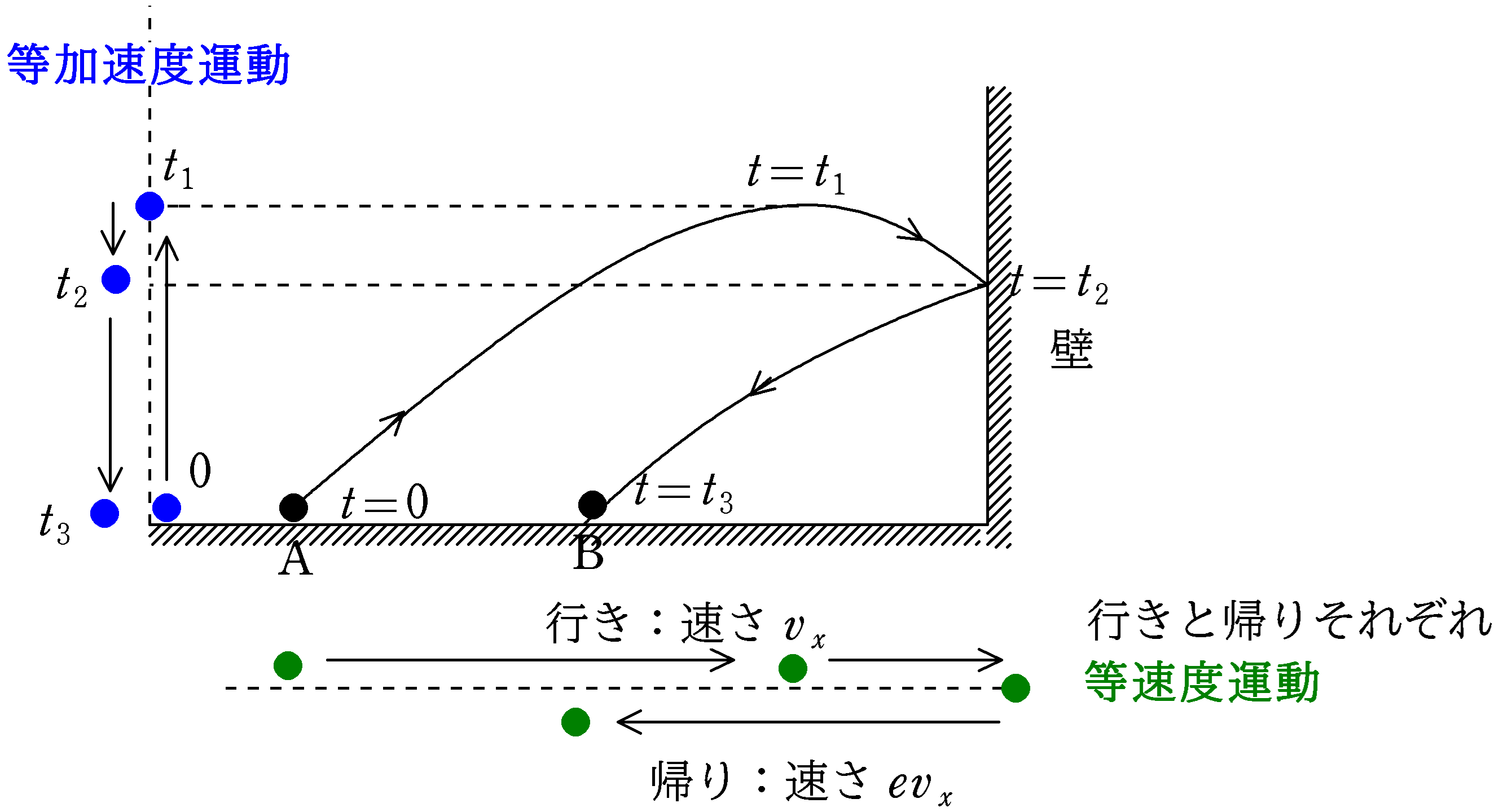
途中で衝突しているものの,衝突によって鉛直方向の外力は受けていない.つまり,力積は$0$なので,衝突による運動量の変化はなし.これは,壁の衝突がないときの斜方投射と同じ運動をすることを意味する.
壁がないときの斜方投射で初速を与えてから再び水平面に帰ってくるまでの時間を$T$とすると,水平方向は等速度運動をしているので,水平速度を$v_{x}$として
$v_{x}T=l$ $\therefore T=\dfrac{l}{v_{x}}\cdots (\ast)$
が成り立つ.
先ほど考えたように,壁との衝突がある場合についても鉛直方向の運動が同じなので,A点で初速を与えてから壁と衝突し,B点に達するまでの時間は同じく$T$である.
A点から壁と衝突するまでの時間を$t_{\rm A}$とすると,水平方向の変位と速度の時間の関係より
$l_{\rm A}=v_{x}t_{\rm A}$ $\therefore t_{\rm A}=\dfrac{l_{\rm A}}{v_{x}}\cdots (2\ast)$
衝突後の水平速度の大きさは反発係数$e$倍になり,$ev_{x}$となる.壁と衝突してからBに達するまの時間を$t_{\rm B}$とすると,水平方向の変位と速度の時間の関係より,
$l_{\rm B}=ev_{x}t_{\rm B}$ $\therefore t_{\rm B}=\dfrac{l_{\rm B}}{ev_{x}}\cdots (3\ast)$
$T=t_{1}+t_{2}$なので,$(\ast)$~$(3\ast)$より
$\dfrac{l}{\cancel{v_{x}}}=\dfrac{l_{\rm A}}{\cancel{v_{x}}}+\dfrac{l_{\rm B}}{e\cancel{v_{x}}}$
$\therefore \dfrac{l_{\rm B}}{e}=l-l_{\rm A}$ $\therefore\,\, e=\dfrac{l_{\rm B}}{l-l_{\rm A}}$(答)


コメント