
NEKO
コンデンサーに蓄えられている電荷を$q$として,流れる電流を$i$としたとき,
$i=\dfrac{\varDelta q}{\varDelta t}$
だったり
$i=-\dfrac{\varDelta q}{\varDelta t}$
だったりするけど,どちらが正しいんだろう?

PHYさん
結論をいえば,どちらも正しいです.
2つの違いの原因は,電流の正方向の定義になります.
下の2つを見てください.
コンデンサーの正電荷が蓄えられている方に入り込むように,電流の向きをとっている場合は,
$i=\dfrac{\varDelta q}{\varDelta t}$
で,コンデンサーの正電荷が蓄えられている方から出ていくような向きに,電流の向きをとっている場合は
$i=-\dfrac{\varDelta q}{\varDelta t}$
となります.
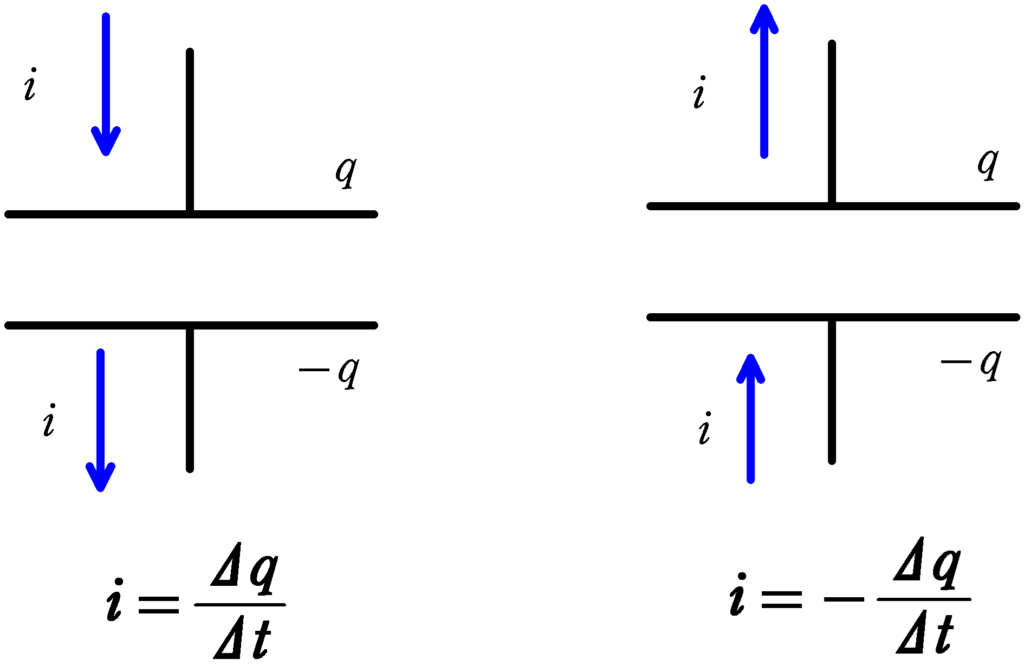

PHYさん
要するに,「-」がつくかつかないかは,両辺の符号を合わせるように調整しているんです.
たとえば,上図の左側は
$i$が正→$q$が増える→$\varDelta q>0$
になるので,左辺,右辺ともに正となります.
一方,上図の右側は
$i$が正→$q$が減る→$\varDelta q<0$
になるので,$i=\dfrac{\varDelta q}{\varDelta t}$にしてしまうと,左辺と右辺の符号が合いません.
そこで,右辺に「$-$」をつけると
$i=- \dfrac{\varDelta q}{\varDelta t}$
で左辺,右辺ともに正となり,符号が合います.

NEKO
なるほど,電流の正の向きをどちらにしたのかは確認しないとなんだね.

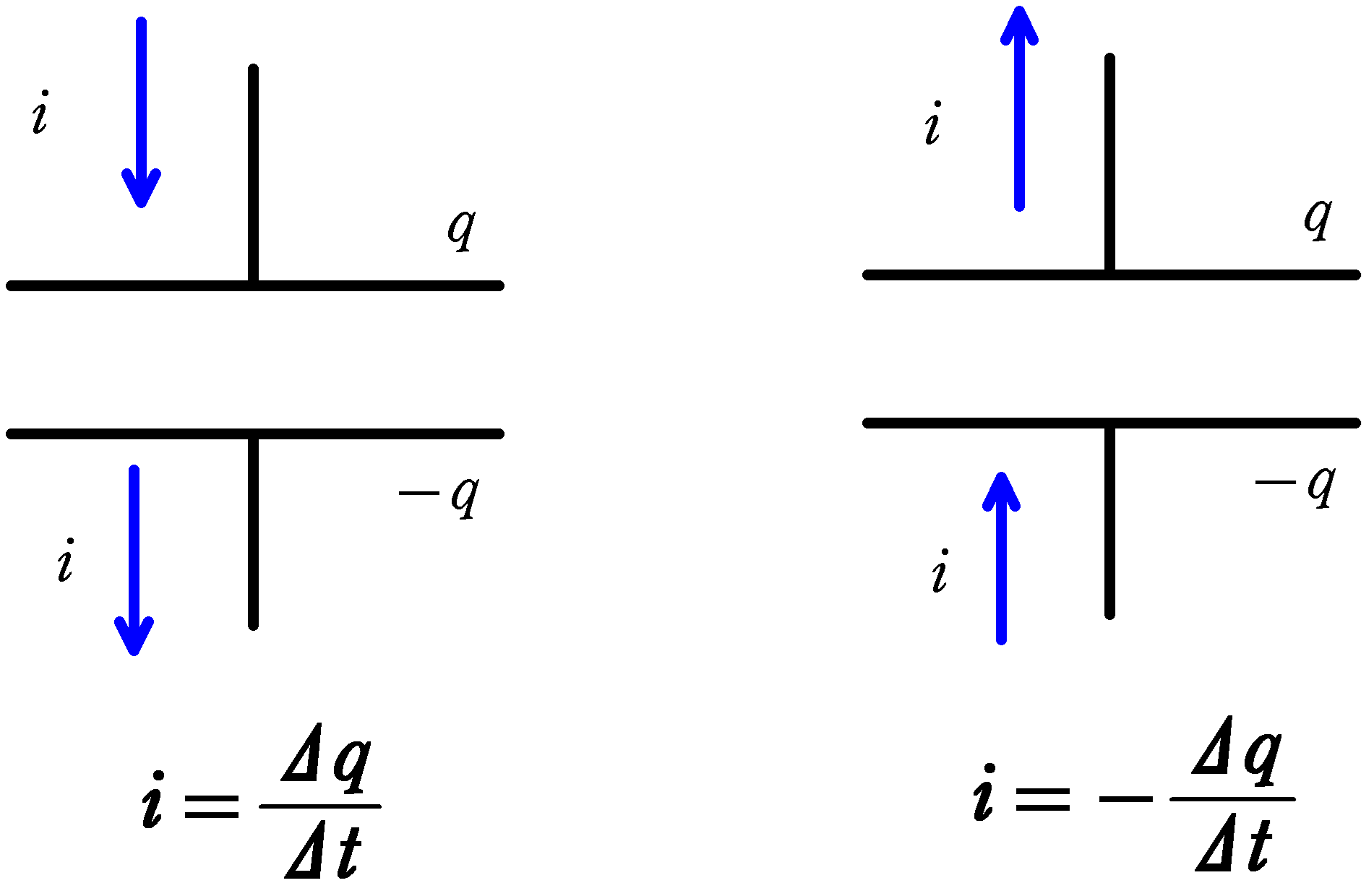
コメント