twitterの問題52　動摩擦力がする仕事（問題文をよく読んで答える）

<問題>

<解答>

問題文の

「動摩擦力の大きさは摩擦が存在する接触面の垂直抗力の大きさに比例する．」

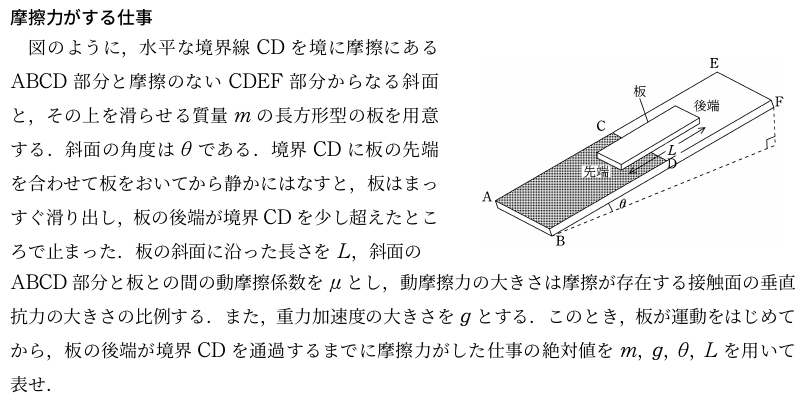
から，板が斜面ABCDにある部分の垂直抗力の大きさ$N_{1}$を求める必要があります．

斜面ABCD部分にある板の重力は，板の先端と境界線CDの距離を$x$とすると，

$\dfrac{x}{L}\times mg$

なので，これを斜面平行な方向と垂直な方向に分解して，斜面垂直方向のつり合いの式を立てると

$N_{1}=\dfrac{x}{L}mg\cos\theta$

となります．ちなみに，上のつり合いの式の対象は「板の斜面ABCDに侵入している部分」です．

すると，板の先端と境界線CDの距離が$x$のときの動摩擦力の大きさ$F$は

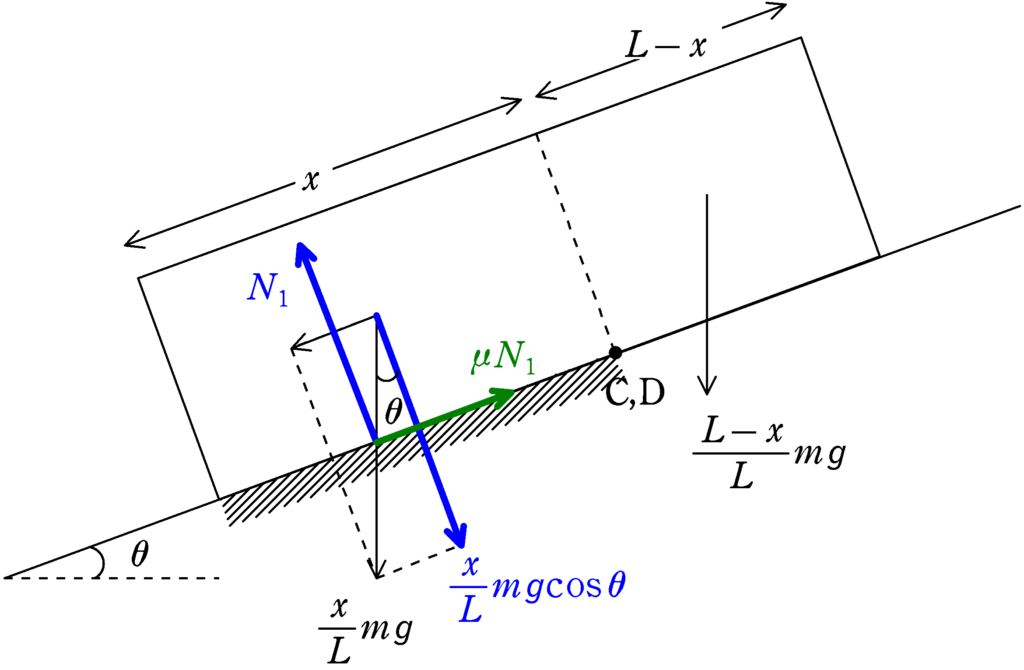
$F=\mu N_{1}=\dfrac{\mu mg\cos\theta}{L}x$

となり，$x$によって，動摩擦力の大きさ$F$が変化することがわかります．

縦軸を$F$，横軸を$x$として，グラフを書くと下図のようになります．

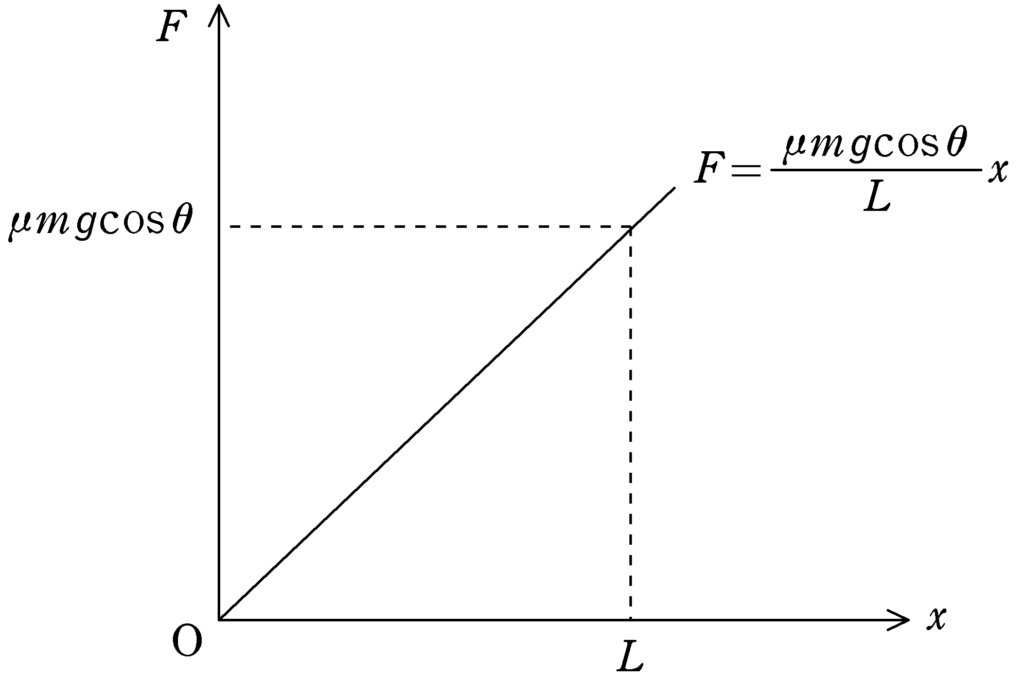
下図のように，横軸が$\varDelta x$の長方形の面積は

$F\varDelta x$

でちょうど仕事の絶対値を表しているので，$\varDelta x$を非常に小さくして足し合わせることで$x=0$～$L$までに動摩擦力がした仕事の絶対値が計算できます．

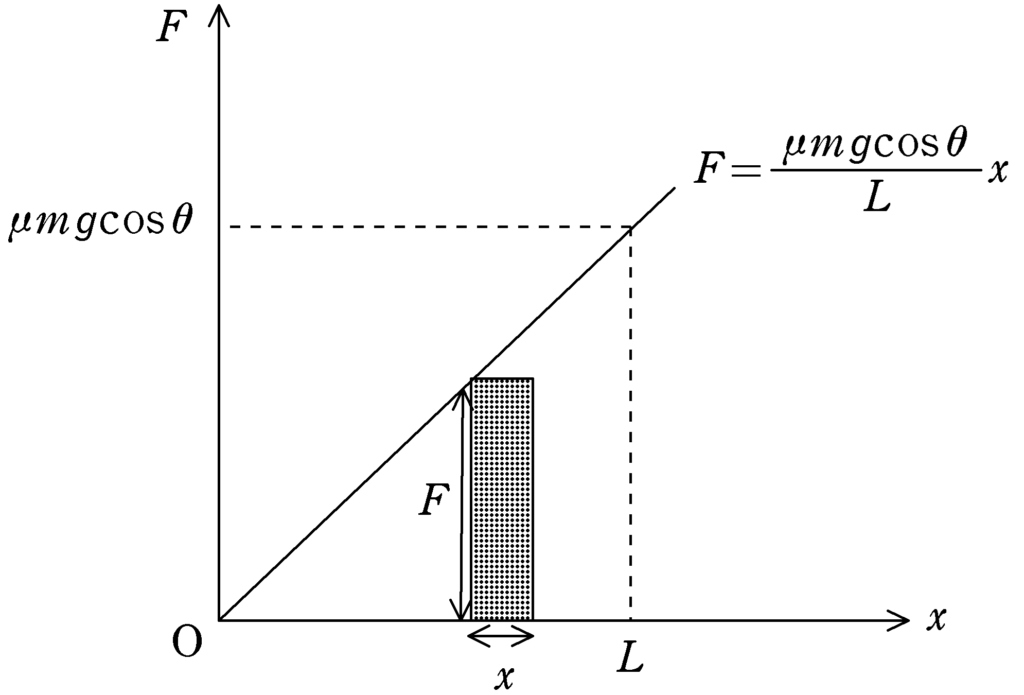
下図の直角三角形の面積を計算すると

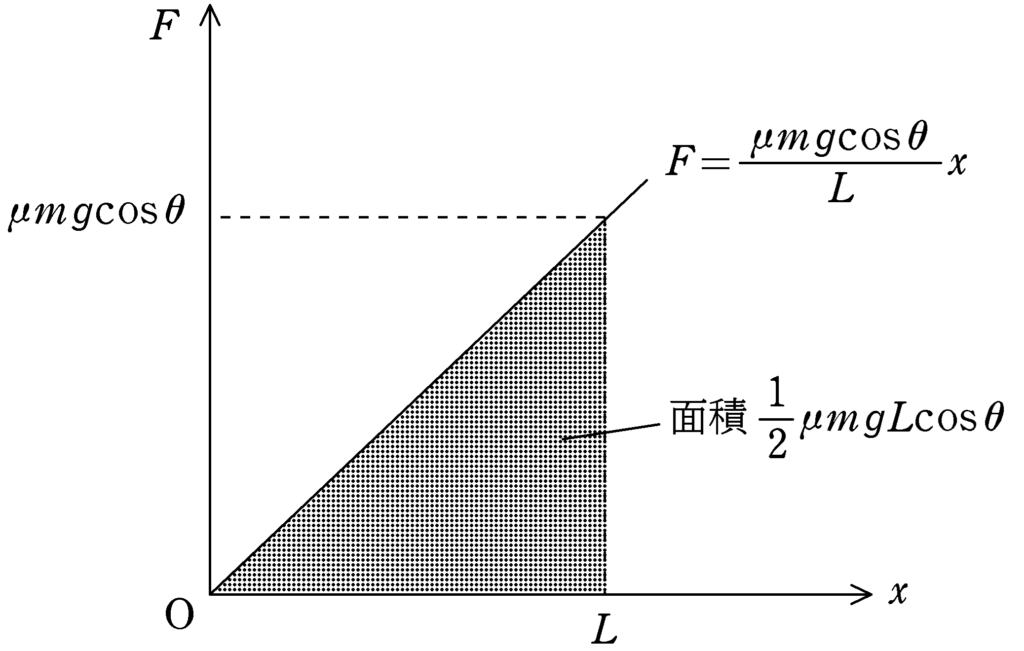
$\dfrac{1}{2}\times L\times \dfrac{\mu mg\cos\theta}{L}L=\dfrac{1}{2}\mu mgL\cos\theta$ (答)

今回は「物体が接触している面から受ける摩擦力の大きさは，摩擦がする接触面の垂直抗力の大きさに比例する」ということから計算しました．この手の問題は毎回問題文をよく読んで解いてください．