
今回は力学の問題です.
冷静に考えれば,確実に得点できると思います.
解答は最後にあります.
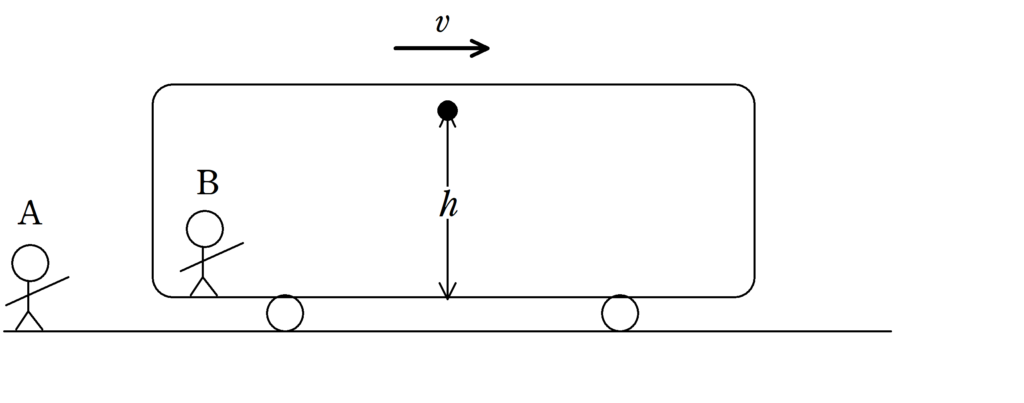
図のように,電車が速さ$v$で水平右向きに等速直線運動をしている.電車の外には静止した観測者Aが,電車の中には,電車に対して静止した観測者Bがいる.
電車内の底面より高さ$h$に大きさの無視できるボールが固定されている.時刻0でボールの固定をはずすと,Bからみて初速度0でボールは運動をはじめた.重力加速度の大きさを$g$として次の問いに答えよ.
(1) ボールがはじめに電車の底面に達する時刻$t_{0}$として正しいものを選べ.
$① t_{0}=\dfrac{h}{g}$ $② t_{0}=\sqrt{\dfrac{h}{g}}$ $③ t_{0}=\sqrt{\dfrac{2h}{g}}$ $④ t_{0}=\sqrt{\dfrac{h}{2g}}$ $⑤ t_{0}=\dfrac{-v+\sqrt{v^{2}+2gh}}{g}$
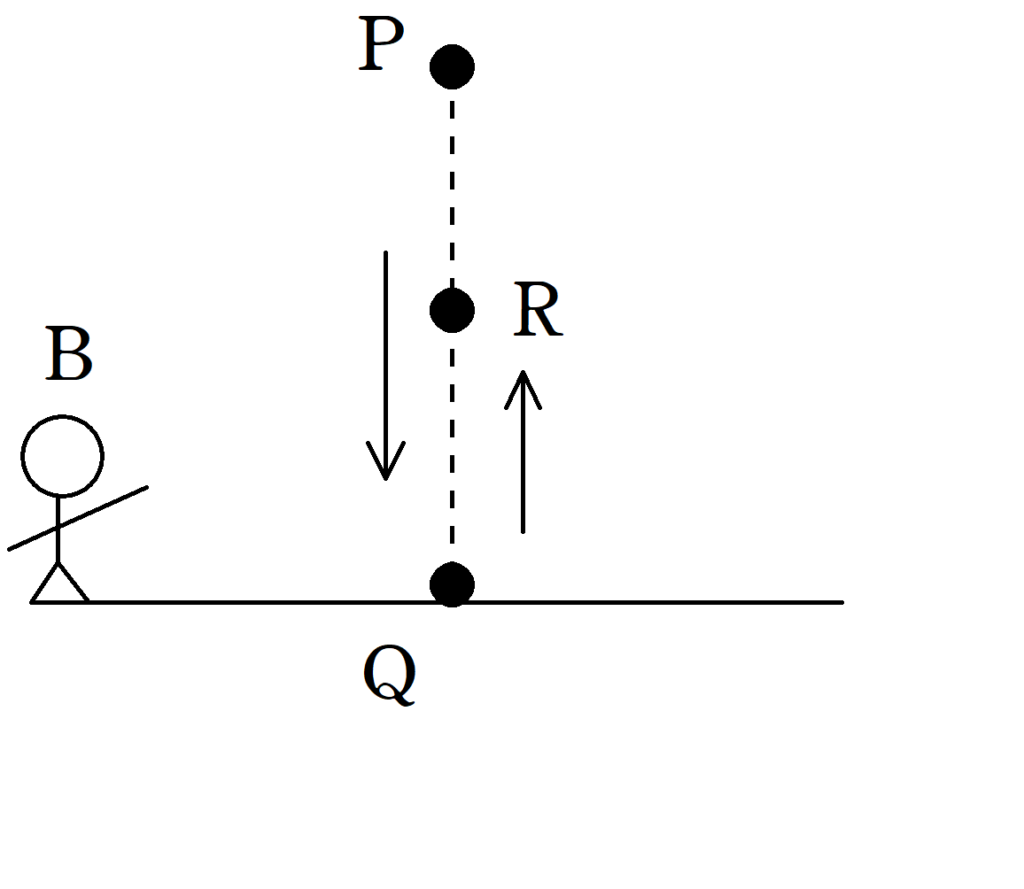
(2) $t=0$よりボールの運動をBからみると,ボールはP点より運動をはじめ,Q点で面に対して垂直に衝突して跳ね返り,R点で最高点に達した.衝突の前後で電車の速度の変化はないものとすると,観測者Aからみたボールの軌道はどのようになるか,①~⑥の中から最も適当なものを選びなさい.

<解答>
(1)

電車は等速度運動しているので,観測者Bからみたボールにはたらく力は重力だけだね!
つまり,ボールは等加速度運動するわけだね!
まずは,等加速度運動の式を確認しておきましょう.
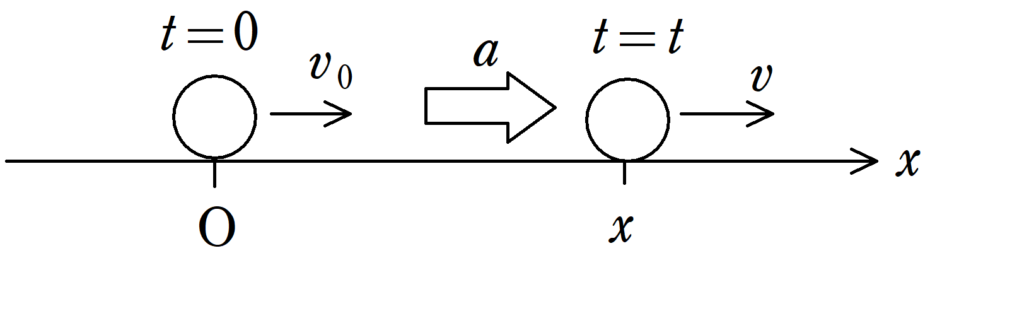
物体は加速度$a$で$x$軸上を運動している.$t=0$において,原点にある物体が,時刻$t$に座標$x$に移動した.初速度を$v_{0}$,時刻$t$における速度を$v$とするとき,次の関係式が成り立つ.
$v=v_{0}+at$ $\dots (\ast)$
$x=v_{0}t+\dfrac{1}{2}at^2$ $\dots (2\ast)$
$v^{2}-v_{0}^{2}=2ax$ $\dots (3\ast)$

今回は高さ$h$が与えられていることと,時刻$t_{0}$を聞かれていることから$(2\ast)$の式を立てましょう.
$x=v_{0}t+\dfrac{1}{2}at^{2}$

ここで,初速度は$v_{0}$です!
今回の観測者はBであることと,そもそも鉛直方向の等加速度運動の式を立てているので,電車の水平方向の速度は関係ありません!
$x=h$,$v_{0}=0$,$a=g$,$t=t_{0}$として
$h=\dfrac{1}{2}gt_{0}^{2}$ $\therefore t_{0}=\sqrt{\dfrac{2h}{g}}$
したがって,答えは$③$です.
(2)

次はAからボールの運動をみます.
相対速度の計算が苦手な人は下記の記事を読むことをおすすめします.
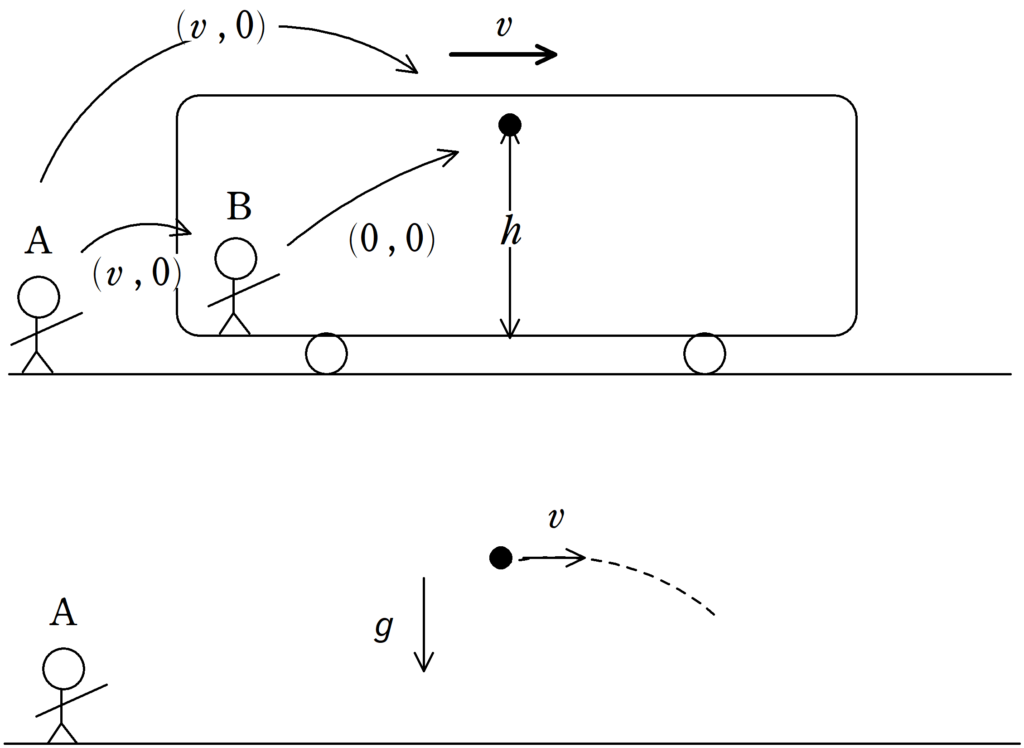

2次元運動なので速度を$(v_{x},v_{y})$の形で表します.$v_{x}$は右方向の速度,$v_{y}$は上方向の速度としましょう.
Bは電車とともに,右方向に速度$v$で動いていて,上下方向には動いていないので$(v , 0)$です.
また,$t=0$において,ボールはBからみて静止しているので$(0 , 0)$です.
ベクトルの足し算をするとAからみたボールの速度は
$(v , 0)+(0 , 0)=(v , 0)$
となります.ボールは重力しかはたらいていないので
水平右方向に初速をもっていて重力がはたらく→水平投射
となります.とりあえず,ボールが電車と衝突するまでは水平投射運動します.
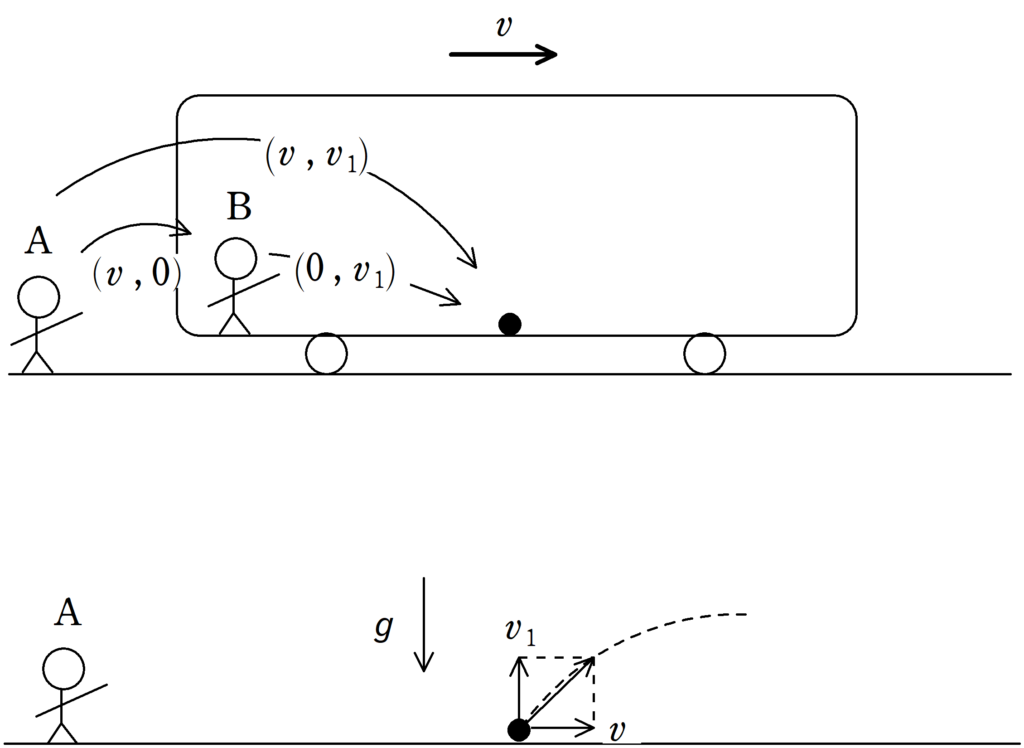

次にボールが電車と衝突した後について考えます.
衝突後Bからみた速度は$(0 , v_{1})$としましょう.
また,AからみたBの速度は同じく$(v , 0)$です.
したがって,ベクトルの足し算をすれば,Aからみたボールの速度は
$(v , 0)+(0 , v_{1})=(v , v_{1})$
つまり,ボールは上図のように,斜めに初速度をもって運動をします.やはり重力しかはたらかないので,ボールは放物運動をします.
したがって,答えは$①$となります.
以上より(1) $③$ (2) $①$




コメント