
断熱変化のときは圧力を$p$,体積を$V$,比熱比を$\gamma$とすると,
$pV^{\gamma}=$一定
が成り立つらしい.この式はどこから出てくるの??

ポアソンの式ですね.
この式は
- 理想気体の状態方程式
- 熱力学第一法則
から導くことができます.

気体の圧力を$p$,体積を$V$,絶対温度を$T$,物質量を$n$,気体定数を$R$とすると
$pV=nRT$
これを理想気体の状態方程式というんだね.

断熱的(熱の出入りを遮断して)に気体を変化させましょう.
すると,圧力,体積,絶対温度がそれぞれ,$p+\Delta p$,$V+\Delta V$,$T+\Delta T$になります.

すると,変化後の状態方程式は
$(p+\Delta p)(V+\Delta V)=nR(T+\Delta T)$
となるね.

そうです.
では,展開して整理してみましょう.
$\eqalign{(p+\Delta p)(V+\Delta V)&=nR(T+\Delta T)\cr pV+p\Delta V+V\Delta p +\Delta p \Delta V&=nRT+nR\Delta T\cr p\Delta V+V\Delta p+ \Delta p \Delta V&=nR\Delta T \dots (\ast) }$

上の途中で$pV=nRT$を使って整理しているね.

はい.
さらに,$\Delta p$や$\Delta V$を非常に小さい値としましょう.
すると,$(\ast)$は次の式のようになります.
$\Delta p \Delta V\fallingdotseq 0$より
$p\Delta V+V\Delta p=nR\Delta T$ $\dots (2\ast)$

また,体積が$\Delta V$変化したときの気体がした仕事$W$は
$W=p\Delta V$
です.

え?!圧力は変化しないの??さっきは圧力の変化も考えたのに...

気体がした仕事は$pV$図の面積でしたね.
こちらを参考にしてください.
$pV$図の面積は下図の青色部分となります.
断熱変化の際にどのような$pV$図になるかはまだわかりませんが,とりあえず一般的な曲線で考えていきます.
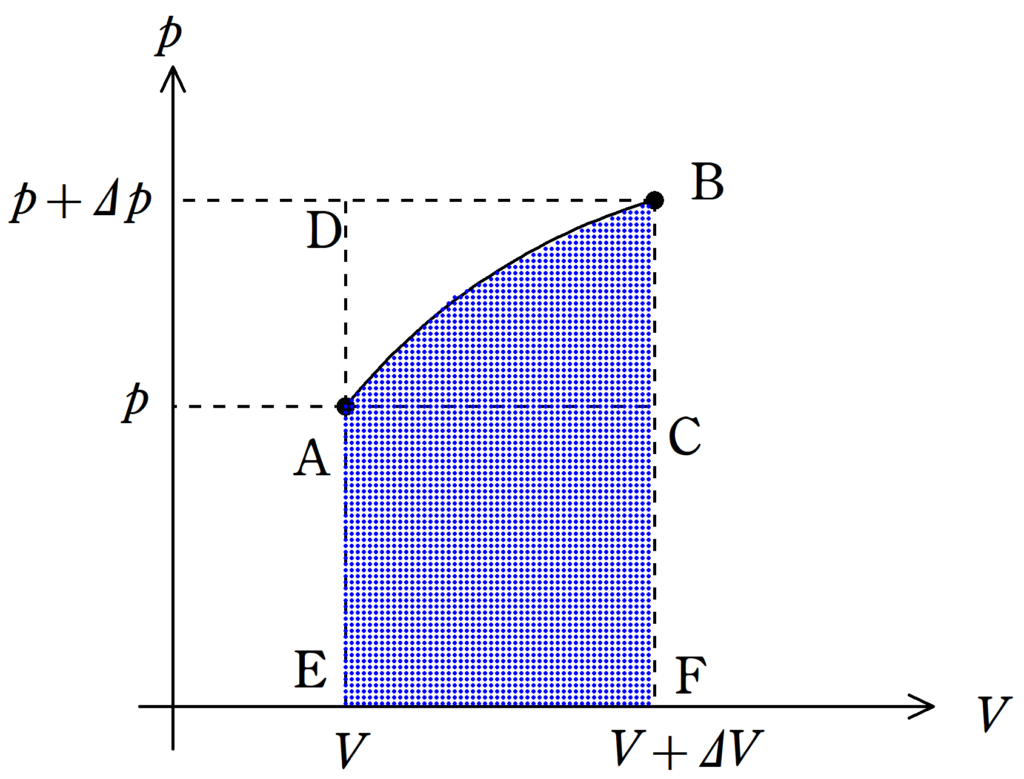

すると,この青色部分の面積は長方形AEFCより大きく,長方形よりDEFBより小さいことが確認できます.
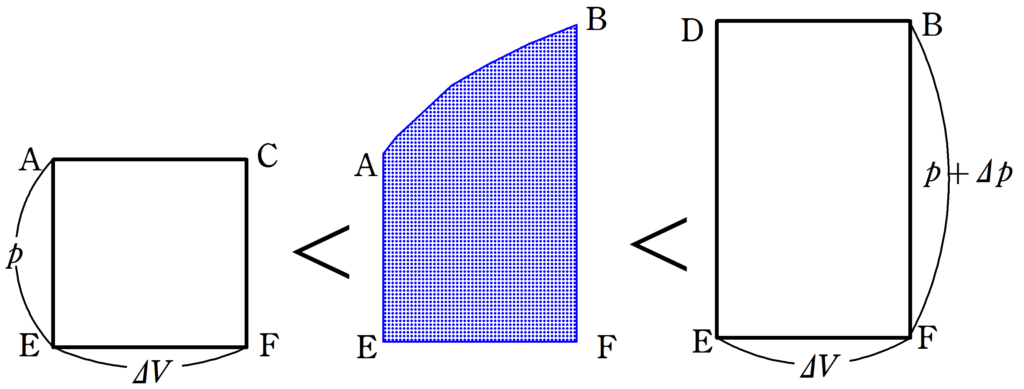
$p\Delta V<$青色部分の面積$<(p+\Delta p)\Delta V=p\Delta V+\Delta p \Delta V$ $\dots (\clubsuit)$
ここで,$\Delta V$を小さくしていくと,それにともない$\Delta p$も小さくなります.すなわち
$\Delta p \Delta V\fallingdotseq 0$
これを$(\clubsuit)$に代入すると,左辺も右辺も$p\Delta V$になるので,青色部分の面積は$p\Delta V$となります.
気体が微小体積$\Delta V$変化するとき,気体がする仕事$W$は圧力$p$を用いて
$W\fallingdotseq p\Delta V$
と近似できる.

気体がする仕事が$W=p\Delta V$であることが確認できたので,次にいきましょう.
熱力学第一法則は,内部エネルギーの変化を$\Delta U$,熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$ $\dots (3\ast)$
でした.
今回は断熱変化なので,$Q=0$です.さらに,定積モル比熱を$C_{\rm{V}}$とすれば,$\Delta U=nC_{\rm{V}}\Delta T$であることから$(3\ast)$は
$0=nC_{\rm{V}}\Delta T +p\Delta V$
$\Delta T=-\dfrac{p\Delta V}{nC_{\rm{V}}}$ $\dots (4\ast)$
となります.
$(4\ast)$を$(2\ast)$に代入しましょう.
$p\Delta V+V\Delta p=nR\Delta T$ $\dots (2\ast)$より
$\eqalign{p\Delta V+V\Delta p &=nR\cdot (-\dfrac{p\Delta V}{nC_{\rm{V}}})\cr p\Delta V+\dfrac{\cancel{n}R}{\cancel{n}C_{\rm{V}}}p\Delta V &=-V\Delta p\cr p\Delta V(1+\dfrac{R}{C_{\rm{V}}})&=-V\Delta p\cr p\Delta V\cdot (\dfrac{C_{\rm{V}}+R}{C_{\rm{V}}})&=-V\Delta p}$
ここで,理想気体のマイヤーの関係$C_{\rm{p}}=C_{\rm{V}}+R$と$\gamma=\dfrac{C_{\rm{p}}}{C_{\rm{V}}}$を使って,$\dfrac{C_{\rm{V}}+R}{C_{\rm{V}}}=\gamma$より
$p\Delta V \cdot \gamma =-V\Delta p $
両辺$pV$で割ると
$\eqalign{\gamma \dfrac{\Delta V}{V}&=-\dfrac{\Delta p}{p}\cr \dfrac{\Delta p}{p}&=-\gamma \dfrac{\Delta V}{V}}$
ここで,$\Delta p $,$\Delta V$は非常に小さいので,$\Delta p→dp$,$\Delta V→dV$として両辺積分をします.
積分するというのは何を意味しているのかを考えてみましょう.
$f(p)=-\dfrac{1}{p}$とおきましょう.すると,$f(p)\Delta p=\dfrac{\Delta p}{p}$は$f(p)-p$グラフの長方形の面積を表します.したがって,
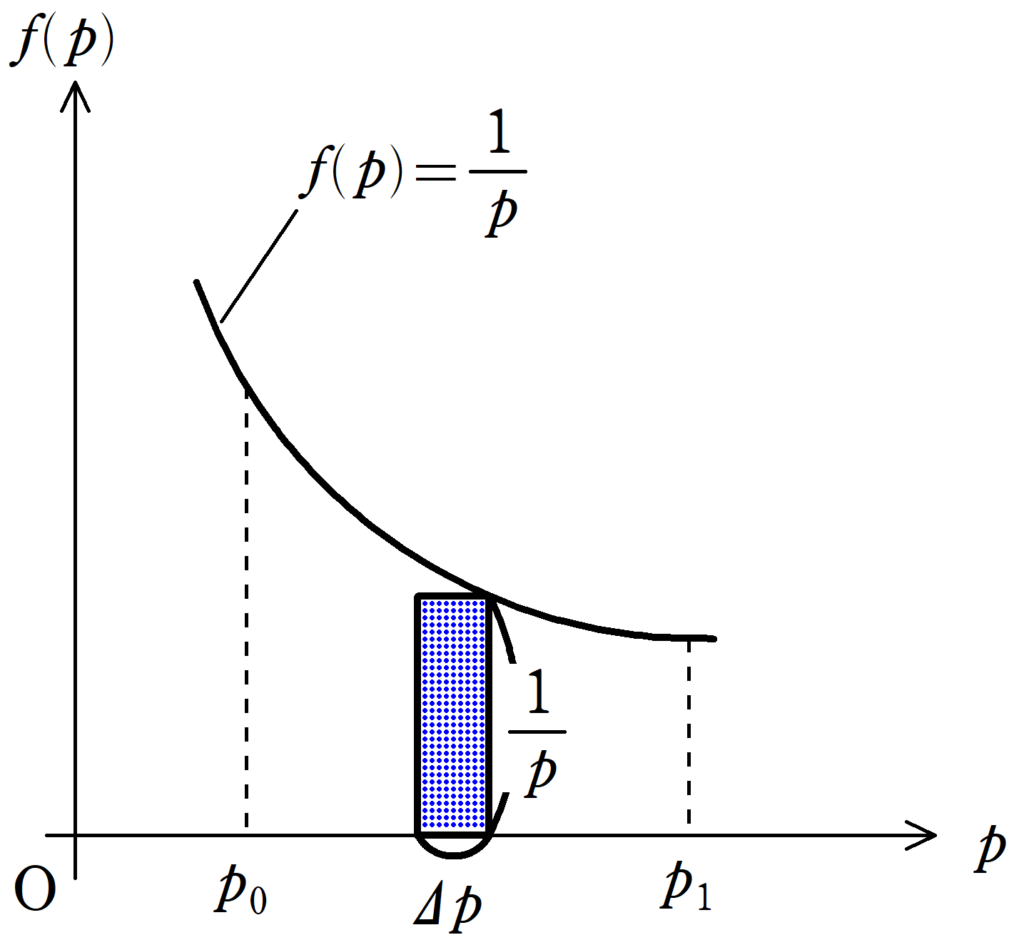
$\displaystyle{\int_{p_{0}}^{p_{1}} f(p)\,dp\fallingdotseq}$長方形の面積の和
となります.つまり,積分するということは,少しずつ変化する$\dfrac{\Delta p}{p}$を足し合わせるということを意味します.
$\dfrac{\Delta p}{p}=-\gamma \dfrac{\Delta V}{V}$の形では見えなかったことが積分する(足し合わせる)ことで使いやすい形にできないかと期待して変形をすることにしましょう.
さて,両辺積分をして,
$\displaystyle{\int \dfrac{1}{p}\,dp=-\gamma\int \dfrac{1}{V}\,dV }$
$\displaystyle{\int \dfrac{1}{x}\,dx=\log|x|+}$積分定数 を使いましょう.$\log$の底は自然対数$e$です.
$\eqalign{\log p &=-\gamma \log V +K\cr \log p+\log V^{\gamma}&=K \cr \log pV^{\gamma}&=K}$
$K$は積分定数です.したがって,
$pV^{\gamma}=$一定
が出てきます.
また,理想気体の状態方程式$pV=nRT$を$p=\dfrac{nRT}{V}$として上式に代入すれば,
$\dfrac{nRT}{V}V^{\gamma}$
$nR=$一定とすれば
$TV^{\gamma -1}=$一定
を得ます.

これらの式は,断熱変化であったらいつでも使えるというわけではありません.
ポアソンの式を導く過程で,微小量の和をとりました.
これはゆっくりと変化することを仮定しているので,準静的変化のときのみポアソンの式が成り立ちます.
準静的断熱変化をするとき,理想気体の圧力を$p$,体積を$V$,絶対温度を$T$,比熱比を$\gamma$とする.
ただし,$\gamma$は定積モル比熱$C_{\rm{V}}$と定圧モル比熱$C_{\rm{p}}$を用いて,$\gamma=\dfrac{C_{\rm{p}}}{C_{\rm{V}}}$.
このとき,以下のポアソンの式が成り立つ.
$pV^{\gamma}=$一定 ,$TV^{\gamma -1}=$一定

ちなみに,単原子分子理想気体では,定積モル比熱が$C_{\rm{V}}=\dfrac{3}{2}R$,定圧モル比熱が$C_{\rm{p}}=C_{\rm{V}}+R=\dfrac{5}{2}R$なので,比熱比は
$\gamma=\dfrac{C_{\rm{p}}}{C_{\rm{V}}}=\dfrac{\dfrac{5}{2}R}{\dfrac{3}{2}R}=\dfrac{5}{3}$
となるよ.したがって,ポアソンの式は
$\displaystyle{pV^{\frac{5}{3}}}=$一定
となるんだ.




コメント
[…] […]
[…] […]
[…] 準静的断熱変化の際に成り立つ式[ポアソンの式] […]
[…] (1)で圧力(や温度)を一定としたのにもかかわらず,(2)で圧力(や温度)が変化している理由ははやいうちに理解しておいた方がよい.(こちらでも紹介しています.) […]