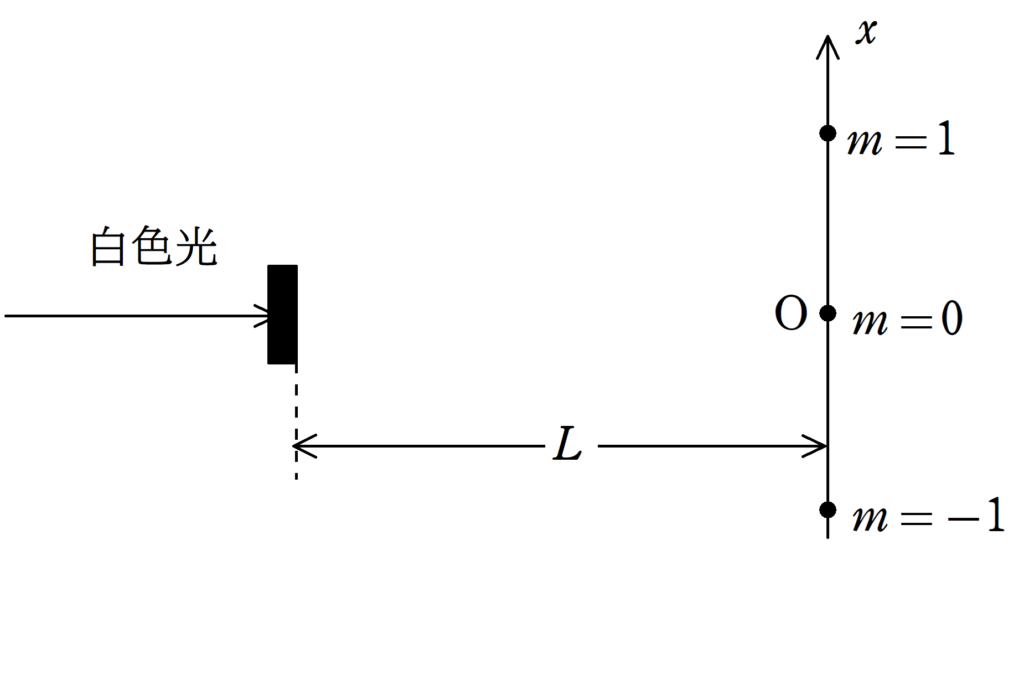
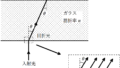
上図のように,格子定数$d$の回折格子に白色光を当てると,回折格子より距離$L$離れたスクリーンに3本の明線が観測された.
このうち,回折格子に真正面にある明線は白色で,その両隣りの明線は様々な色に分かれていた.
真正面の明線を$m=0$の明線とし,その両隣りの明線を$m=1$,$m=-1$とする.
$m=0$を原点とし,$m=1$に向かって$x$軸をとる.$m=1$の明線のうち,赤色の明線の座標を$x_{\rm R}$,紫色の明線の座標を$x_{\rm P}$とする.
赤色の波長を$\lambda_{\rm R}$,紫色の波長を$\lambda_{\rm P}$とするとき,$x_{\rm R}-x_{\rm P}$を$d$,$L$,$\lambda_{\rm R}$,$\lambda_{\rm P}$を用いて表せ.
ただし,$L$は$d$に比べて十分小さいものとする.
<解答>
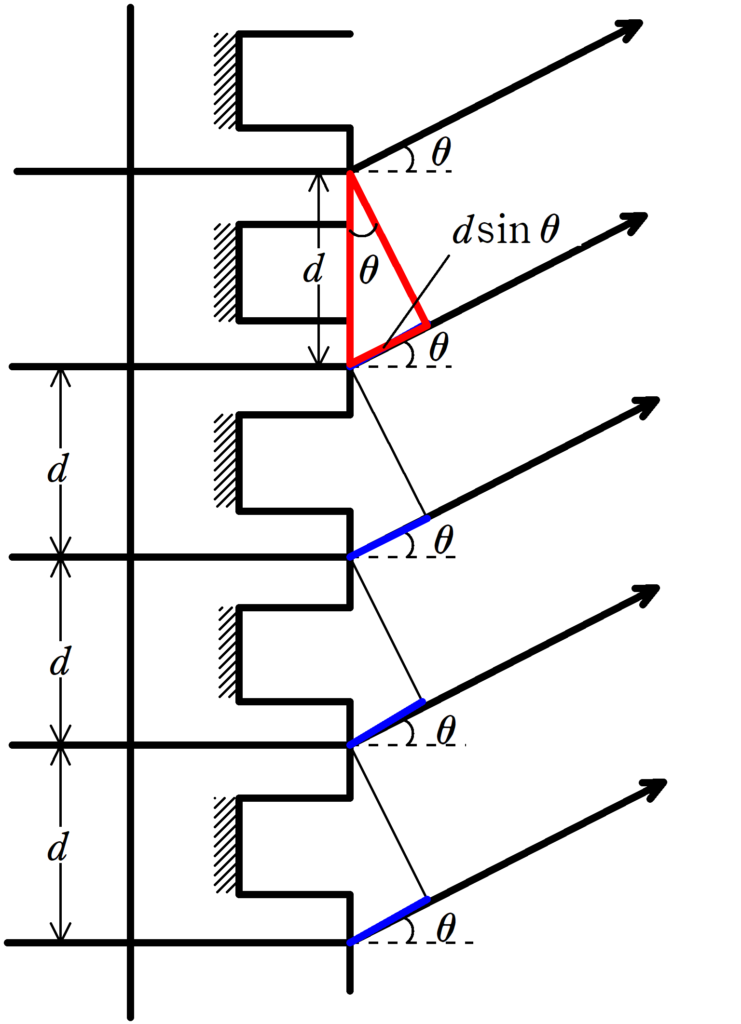

回折格子における強め合いの条件は,上の記事でも解いたように,波長を$\lambda$,格子定数を$d$,整数を$m$とし,光を当てた方向から$\theta$の角度における明線条件は
$\dfrac{d\sin\theta}{\lambda}=m$
$\therefore \sin\theta=\dfrac{m\lambda}{d}$ $\dots (\ast)$
となります.
今回は,回折格子とスクリーンまでの距離$L$が与えられているので,ヤングの実験と同様の近似を行います.
上の記事の経路差の求め方②で説明しています.
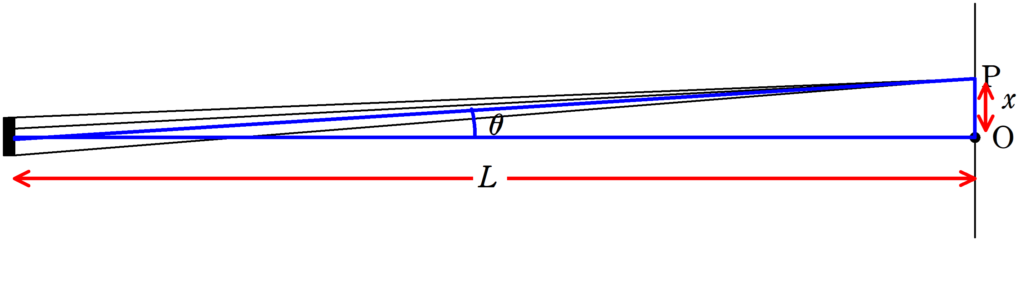

ここで,$|\theta|$が小さいときに使える近似式
$\sin\theta \approx \tan\theta$
を用いて
上の図の直角三角形について
$\tan\theta=\dfrac{x}{L}$
$\tan\theta\approx\sin\theta$より
$\sin\theta\approx\dfrac{x}{L}$
これを$(\ast)$の$\sin\theta=\dfrac{m\lambda}{d}$に代入しましょう.
$\dfrac{x}{L}=\dfrac{m\lambda}{d}$
$\therefore$ $x=\dfrac{mL\lambda}{d}$ $\dots (\spadesuit)$

さて,問題にうつりましょう.
$(\spadesuit)$について,$m=1$を代入すると
$x=\dfrac{L\lambda}{d}$
となり,明線の座標は波長によって決まることがわかります.
$m=1$の明線のうち,赤色の座標$x_{\rm R}$と紫色の座標$x_{\rm P}$は次のようになります.
$x_{\rm R}=\dfrac{L\lambda_{\rm R}}{d}$
$x_{\rm P}=\dfrac{L\lambda_{\rm P}}{d}$
差をとって
$\eqalign{x_{\rm R}-x_{\rm P}&=\dfrac{L\lambda_{\rm R}}{d}-\dfrac{L\lambda_{\rm P}}{d}\\&=\dfrac{L}{d}(\lambda_{\rm R}-\lambda_{\rm P})}$
ということで,答えは$x_{\rm R}-x_{\rm P}=\dfrac{L}{d}(\lambda_{\rm R}-\lambda_{\rm P})$




コメント