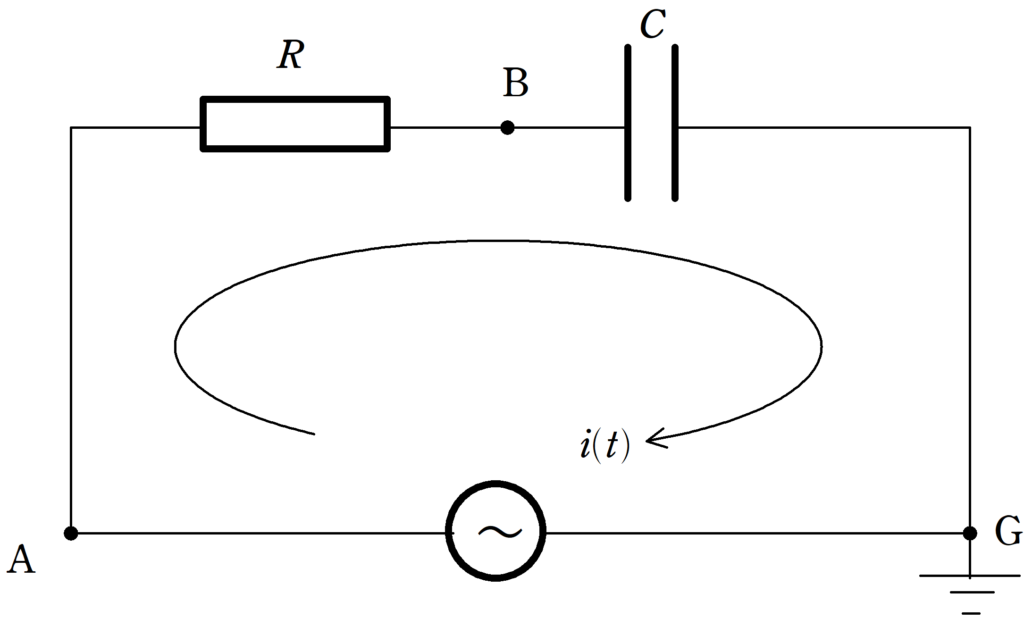
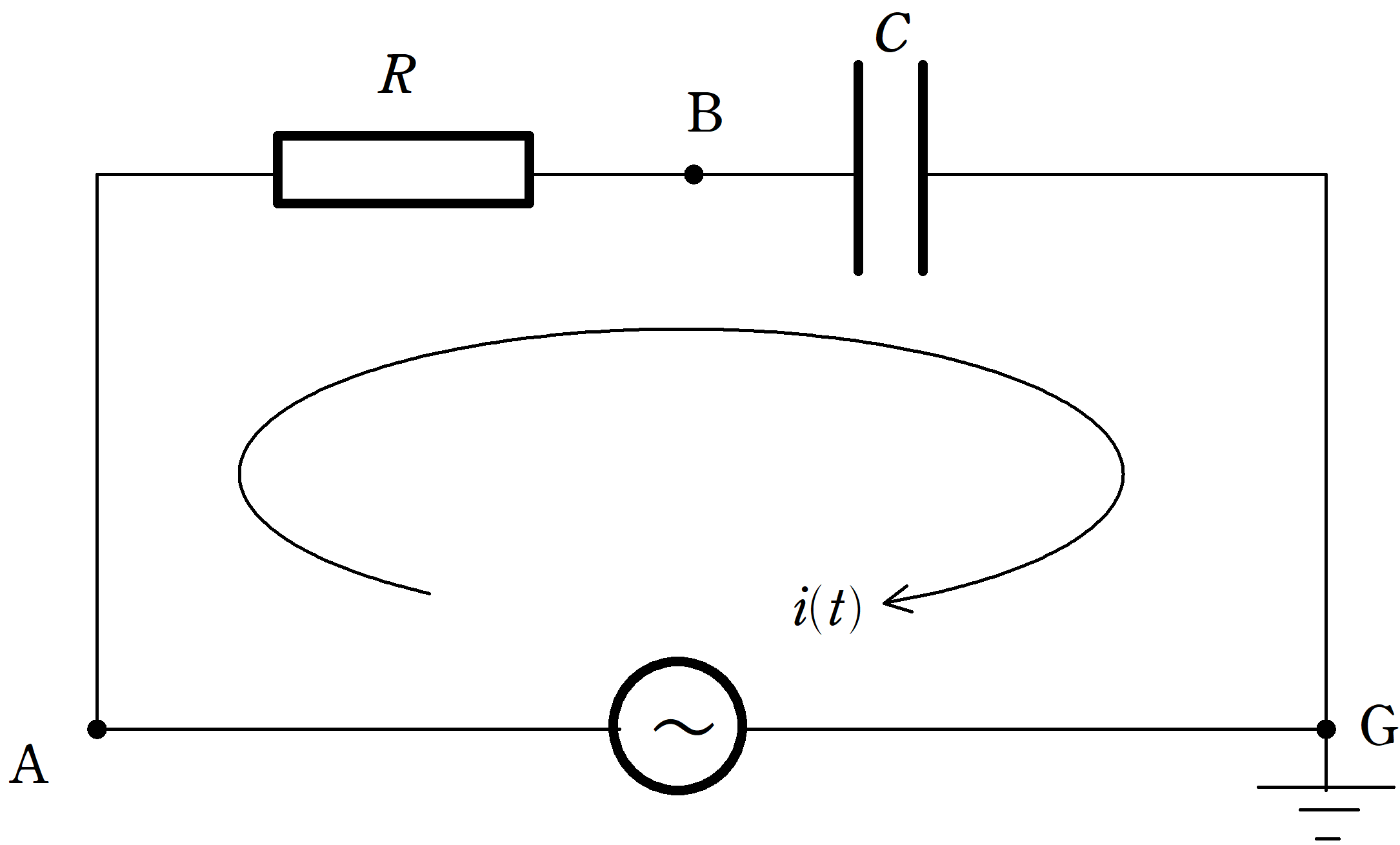
上図のように抵抗値$R$の抵抗と,電気容量$C$のコンデンサーを直列につなげ,交流電源に接続した.図の向きに$i(t)=i_{0}\sin\omega t$の電流が流れているとき,次の問いに答えよ.
ただし,$i_{0}>0$であり,$\omega$は角周波数である.
(1) Bに対するAの電位$V_{\rm R}$を求めよ.
(2) Gに対するBの電位$V_{\rm C}$を求めよ.
(3) Gに対するAの電位$V(t)$を求めよ.
(4) この回路のインピーダンス$Z$を求めよ.
(5) この回路の平均消費電力$\bar{P}$を求めよ.
<解答>

交流の問題は次のことを確認しておきましょう.
● 最大値について
回路素子にかかる電圧の最大値を$V_{0}$,流れる電流の最大値を$I_{0}$,リアクタンス(または抵抗)を$Z$とする.
このとき,次の関係が成り立つ.
$V_{0}=ZI_{0}$
$Z$は回路素子できまる.各周波数を$\omega$として
抵抗値$R$の抵抗のとき,$Z=R$
電気容量$C$のコンデンサーのとき,$Z=\dfrac{1}{\omega C}$
自己インダクタンス$L$のコイルのとき,$Z=\omega L$
● 位相のずれについて
1)電圧に対する電流の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$進む(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$遅れる(電圧が先に変化し,遅れて電流が変化する)
2)電流に対するで電圧の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$遅れる(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$進む(電圧が先に変化し,遅れて電流が変化する)
(1)

抵抗に電流$i(t)$が流れていることがわかっています.
このとき,抵抗にかかる電圧の位相は電流の位相と同じです.
また,電圧の最大値$V_{\rm R0}$は
$V_{\rm R0}=Ri_{0}$
から求めることができます.
$\eqalign{V_{R}&=V_{\rm R0}\sin\omega t\\&=Ri_{0}\sin\omega t}$ (答)
(2)

コンデンサーの電圧は電流に対して$\dfrac{\pi}{2}$遅れます.
コンデンサーの式$Q=CV$は瞬間々々成り立ちます.
つまり,$Q$と$V$の位相は同じです.
一方,交流回路において,電流は電荷より先に変化します.
電流が流れてから電荷が変化するのです.
また,電圧の最大値$V_{\rm C0}$は
$V_{\rm C0}=\dfrac{1}{\omega C}i_{0}$
を満たします.
$\eqalign{V_{C}&=V_{\rm C0}\sin(\omega t-\dfrac{\pi}{2})\\&=-\dfrac{i_{0}}{\omega C}\cos \omega t}$ (答)
(3)

キルヒホッフ則より
$V(t)=V_{\rm R}+V_{\rm C}$
が成り立ちます.
$\eqalign{V(t)&=Ri_{0}\sin\omega t-\dfrac{i_{0}}{\omega C}\cos\omega t\\&=i_{0}\sqrt{R^{2}+(\dfrac{1}{\omega C})^{2}}\sin(\omega t +\phi)}$ (答)
ただし,$\tan\phi =-\dfrac{\dfrac{1}{\omega C}}{R}=-\dfrac{1}{R\omega C}$

上の式変形では,三角関数の合成を用いました.
(4)

(3)より,交流電源の電圧の最大値$V_{0}$は
$V_{0}=i_{0}\sqrt{R^{2}+(\dfrac{1}{\omega C})^{2}}$
となります.
回路全体にかかる電圧の最大値を$V_{0}$,電流の最大値を$I_{0}$とするとき,インピータンス$Z$は次のように決める.
$Z=\dfrac{V_{0}}{I_{0}}$
インピーダンス$Z$は
$Z=\dfrac{V_{0}}{i_{0}}=\sqrt{R^{2}+(\dfrac{1}{\omega C})^{2}}$ (答)
(5)

回路の消費電力$P(t)$は
$P(t)=V(t)i(t)$
です.
平均消費電力を求めやすくするように,
$V(t)=Ri_{0}\sin\omega t-\dfrac{i_{0}}{\omega C}\cos\omega t$
を採用しましょう.
$\eqalign{P(t)&=V(t)i(t)\\&=(Ri_{0}\sin\omega t-\dfrac{i_{0}}{\omega C}\cos\omega t)\cdot i_{0}\sin\omega t\\&=Ri_{0}^{2}\sin^{2}\omega t -\dfrac{i_{0}^{2}}{\omega C}\sin\omega t \cos\omega t}$

ここで,$\sin\omega t\cos\omega t=\dfrac{1}{2}\sin 2\omega t$
(倍角の式)の時間平均は0,$\sin^{2}\omega t$の時間平均は$\dfrac{1}{2}$となります.
$\bar{P}=\dfrac{i_{0}^{2}}{2R}$ (答)

コメント