[交流]　電力と静電エネルギーの関係[コンデンサー]

NEKO

今回は，電力と静電エネルギーの関係について話をしたいと思います．

この2つにはどのような関係があるのでしょうか？

NEKO

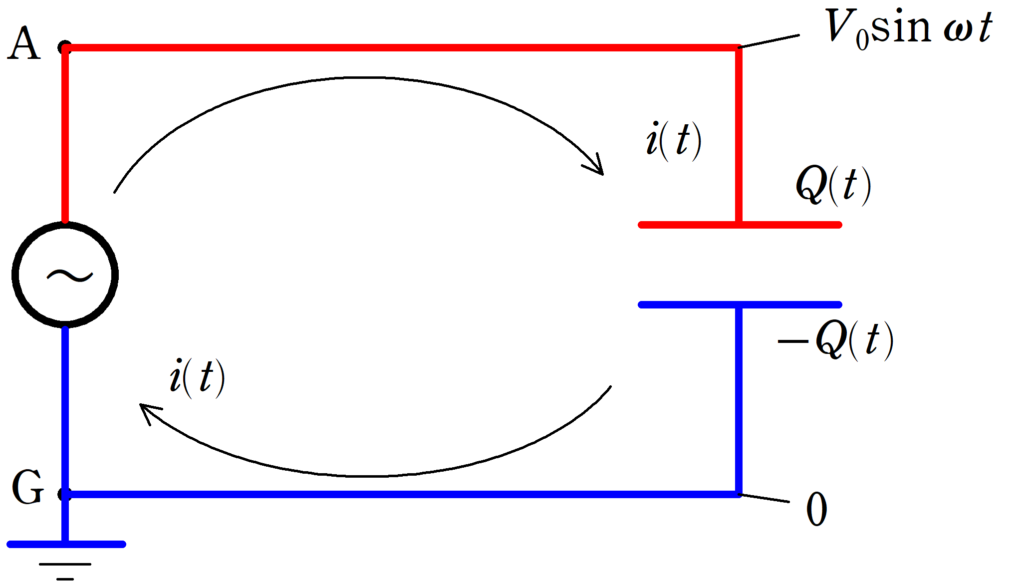
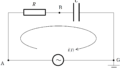
上図のように，時刻$t$において，Gに対するAの電位が$V(t)=V_{0}\sin\omega t$のとき，電流$i(t)$を求めましょう．

回路素子にかかる電圧または電流のどちらかがわかっているとき，電流または電圧を求めるときは，次のステップで解きましょう．

★　電流の最大値

電流の最大値を$i_{0}$とすると

$V_{0}=\dfrac{1}{\omega C}i_{0}$　$\therefore　i_{0}=\omega CV_{0}$

★　位相のずれ

コンデンサーに流れる電流は，電圧に対して位相が$\dfrac{\pi}{2}$進む．

以上から時刻$t$における電流$i(t)$は

$\eqalign{i(t)&=\omega CV_{0}\sin(\omega t+\dfrac{\pi}{2})\\&=\omega CV_{0}\cos\omega t}$

NEKO

電力を計算してみましょう．

電力$P$は電流を$I$，電圧を$V$とすると

$P=IV$

で表されます．

★　電力$P(t)$の計算

$\eqalign{P(t)&=i(t)V(t)\\&=(\omega CV_{0}\cos\omega t)\cdot (V_{0}\sin \omega t)\\&=\omega CV_{0}^{2}\sin\omega t \cos\omega t　\dots　(\ast)}$

NEKO

一方，コンデンサーに蓄えられるエネルギー$U$は次のようになります．

★　静電エネルギー$U$

$\eqalign{U&=\dfrac{1}{2}CV(t)^{2}\\&=\dfrac{1}{2}C(V_{0}\sin\omega t)^{2}\\&=\dfrac{1}{2}CV_{0}^{2}\sin^{2}\omega t　\dots　(2\ast)}$

NEKO

さて，$(\ast)$と$(2\ast)$はどのような関係があるのでしょうか？

電力$P$は

「単位時間当たりの電流がする仕事」

静電エネルギーは

「時刻$t$にコンデンサーに蓄えられているエネルギー」

です．

すると，単位時間当たりに電流が仕事をした分だけ，静電エネルギーが変化していることが予想できます．

では，確かめていきましょう．

静電エネルギー$U$を時間$t$で微分しましょう．

$\eqalign{\dfrac{dU}{dt}&=\dfrac{d}{dt}(\dfrac{1}{2}CV_{0}^{2}\sin^{2}\omega t)\\&=\dfrac{1}{2}CV_{0}^{2}\dfrac{d}{dt}(\sin^{2}\omega t)\\&=\dfrac{1}{2}CV_{0}^{2}\cdot (\sin\omega t)^{\prime}\cdot 2\sin\omega t\\&=\omega CV_{0}^{2}\sin\omega t \cos\omega t}$

NEKO

やはり，$(\ast)$の形と同じになりましたね．

電力$=$静電エネルギーの変化

が成り立っています．

交流電源につないだとき，静電エネルギーは増加と減少を周期的に繰り返し，その結果，電力の平均は0となります．

こちらの記事で具体的な計算をしているので参考にしてください．

交流演習　コンデンサーをつなぐ

問題 上図のように，交流電源と電気容量$C$のコンデンサーをつないだ． 時刻$t$におけるGに対するAの電位が$V(t)=V_{0}\sin\omega t$のとき，次の問いに答えよ． ただし，$V_{0}>0$とする． (1)　時刻$t$...

physicmath.net

2021.01.26