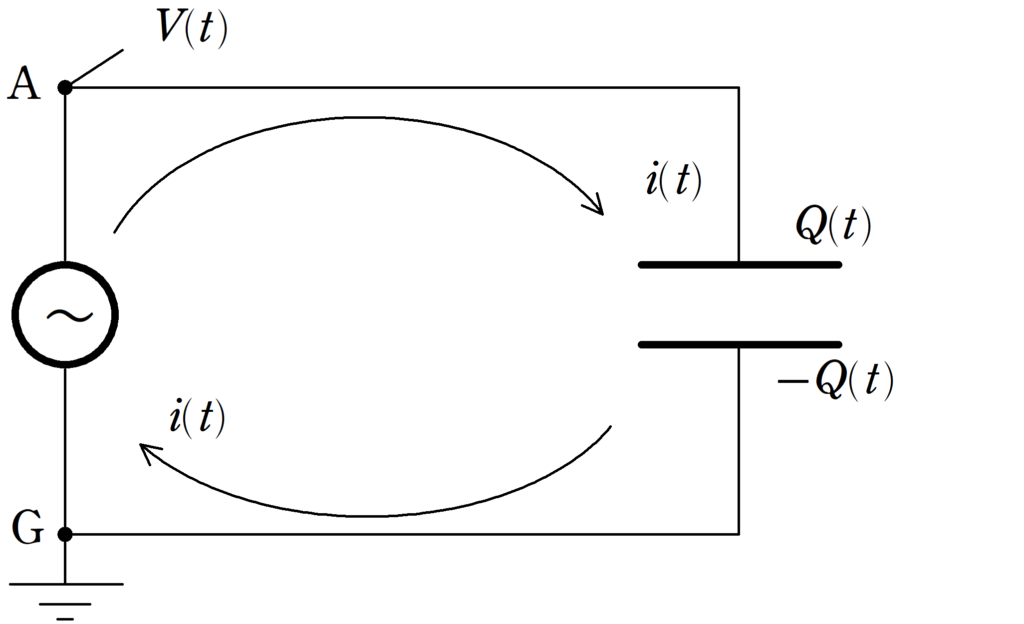
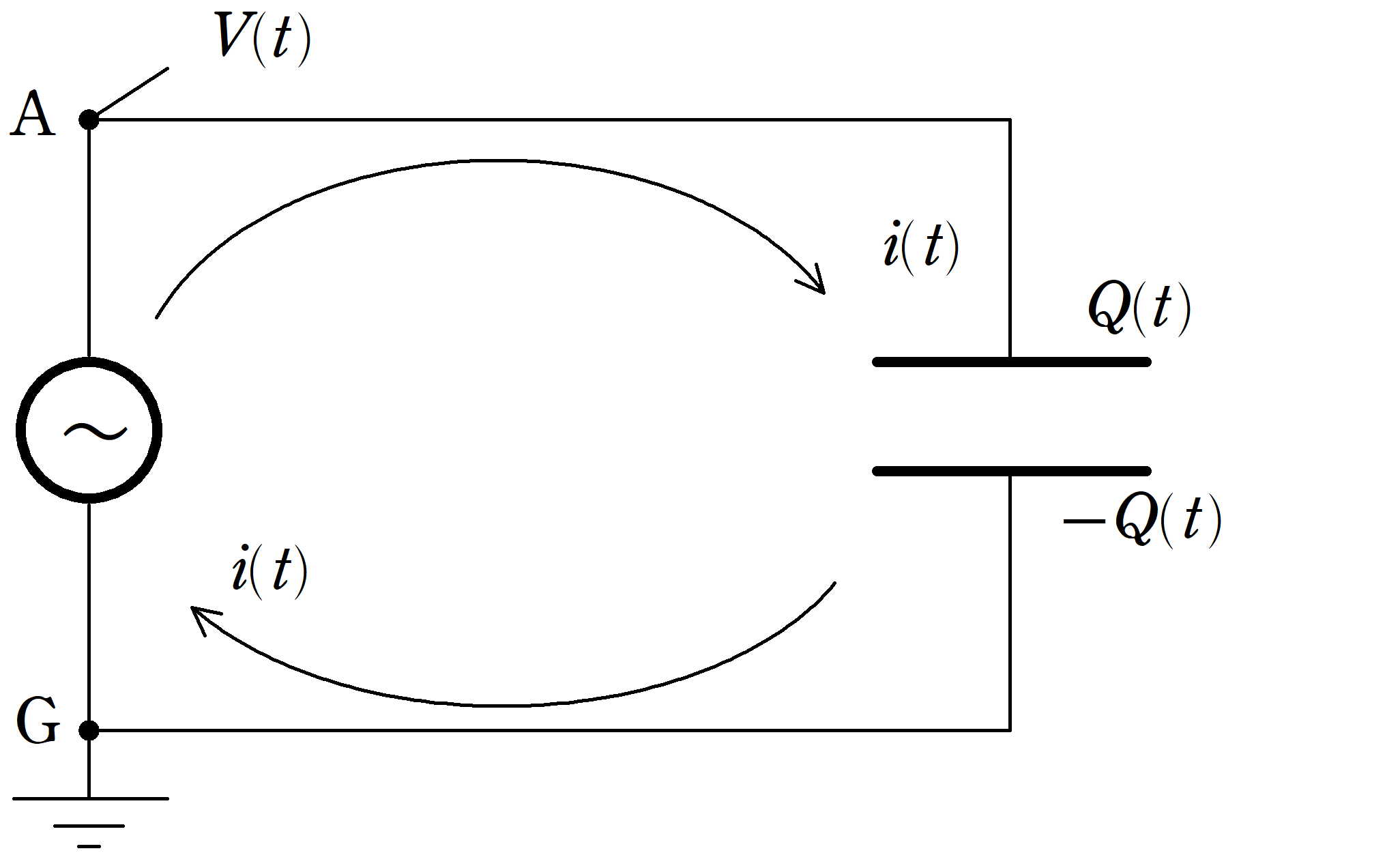
上図のように,交流電源と電気容量$C$のコンデンサーをつないだ.
時刻$t$におけるGに対するAの電位が$V(t)=V_{0}\sin\omega t$のとき,次の問いに答えよ.
ただし,$V_{0}>0$とする.
(1) 時刻$t$において,A側にある極板に蓄えられている電荷$Q(t)$を求めよ.
(2) 回路に流れる電流を上図の向きに$i(t)$とする.$i(t)$を求めよ.
(3) コンデンサーの平均電力$\bar P$を求めよ.
<解答>
(1)

コンデンサーの基本式が任意の時刻で成り立ちます.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
★ コンデンサーの基本式
$\eqalign{Q(t)&=CV(t)\\&=CV_{0}\sin\omega t}$ (答)
(2)

電流の定義式を使いましょう.
時間$\varDelta t$の間に電気量$\varDelta Q$が通過するときの電流の大きさ$i$は
$i=\dfrac{\varDelta Q}{\varDelta t}$
$Q$が時間$t$の一次関数以外のときは,$\varDelta t\rightarrow 0$として
$\displaystyle{i=\lim_{\varDelta t\rightarrow 0}\dfrac{\varDelta Q}{\varDelta t}=\dfrac{dQ}{dt}}$
★ 電流の定義式
$\eqalign{i(t)&=\dfrac{dQ(t)}{dt}\\&=CV_{0}\dfrac{d}{dt}(\sin\omega t)\\&=\omega CV_{0} \cos\omega t}$ (答)

上の式より,$i(t)$の最大値は$\omega CV_{0}$となります.電流の最大値を$i_{0}$とすれば
$i_{0}=\omega CV_{0}$
$\therefore V_{0}=\dfrac{1}{\omega C}i_{0}$
このとき,$\dfrac{1}{\omega C}$を容量リアクタンスといいます.
(3)

電力の時間変化は$P(t)$は
$P(t)=i(t)V(t)$
です.
★ 電力
$\eqalign{P(t)&=i(t)V(t)\\&=(\omega CV_{0}\cos\omega t)\cdot(V_{0}\sin\omega t)\\&=\omega CV_{0}^{2}\sin\omega t \cos\omega t}$

倍角の式使って,電力の式を変形しましょう.
$\sin\theta=2\sin\theta\cos\theta$
$P=\omega CV_{0}^{2}\cdot \dfrac{1}{2}\sin 2\omega t$

$\sin 2\omega t$の平均は$0$になります.
したがって,コンデンサーの平均電力は$0$です.

コメント
[…] 交流演習 コンデンサーをつなぐ問題上図のように,交流電源と電気容量$… 分野別 物理のよくある質問 電磁気 高校物理 シェアする Twitter Facebook はてブ LINE physicmathをフォローする physicmath Physicmath(フィジクマス) […]
[…] 交流演習 コンデンサーをつなぐ問題上図のように,交流電源と電気容量$… […]