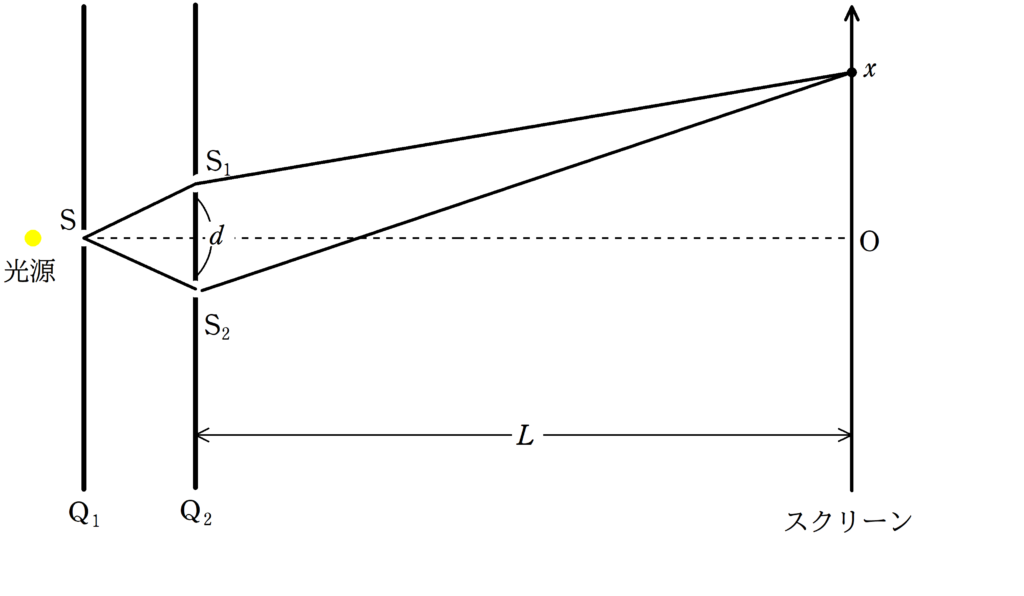
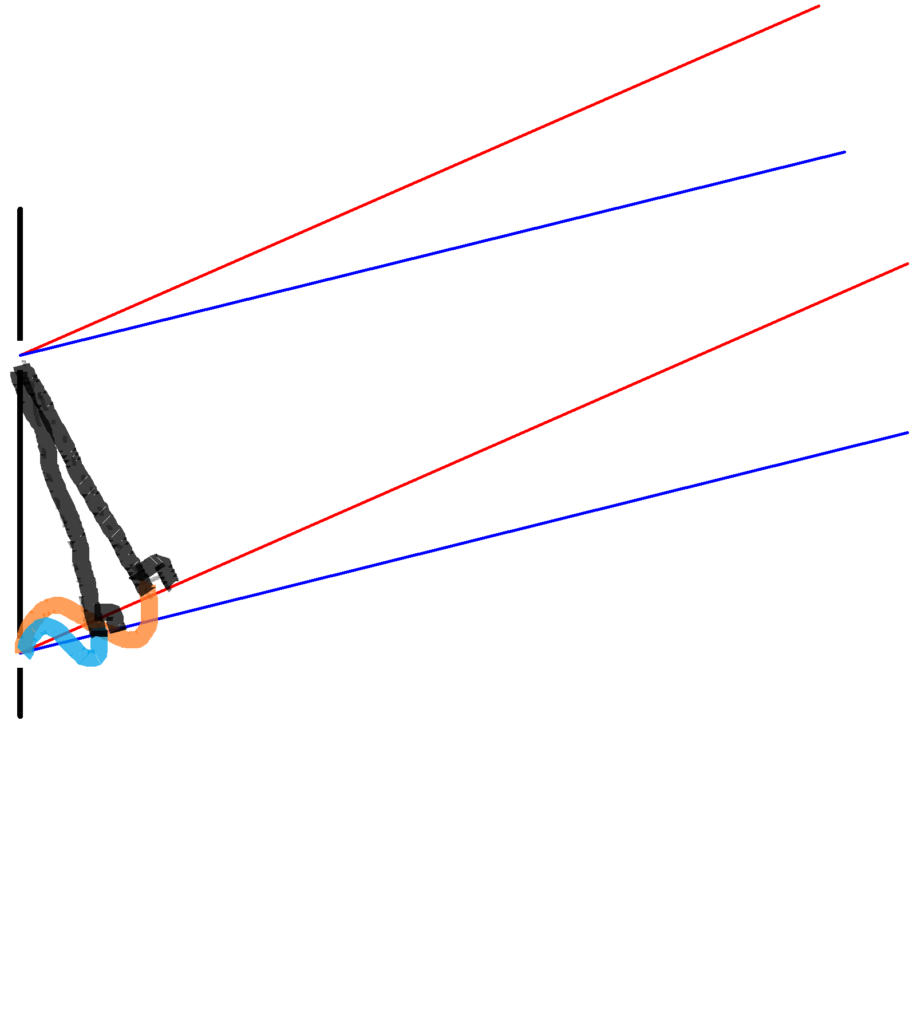
ついたて$\rm Q_{1}$,$\rm Q_{2}$,スクリーンが平行に設置されている.
$\rm Q_{2}$とスクリーンの距離は$L$である.
$\rm Q_{2}$には間隔$d$のスリットがあり,スリットの垂直二等分線と$\rm Q_{1}$との交点にスリット$\rm S$がある.
スリット$\rm S$の左側より,白色光の光を当てたところ,スクリーンに明暗の縞模様ができた.
2スリット$\rm S_{1}$,$\rm S_{2}$の垂直2等分線とスクリーンとの交点を原点$\rm O$としスクリーン上に$x$軸をとる.
このとき,原点に現れる色と,原点に一番近い色は何かを答えよ.
ただし,$d$は$L$に比べて十分小さいとする.

前回の内容はこちら.

さて,今日は,色ごとに波長が違うという話からしましょう.
何色が波長が大きくて,何色が波長が小さいのかを知っておくとよいでしょう.
覚え方は別記事で書きますので,確認にとどめておきましょう.
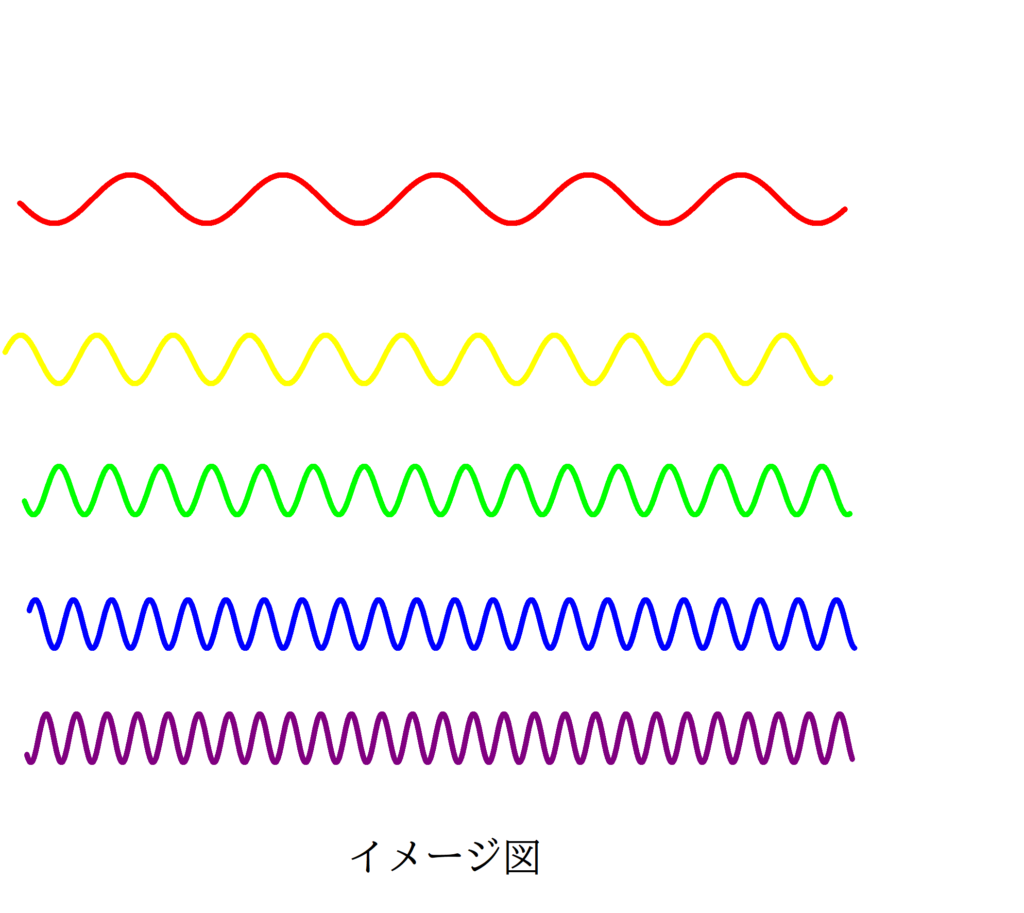

可視光線の中では,赤色が一番波長が大きいんだよね.穏やかで赤外線のようにエネルギーもあまり大きくないイメージがある.
そして,紫が一番波長が小さいんだよね.逆に紫外線のようにエネルギーが高いイメージ.

そうですね.
赤色は$7.0×10^{-7} \rm m$ほど,紫は$4.0×10^{-7} \rm m$ほどです.

じゃあ,前回と同様に,明線条件を考えてみよう.
★ 明線条件
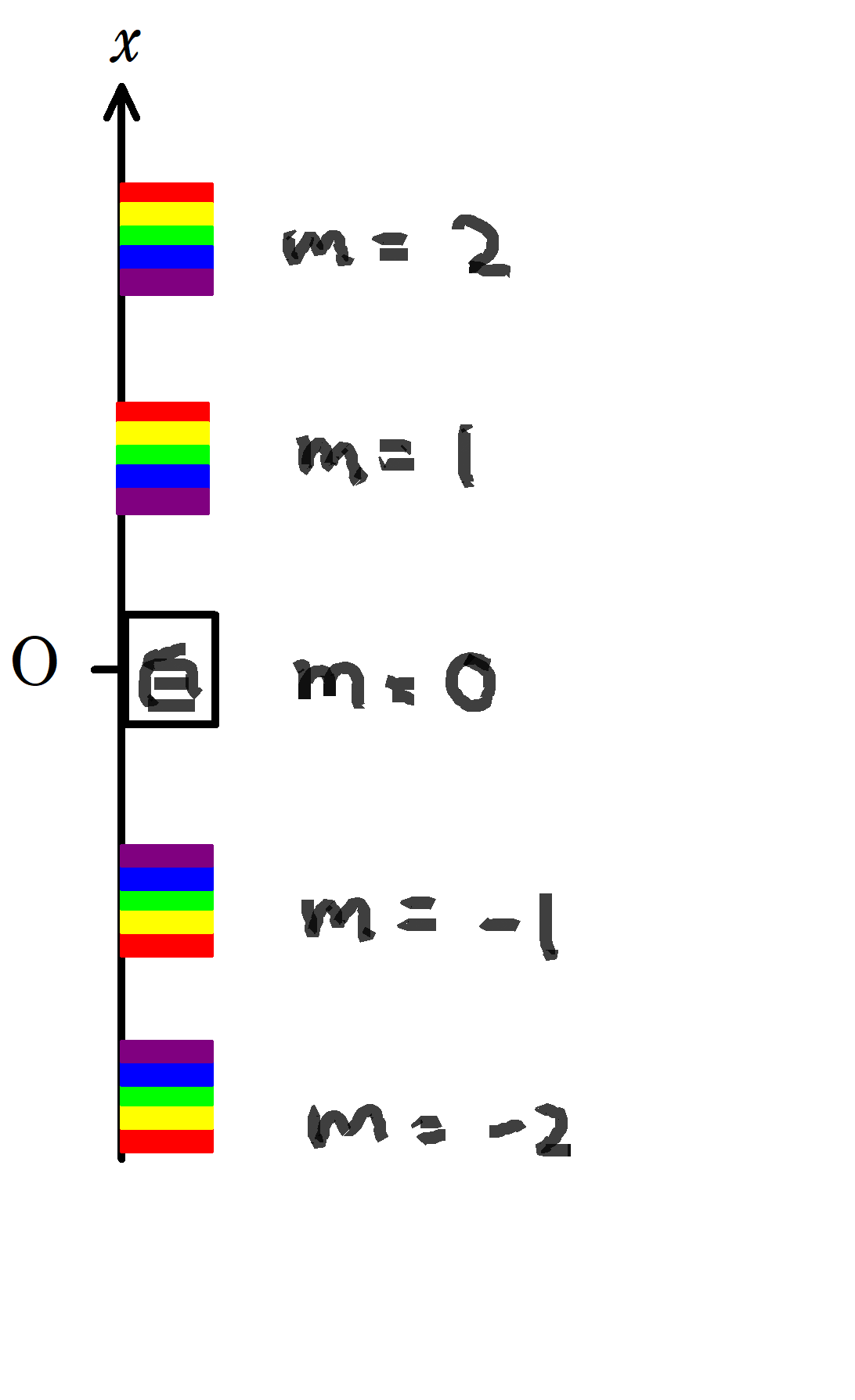
次数$m$の明線ができる座標を$x_{m}$としましょう.
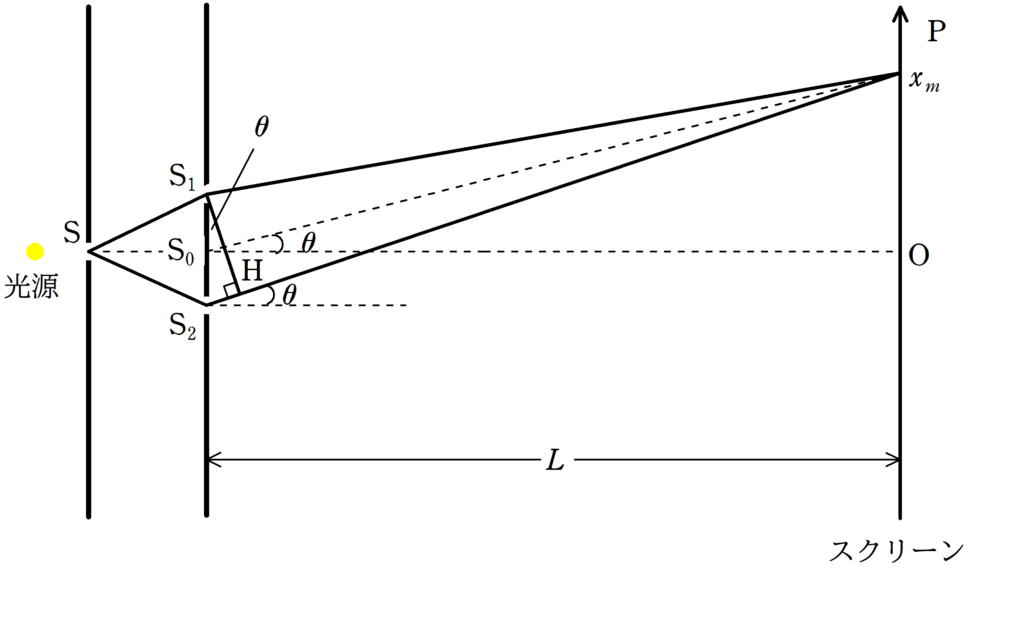
経路差は
$d\sin\theta\approx d\tan\theta \approx d\dfrac{x_{m}}{L}$
したがって,明線条件は
$\dfrac{d\dfrac{x_{m}}{L}}{\lambda}=m$
$\therefore x_{m}=\dfrac{mL\lambda}{d}$

$x_{m}=\dfrac{mL\lambda}{d}$の式をみると,$m$が決まっているとき,明線ができる座標は$\lambda$で決まるのがわかるね.
$\lambda$が小さいと$|x_{m}|$が小さくなるんだね.
ってことは,原点に近い方の色は波長が小さい紫になるね.
でも,原点はどうなるんだろう??

$m=0$なので,$\lambda$によらずにすべての色が原点に集まります.
すると,白色にみえます.

じゃあ,次のような色がスクリーンに現れるんだね.
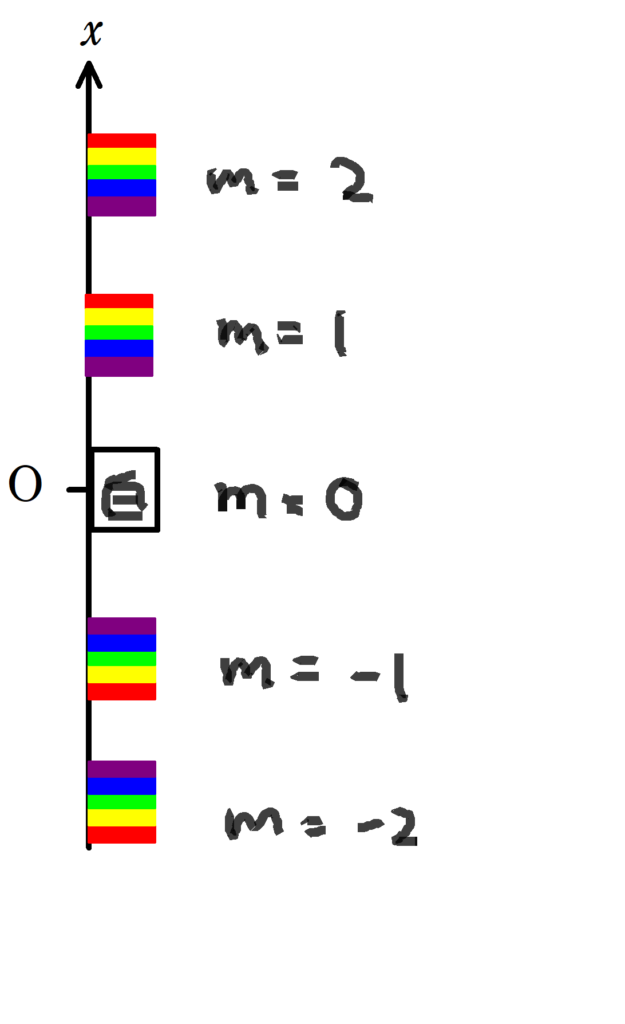

ということで,原点は白色で,原点から一番近い色は紫色でした.
ちなみに,数式ではなく,イメージでもとらえられるとよいですね.
赤色は波長が大きい分波1個分の差が出てくるのは紫より角度が急にならなくてはいけないんです.


コメント
[…] […]
[…] […]
二次光は全て虹色としてはっきり見えますか?
三次光の短波長達と、二次光の長波長達が重なる気がするのですが
メールにて送らせていただきました。