[標準]導体棒とコンデンサー② | Physicmath（フィジクマス）

PHYさん

引き続き導体棒とコンデンサーの問題です．

前回の内容はこちら

問題

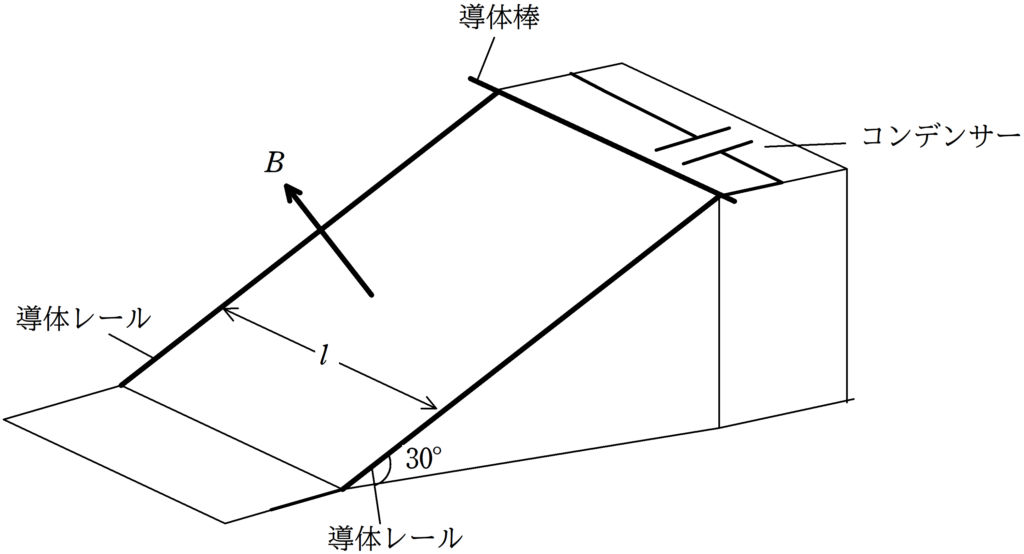
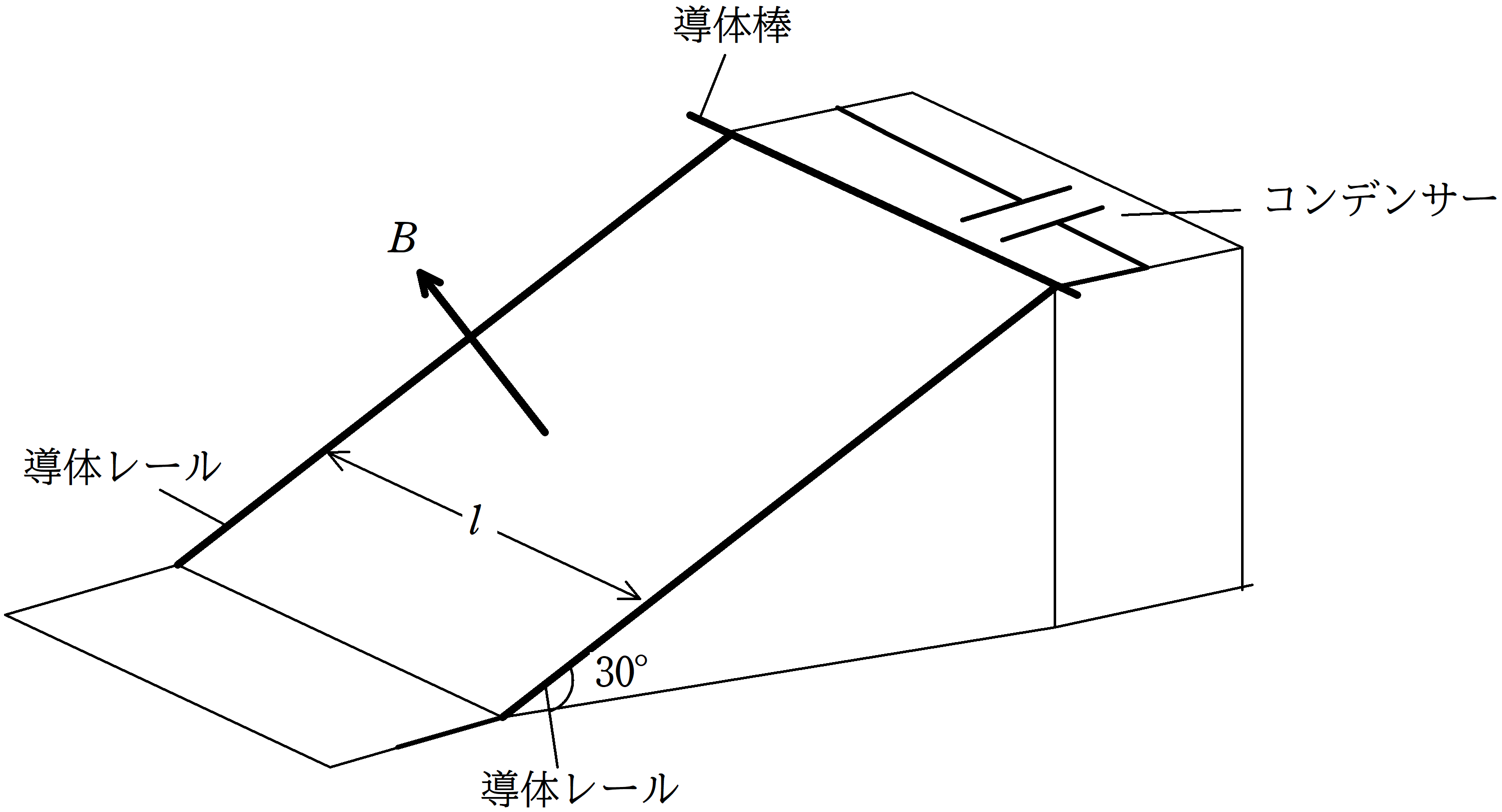
上図のように，傾角$30°$の斜面に間隔$l$で導体レールを平行に敷き，電荷が蓄えられていない電気容量$C$のコンデンサーを接続した．

斜面に対して垂直上向きに磁束密度の大きさ$B$の磁場をかける．

時刻$t=0$に質量$m$の導体棒を導体レールに垂直に交わるようにのせ，静かに手をはなすと，導体レールは運動をはじめた．

ただし，重力加速度の大きさを$g$として，導体棒は摩擦なく運動をする．

また，電気抵抗以外の抵抗，空気抵抗，回路に流れる電流がつくる磁場は無視をする．

時刻$t$における，斜面方向の移動距離$x$，導体棒の速度$v$，コンデンサーに蓄えられる電荷$Q$を求めよ．

<解答>

NEKO

時刻$t$における導体棒の速度を$v$，回路に流れる電流を$i$，コンデンサーに蓄えられている電荷を$Q$として，キルヒホッフの法則と導体棒の運動方程式を立てましょう．

導体棒の問題は次の3つの式を意識しましょう．

導体棒の問題で立てて欲しい3つの式

回路の式（オームの法則，コンデンサーの基本式，電荷保存則など）
導体棒の運動に関する式（つり合いの式，運動方程式，運動量保存則など）
導体棒と回路の系全体のエネルギー収支の式

NEKO

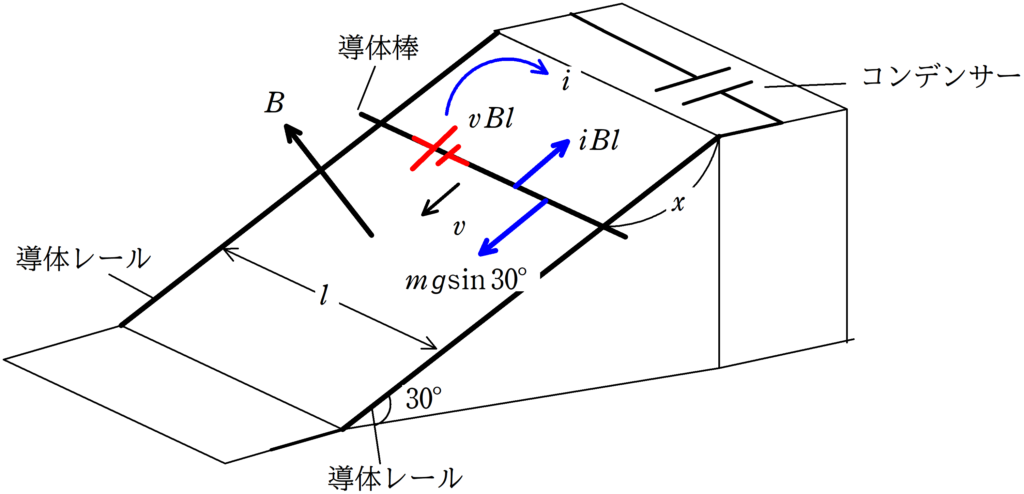
導体棒は磁場中を運動していると，電池になるんだったね．

次の式を確認しておこう！

導体棒に生じる誘導起電力の公式（直線運動）

PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，

$V=v_{\perp}Bl$

NEKO

今回は，速度$v$で磁束密度の大きさが$B$，長さ$l$の導体棒を考えているので，誘導起電力の大きさは$vBl$だね．

そして，コンデンサーの問題のときによく使うのは，次の2つの式だよ．

コンデンサーの基本式

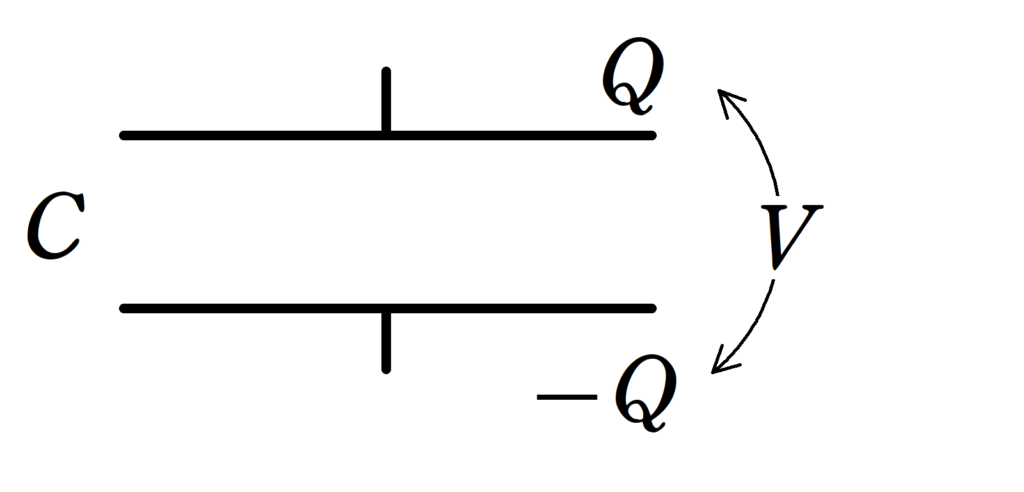
コンデンサーの電気容量（静電容量）を$C$，コンデンサーにかかる電圧を$V$，蓄えられた電気量を$Q$とすると，

$Q=CV$

の関係がある．

電流の定義

時間$\Delta t$の間に電気量$\Delta Q$が通過するときの電流の大きさ$i$は

$i=\dfrac{\Delta Q}{\Delta t}$

NEKO

それでは，回路の式から立てましょう．

コンデンサーにかかる電圧を$V_{\rm C}$として，キルヒホッフの法則を立てます．

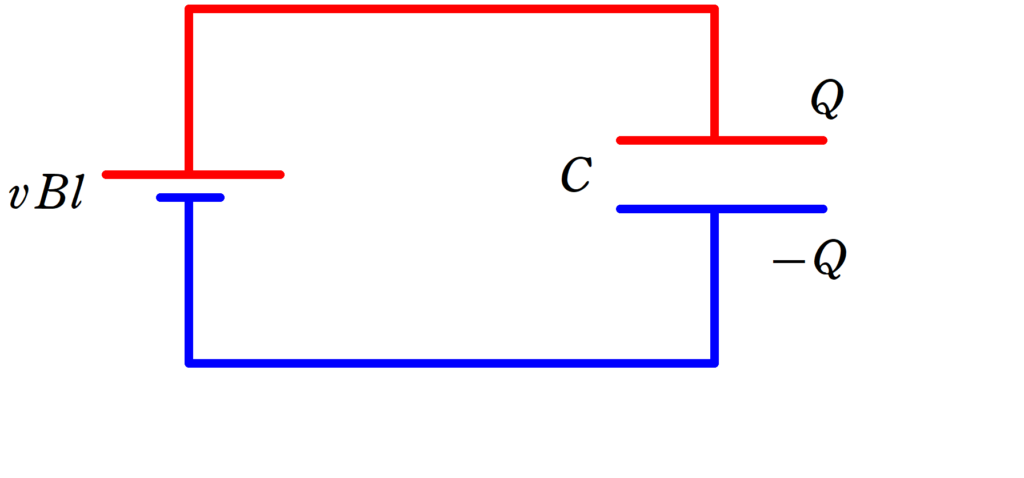
★　キルヒホッフの法則

$vBl-V_{\rm C}=0$　$\dots　(\ast)$

★　コンデンサーの基本式

$Q=CV_{\rm C}$　$\dots　(2\ast)$

$(\ast)$，$(2\ast)$より

$Q=CvBl$　$\dots　(3\ast)$

NEKO

さらに，導体棒の運動方程式を立てます．

導体棒は斜面方向に動いていますね．

斜面下向きに重力を分解した$mg\sin 30°$と，電磁力$iBl$が斜面上向きにかかります．

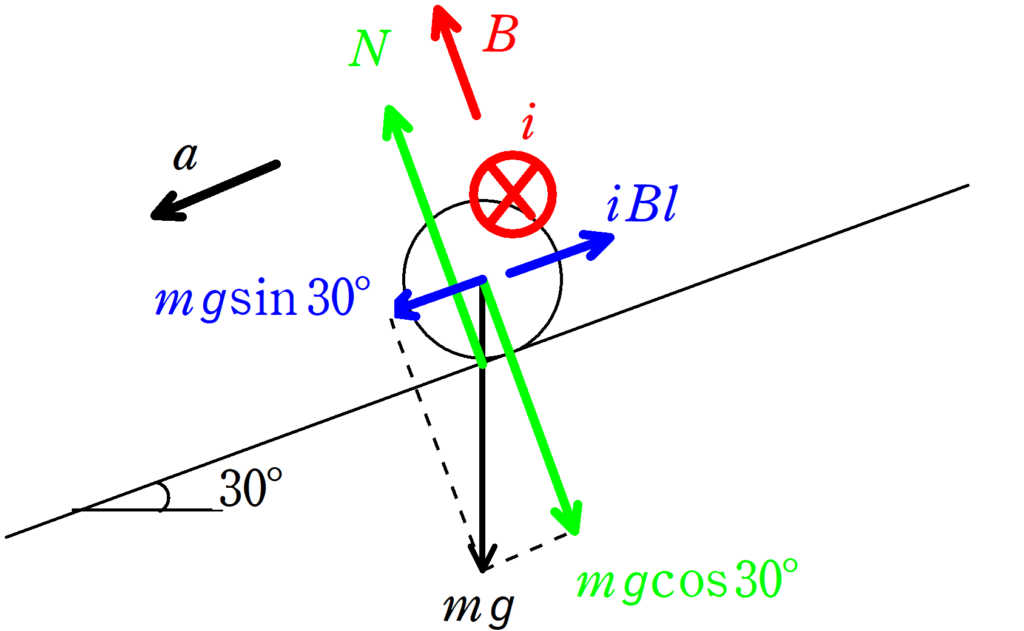
★　導体棒の運動方程式

$ma=mg\sin 30^{\circ}-iBl$　$\dots　(4\ast)$

一方，電流の定義式より

$i=\dfrac{\Delta Q}{\Delta t}$

これに，$(3\ast)$の$Q=CvBl$を代入して

$\eqalign{i&=\dfrac{\Delta}{\Delta t}(CvBl)\\&=CBl\dfrac{\Delta v}{\Delta t}\\&=CBla}$　$\dots　(5\ast)$

NEKO

上の式では，加速度の定義$a=\dfrac{\Delta v}{\Delta t}$を用いたよ．

さらに，$(5\ast)$を$(4\ast)$に代入してみよう．

$\eqalign{ma&=mg\sin 30°-CBla\cdot Bl\cr ma&=\dfrac{1}{2}mg-CB^{2}l^{2}a\cr (m+CB^{2}l^{2})a&=\dfrac{1}{2}mg\cr a&=\dfrac{mg}{2(m+CB^{2}l^{2})}}$

NEKO

上式の右辺は一定なので，導体棒は加速度$a=\dfrac{mg}{2(m+CB^{2}l^{2})}$の等加速度運動をすることがわかったね．

★　等加速度運動の式

等加速度運動の式より，時刻$t$における速度$v$は

$v=at=\dfrac{mg}{2(m+CB^{2}l^{2})}t$

時刻$t$における，移動距離$x$は

$x=\dfrac{1}{2}at^{2}=\dfrac{mg}{4(m+CB^{2}l^{2})}t^{2}$

また，$(3\ast)$の$Q=CvBl$に$v=\dfrac{mg}{2(m+CB^{2}l^{2})}t$を代入して

$Q=\dfrac{mgCBl}{2(m+CB^{2}l^{2})}t$

PHYさん

ちなみに，エネルギー収支の式として

$\dfrac{1}{2}mv^{2}-mgx\sin 30°+\dfrac{Q^{2}}{2C}=0$

が成り立っていますね．

この回路の場合普通の電池と違い少しずつ起電力が大きくなるので，誘導起電力がした仕事の分すべてがコンデンサーの静電エネルギーとして蓄えられます．

こちらの記事でも取り上げているので，興味がある人は読んでみてください．

また，次回の内容はこちらです．