
「電荷保存則演習」では,主に
・電荷保存則
・コンデンサーの式
・キルヒホッフ則
を立てることによって,問題を解いていきます.
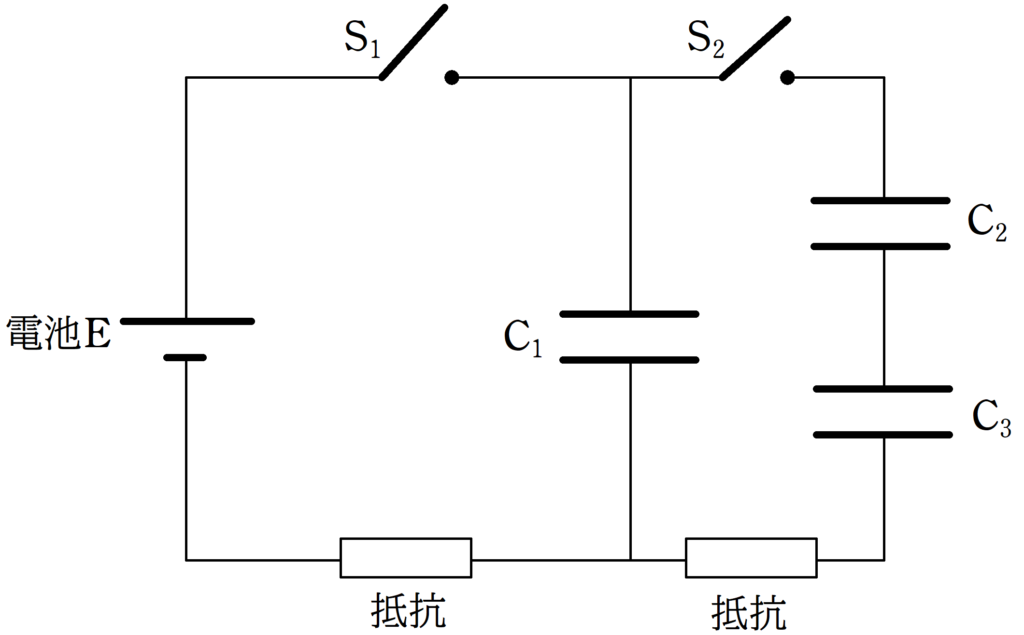
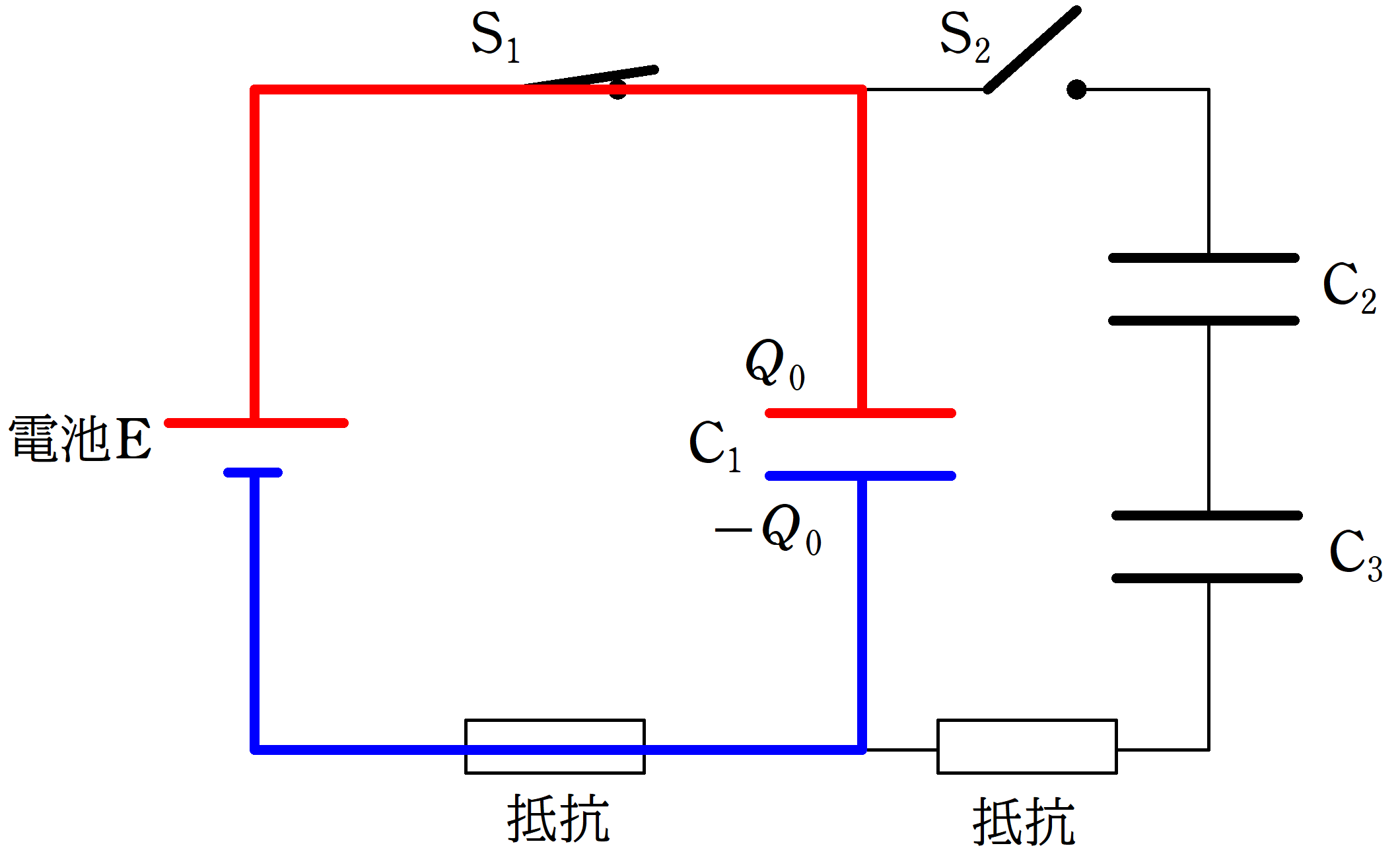
起電力$V$の電池と,スイッチ$\rm S_{1}$,$\rm S_{2}$,電気容量$C$,$2C$,$3C$のコンデンサー,$\rm C_{1}$,$\rm C_{2}$,$\rm C_{3}$と電気抵抗が上のように,接続されている.
すべてのコンデンサーには電荷が蓄えられていない状態から,スイッチ$\rm S_{1}$を閉じる.
(1) スイッチ$\rm S_{1}$を閉じて十分時間が経ったときのコンデンサー$\rm C_{1}$に蓄えられている電荷$Q_{0}$を求めよ.
(2) (1)の後,スイッチ$\rm S_{1}$を開いてからスイッチ$\rm S_{2}$を閉じた.
十分時間が経った後,コンデンサー$\rm C_{1}$,$\rm C_{2}$,$\rm C_{3}$に蓄えれている電荷$Q_{1}$,$Q_{2}$,$Q_{3}$を求めよ.
<解答>
(1)

はじめの問題はコンデンサーの式を用いて計算しましょう.
コンデンサー$\rm C_{1}$と電池の電圧は同じになるんだね.
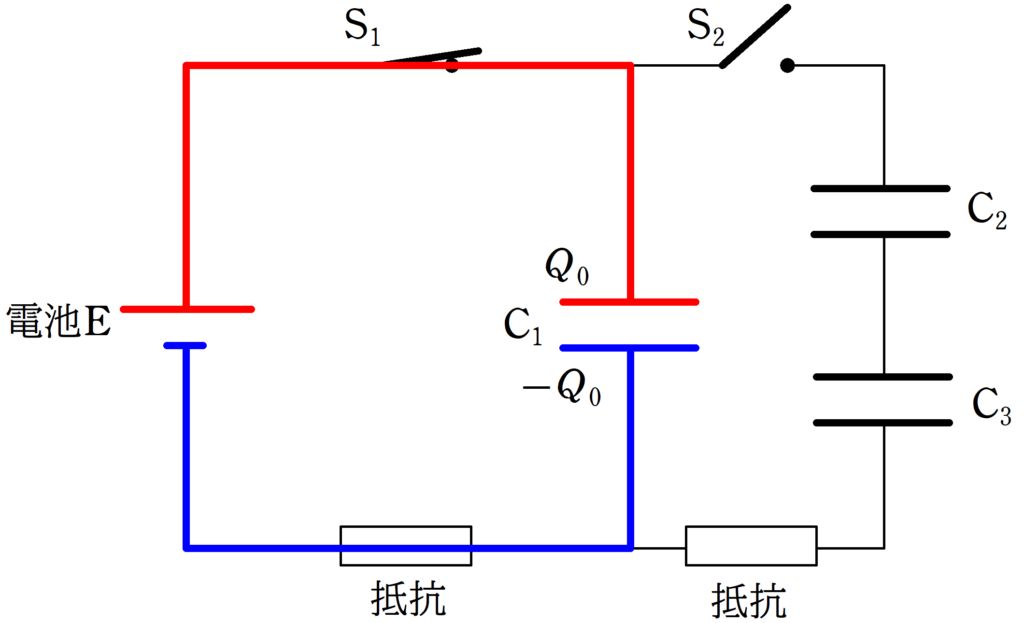
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
★ コンデンサーの式
$Q_{0}=CV$ (答)
(2)

次に,スイッチ$\rm S_{1}$を開いて,その後スイッチ$\rm S_{2}$を閉じます.
このとき,一般にコンデンサーに電荷$Q$が蓄えらえている際には,次のように,電位差が生じることがコンデンサーの式からも理解できます.
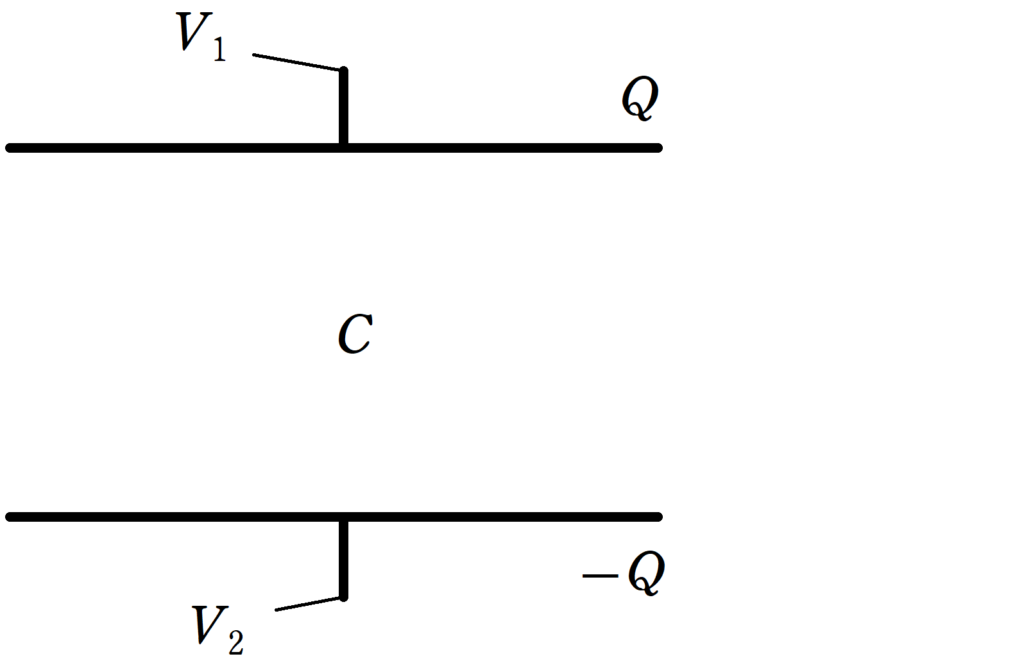
電気容量$C$のコンデンサーに,電荷$Q$が蓄えれている.
$+Q$側の極板の電位を$V_{1}$,$-Q$側の極板の電位を$V_{2}$とすると,コンデンサーの式より
$Q=C(V_{1}-V_{2})$
であるから,
$V_{1}-V_{2}=\dfrac{Q}{C}$
の電位差が生じている.

合わせて電荷保存則も立式します.
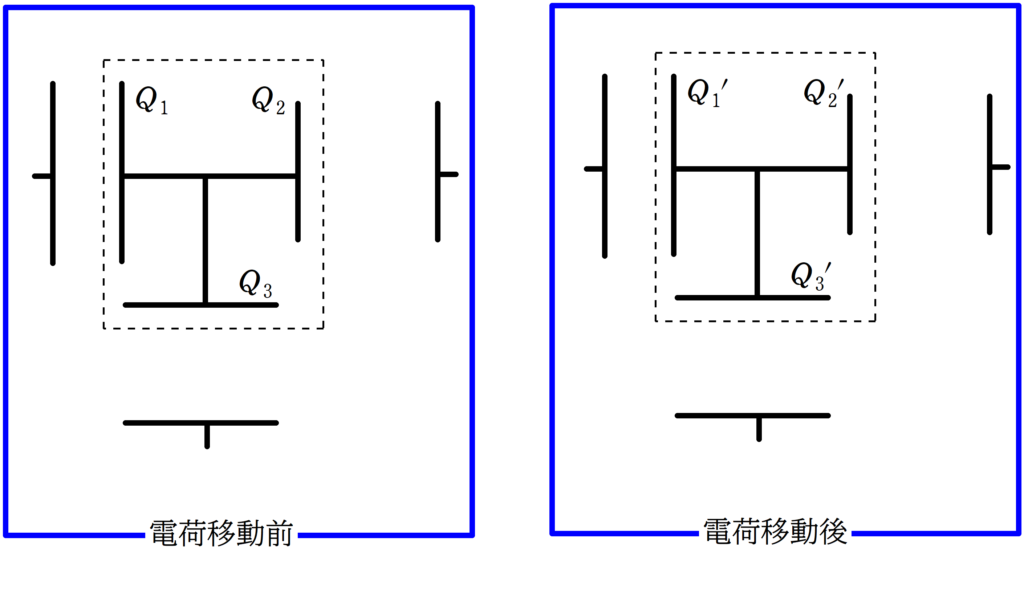
孤立した部分の電荷の総和は変化しない.これを電荷保存則という.
たとえば,上図のように点線部分の孤立した場所の電荷について考えると
$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$
が成り立つ.

電荷保存則は下図の①部分と②部分で立てましょう.
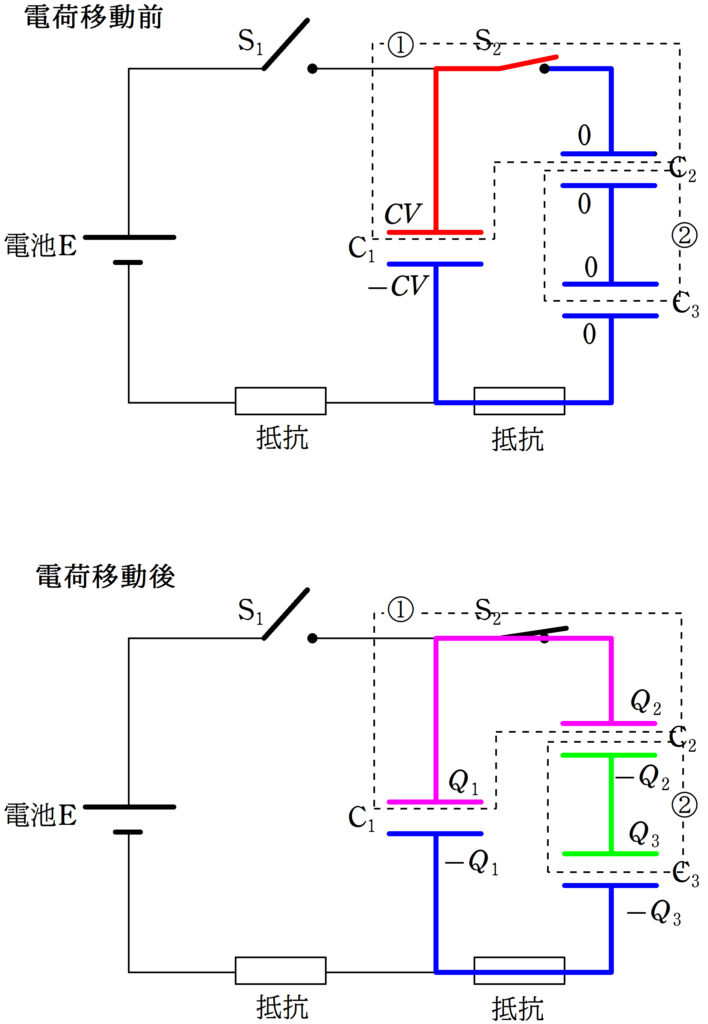
★ ①と②部分の電荷保存則
$Q_{1}+Q_{2}=Q_{0}=CV$ $\dots (\ast)$
$-Q_{2}+Q_{3}=0$ $\dots (2\ast)$
★ キルヒホッフ則
上図の青い部分を電位の基準として,ピンク→緑→青で電位を追うと
$\dfrac{Q_{1}}{C}-\dfrac{Q_{2}}{2C}-\dfrac{Q_{3}}{3C}=0$
両辺$6C$をかけて
$6Q_{1}-3Q_{2}-2Q_{3}=0$ $\dots (3\ast)$
また,$(\ast)$,$(2\ast)$より
$Q_{2}=Q_{3}=CV-Q_{1}$ $\dots (4\ast)$
$(4\ast)$を$(3\ast)$に代入して
$6Q_{1}-3(CV-Q_{1})-2(CV-Q_{1})=0$
$\therefore Q_{1}=\dfrac{5}{11}CV$
$(4\ast)$より
$Q_{2}=Q_{3}=CV-\dfrac{5}{11}CV=\dfrac{6}{11}CV$
以上より,$Q_{1}=\dfrac{5}{11}CV$,$Q_{2}=Q_{3}=\dfrac{6}{11}CV$

コメント
[…] […]
[…] […]