
今回より,熱気球の問題演習をします.
次の記事でも説明にある.「熱気球でよく使う式」を用いて計算します.
理想気体の圧力を$P$,絶対温度を$T$,密度を$\rho$とする.このとき,理想気体の分子量が変化しなければ次の式が成り立つ.
$\dfrac{P}{\rho T}=$一定

また,気球は非常に大きく,まわりの空気が気球をおす力(浮力)がかなり大きくなります.
浮力は次の記事でも説明しています.
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.

これらをふまえて次の問題を解いてみましょう.
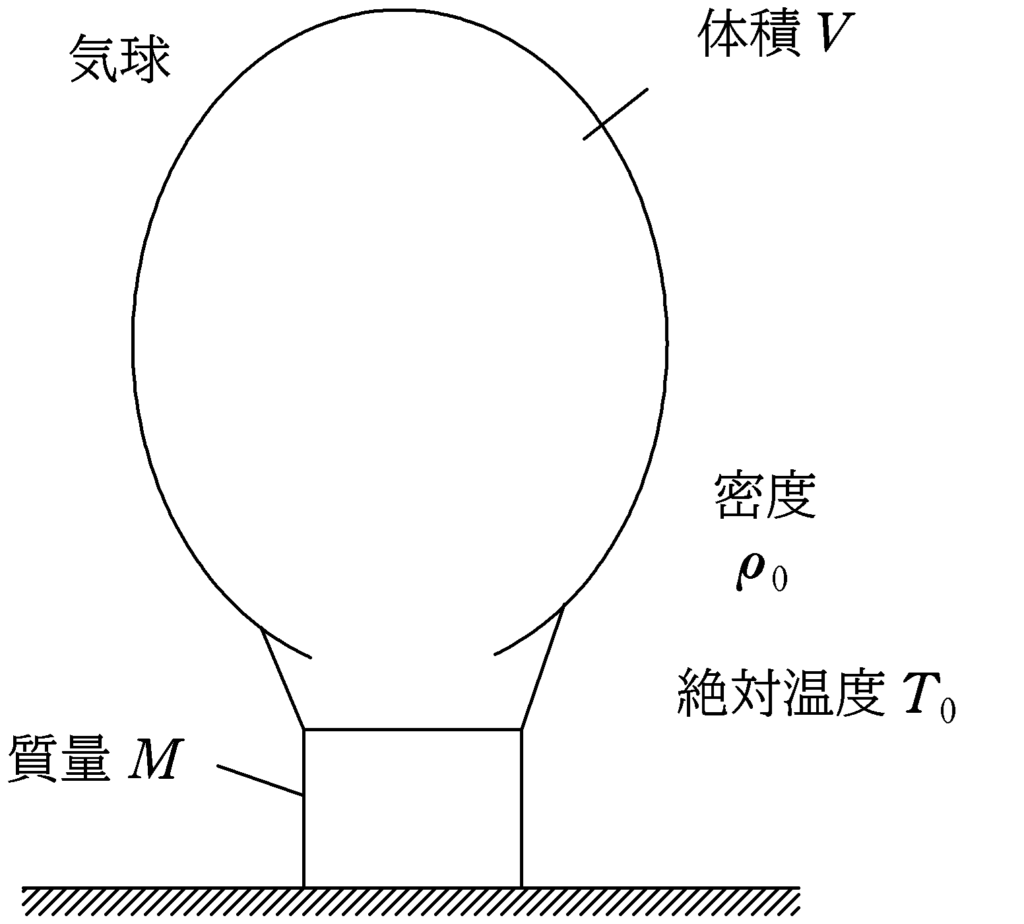
地上に質量$M$の熱気球が置かれている.熱気球の空気を入れる部分の体積は$V$である.また,地上における空気の密度を$\rho_{0}$,絶対温度を$T_{0}$とする.熱気球内の空気と地上における空気は自由に出入りできるようになっているため,気球内の圧力は地上の圧力と同じである.以下,空気は理想気体と考えることができる.熱気球内の空気を熱していくと,絶対温度が$T$になったときに気球は浮かび上がった.重力加速度の大きさを$g$として,浮かびあがったときの絶対温度$T$を求めよ.
<解答>

熱気球の問題では,
- つり合いの式
- ボイル・シャルルの法則(熱気球で使いやすい形に変形した$\dfrac{P}{\rho T}=一定$の式)
の式を立てていきます.
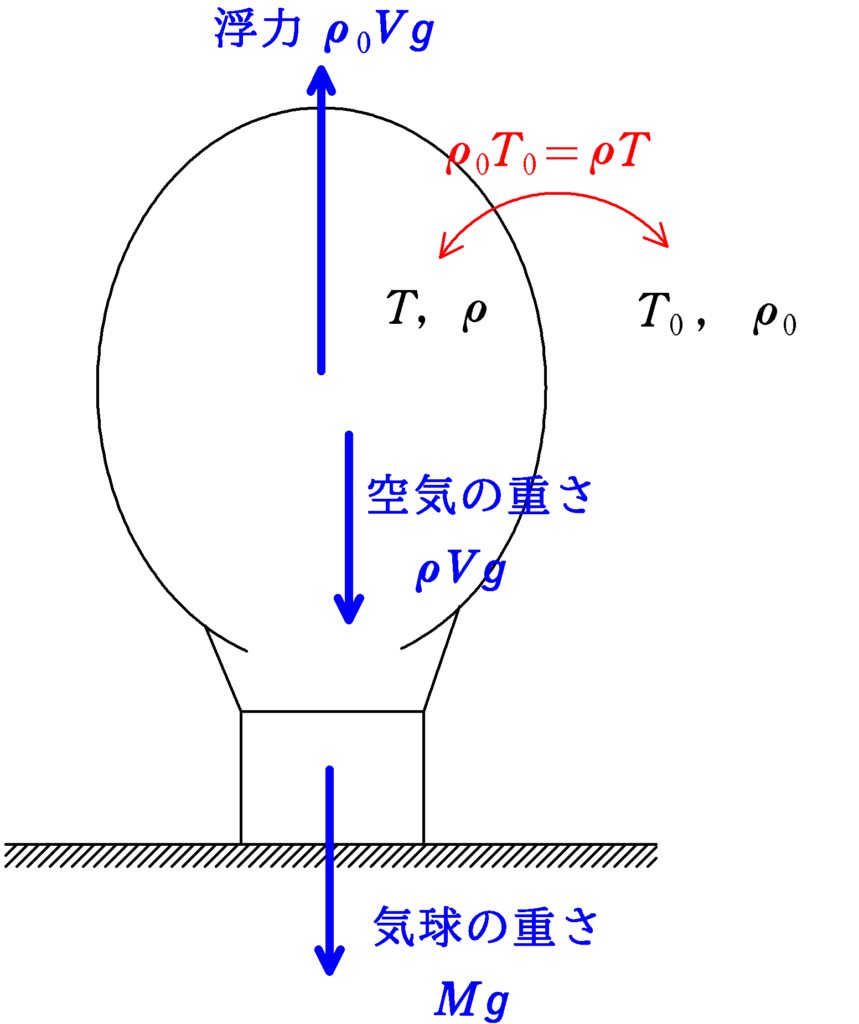

気球内の絶対温度を$T$,密度を$\rho$とします.
上図のように,気球の重さは$Mg$,気球内の空気の重さは$\rho Vg$,浮力の大きさは$\rho_{0}Vg$となります.
この式をみると,浮力$\rho_{0}Vg$の$\rho_{0}$は気球内の空気を熱する前も後も変化しません.($\rho_{0}$は気球外の密度.そもそも浮力はまわりの空気が押す力の和なので,気球内の空気を熱しても変化しません.)
熱気球は,気球内の空気を熱することで,「浮力が大きくなるから浮く」のではなく,「気球内の空気が軽くなるから浮く」のです.
★ 熱気球のつり合いの式
$Mg+\rho Vg=\rho_{0}Vg$
$\therefore\,\, M+\rho V=\rho_{0}V$ $\cdots (\ast)$

また,$\dfrac{P}{\rho T}=一定$は分子量が変化しなければどこでも成り立ちます.
熱気球内外でこの式を立てましょう.この際,問題文に書かれているように圧力は気球内外で同じなので,実質$\rho T=一定$が成り立ちます.
★ $\dfrac{P}{\rho T}=一定$の式
$\rho T=\rho_{0}T_{0}$
$\rho =\dfrac{\rho_{0}T_{0}}{T}$ $\cdots (2\ast)$

$(2\ast)$の式は$T$(気球内の温度)が大きくなると,$\rho$(気球内の密度)が小さくなることを示しています.つまり,温度が高くなると,気球内の空気が追い出されて軽くなるわけです.
$(2\ast)\to (\ast)$に代入して,$T$を求めます.
$(2\ast)\to (\ast)$
$\eqalign{M+\dfrac{\rho_{0}T_{0}}{T}\times V&=\rho_{0}V\cr \dfrac{\rho_{0}T_{0}V}{T}&=\rho_{0}V-M \cr \therefore\,\, T&=\dfrac{\rho_{0}T_{0}V}{\rho_{0}V-M}}$ (答)

次回の内容はこちらです.




コメント