
今回は,よくある間違いシリーズです.
次の問題をみてみましょう
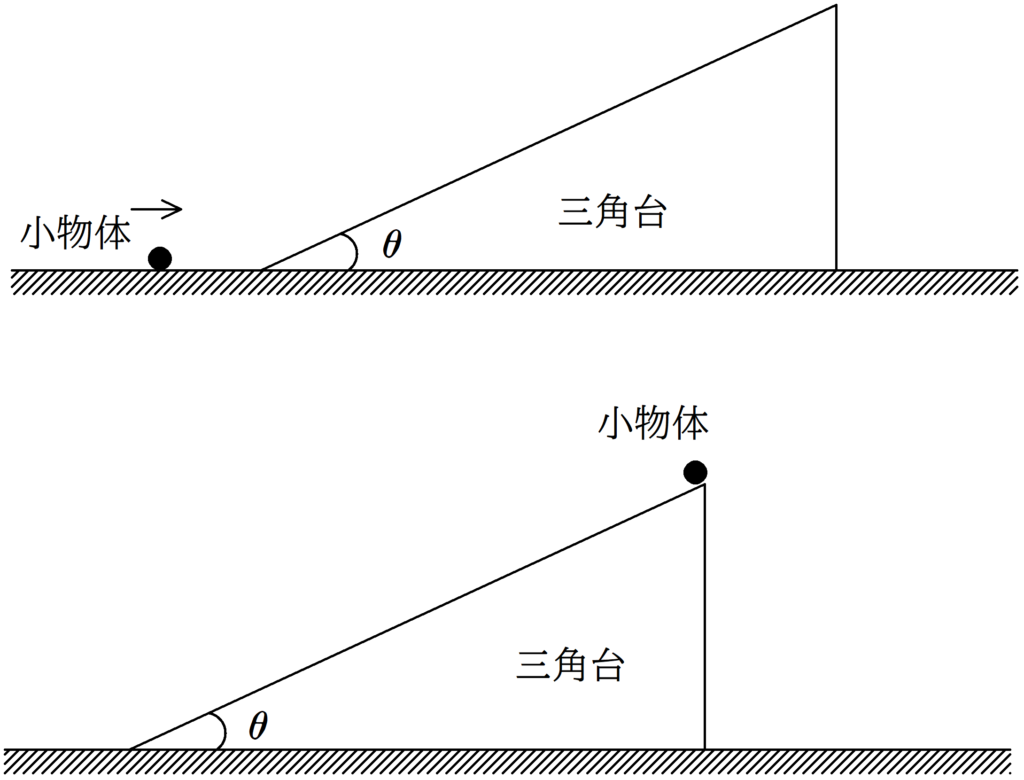
なめらかな水平面の上に傾角$\theta$の斜面をもつ三角台がおかれていて,水平方向に自由に動くことができる.
水平面にある小物体に初速を与えたところ,小物体は三角台の斜面上をのぼり,斜面の最高点から飛び出した.
このとき,水平右向きと鉛直上向きを正とし,$v_{x},v_{y},V>0$とすると,静止した床の上からみた小物体の水平方向の速度が$v_{x}$,鉛直上方向の速度が$v_{y}$であった.
また,三角台の水平速度は$V$であった.
$\tan \theta$を$v_{x}, v_{y} , V$を用いて表せ.
<解答>

この文章から察するに
$\tan\theta=\dfrac{v_{y}}{v_{x}}$ではないんだよね??

そうですね.
それがよくある解答ミスです.
三角台からみた小物体の飛び出す角度は,水平面からなす角$\theta$ですが,静止した人からみた角度は$\theta$ではありません.

なんとなく同じような気がするんだけど・・・

では,相対速度の復習をしましょう.
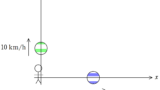
次図のように,静止したAから電車をみると速度が$5.0\rm m/s$でした.
また,電車の中にいるBから見ると小物体の速度が水平方向に$2.0\rm m/s$でした.
それでは,Aからみた小物体の速度はいくらでしょう.
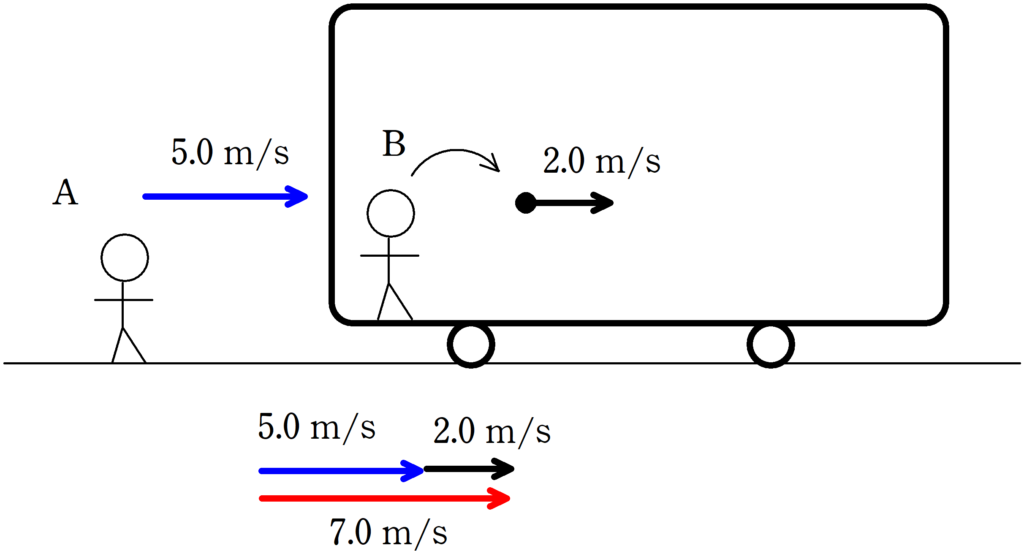

$5.0+2.0=7.0\rm m/s$だね!

それでは,電車の中にいるBからみて,水平速度の他に鉛直上向きにも速度$2.0\rm m/s$をもっている場合はどうでしょうか?
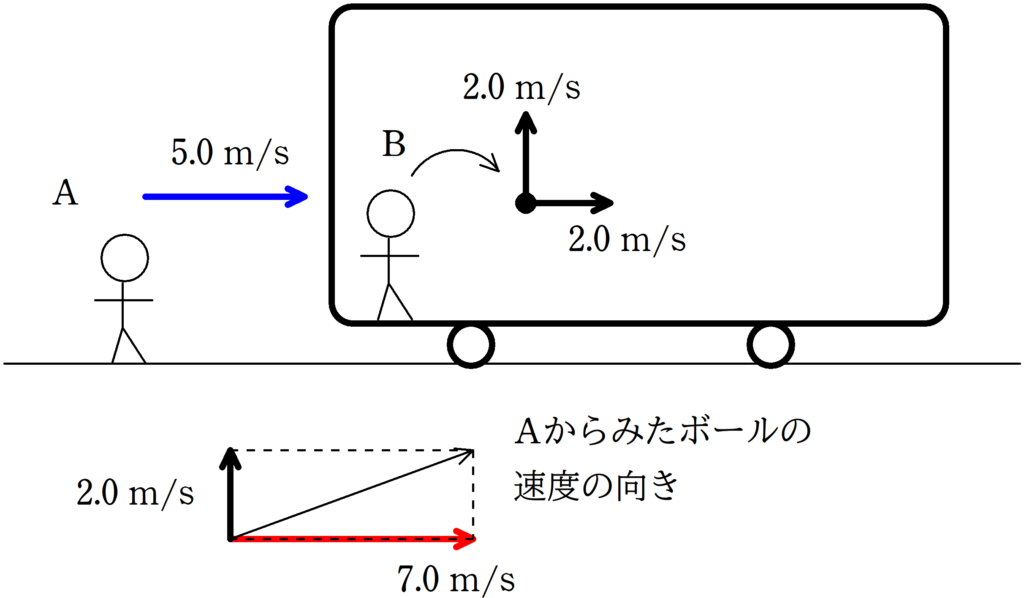

Aからみると水平方向の速度が$7.0\rm m/s$,鉛直方向の速度が$2.0\rm m/s$だね.

そうですね.
電車の中にいるBからみると,45°の角度の方向に速度をもっていますが,Aからみると45°よりやや引く角度の速度になっているのが確認できますね.
そもそも,速度は大きさだけなく,向きの情報もあるんです.
見る人によって変化するのは,速度の大きさだけではなく,向きも変化します.

そっか!
角度が変わるのは変だと思ったけど,見る人によって速度の向きが変わると考えると当たり前だね.
ちなみに,相対速度については,こちらの記事を参考にしてね!

それでは本題にはいりましょう.
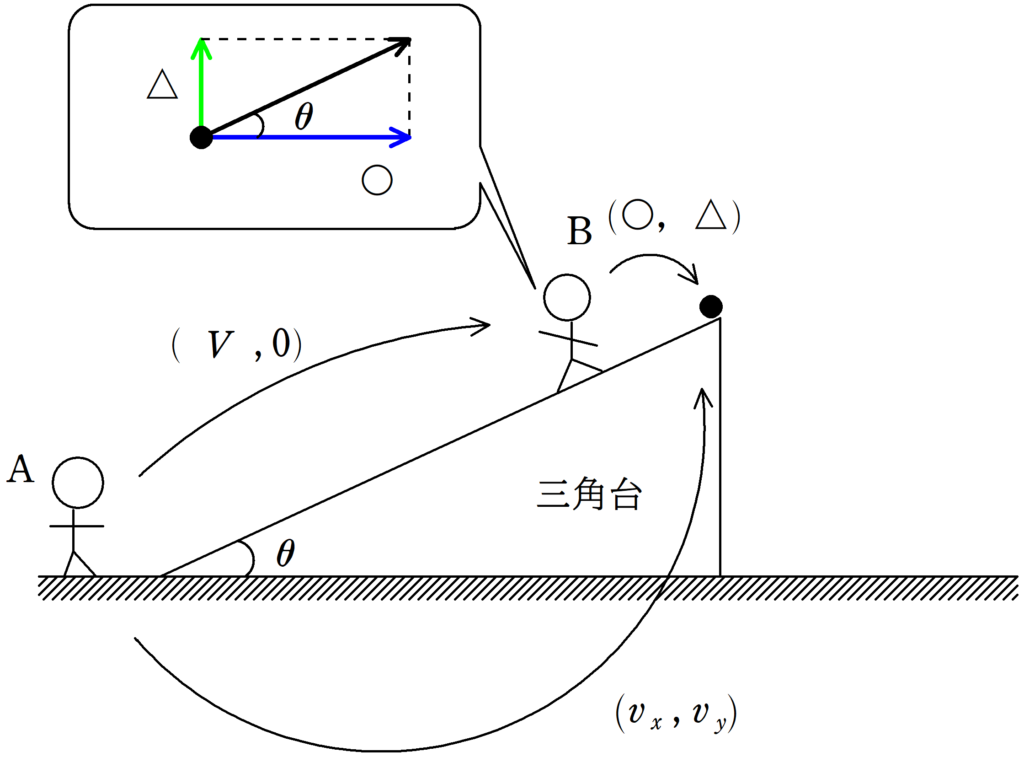

Aからみた三角台の速度が$(V , 0)$,Aからみた小物体の速度が$(v_{x},v_{y})$なので,三角台で静止しているBくんからみた小物体の速度$(〇, △)$は次のようになるね.
$(V , 0)+(〇 , △)=(v_{x} , v_{y})$
$\therefore (〇 , △)=(v_{x} , v_{y})-(V , 0)=(v_{x}-V , v_{y})$
したがって,
$\tan \theta =\dfrac{v_{y}}{v_{x}-V}$

ちなみに,静止したAからみた小物体の水平からのなす角を$\alpha$とすると,$\tan \alpha$はどのようになりますか??

Aからみた速度を考えればいいんだから
$\tan\alpha =\dfrac{v_{y}}{v_{x}}$
だね.

その通りです.
では最後にまとめです.
観測者によって速度の大きさや向きは異なって見える.
したがって,物体の進む向きも観測者によって異なる.
物体の進む方向が問われたとき,誰から見た方向を聞かれているのかを確認すること.

コメント
[…] [よくある間違い]動く斜面から飛び出す物体の軌道のなす角 […]
[…] […]
物理学科院卒です。問題のような状況で三角台が左に運動するようなことは無いと思うのですが…前提がおかしくないですか?
ご指摘ありがとうございます。
設定ミスですね。
これから訂正します!
運動量保存から考えても、もし飛び出すときに台が左向きの運動量をもつのなら、小球は元々持っていた右向きの運動量よりも大きい運動量を右向きに持つことになります。つまり台を登ったことで小球は右向きに加速したことになりおかしいです。