
ローレンツ力によってらせん運動をする問題は,3次元の運動であることもあって,難しいね.
今回は,らせん運動の問題ですべきについて話をするよ.
★ ローレンツ力によるらせん運動ですべきこと
1. 直線運動している成分と円運動している成分の見極め.
2. 円運動の運動方程式,周期の式を立てる.
3. 直線運動している方向の速度成分と円運動の周期からピッチを計算する.

上の3つのことを次の問題を通して解説していきましょう.
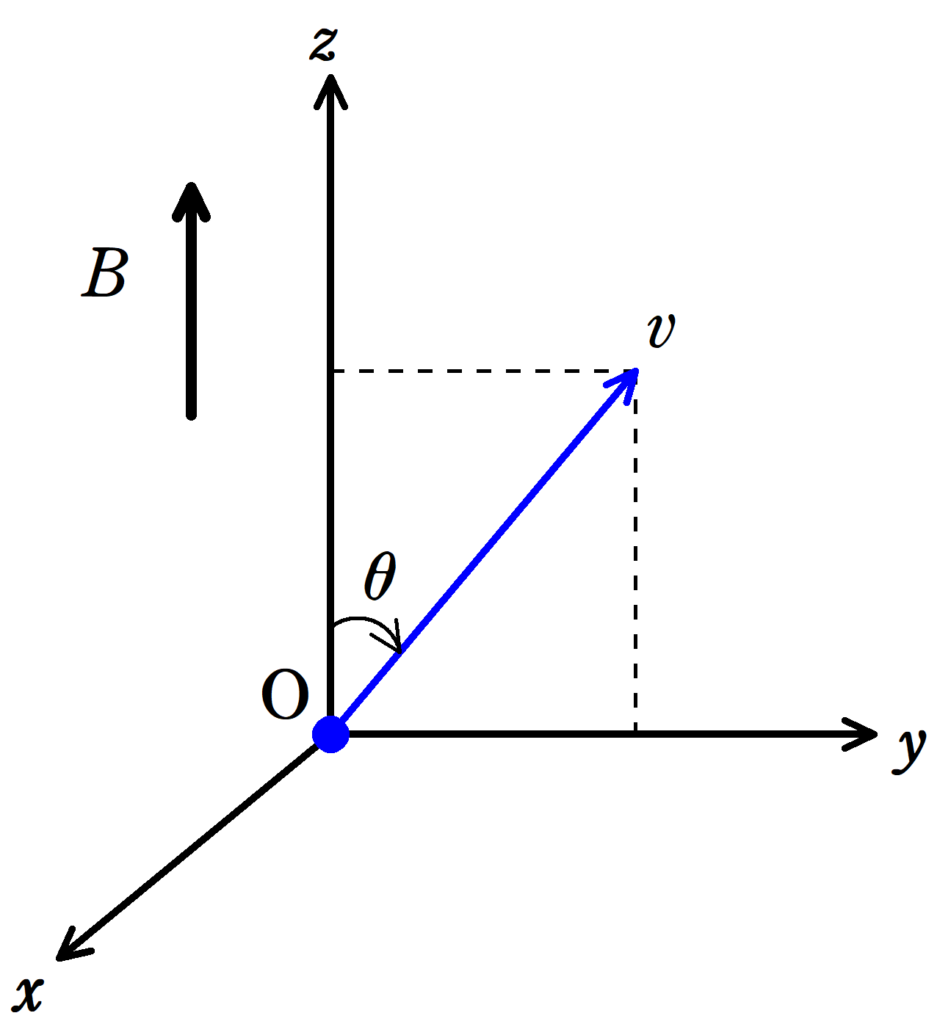
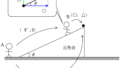
上図のような$xyz$直交座標がとられている.
この空間には$z$軸の正の方向に一様な磁場がかけられており,その磁束密度の大きさは$B$である.
いま,原点$\rm O$にて,質量$m$,電荷$q(q>0)$の荷電粒子を,$yz$平面の$z$軸の正の方向から$\theta$のなす角に初速$v$を与えたところ,荷電粒子はらせん運動をした.
荷電粒子が運動を開始してから再び$z$軸に戻ってきたときの$z$座標を求めよ.
ただし,重力の影響は無視する.
<解答>

まず,「1. 直線運動している成分と円運動している成分の見極め.」をしなくちゃね.
どうやって見極めればいいんだろう??

磁場の方向にはローレンツ力がかかりません.
その結果,ローレンツ力以外の力がはたらかない場合は,磁場の方向に等速度運動をします.
そして,等速度運動に垂直な平面で等速円運動を行うのです.
磁場の方向→等速度運動
磁場の方向と垂直な平面→等速円運動

じゃあ,まずは磁場の方向とそれに垂直な方向に速度を分解するんだね!
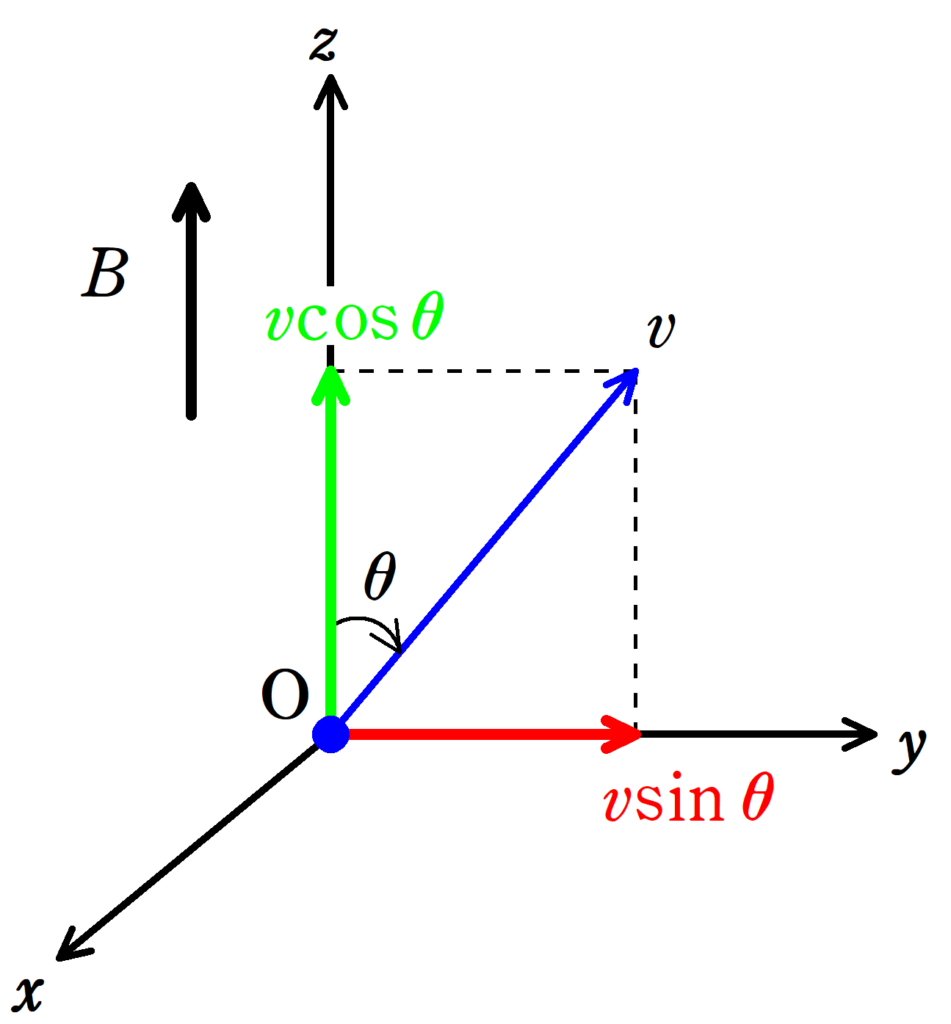

初速を$z$成分と$y$成分に分けると,それぞれ$v\cos\theta$,$v\sin\theta$となります.

つまり,磁場と同じ方向である,$v\cos\theta$が等速度の成分で,それに垂直な成分$v\sin\theta$が円運動の成分なんだね.

そうですね.
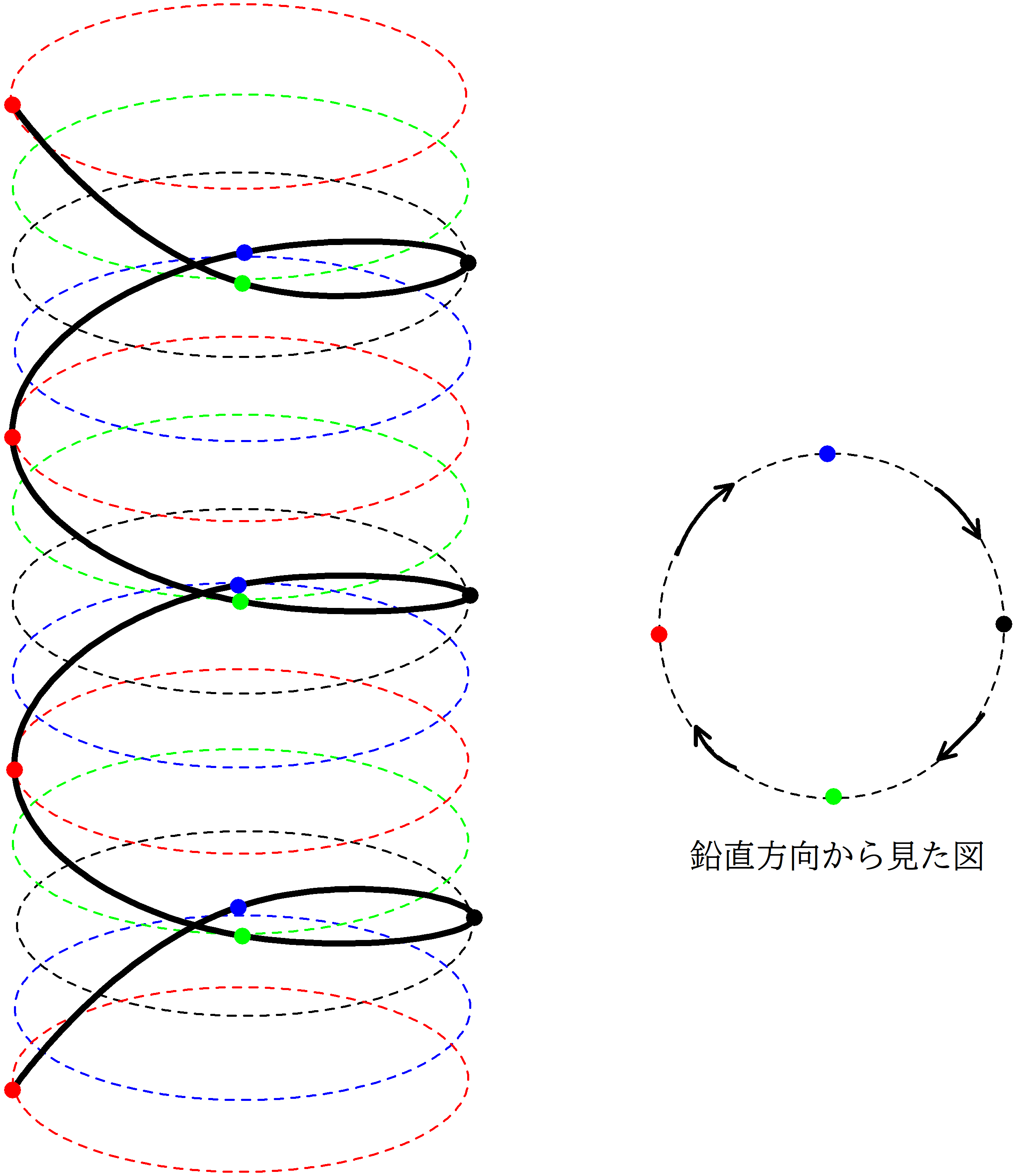
具体的な計算に入る前に,らせん運動の図を見てみましょう.
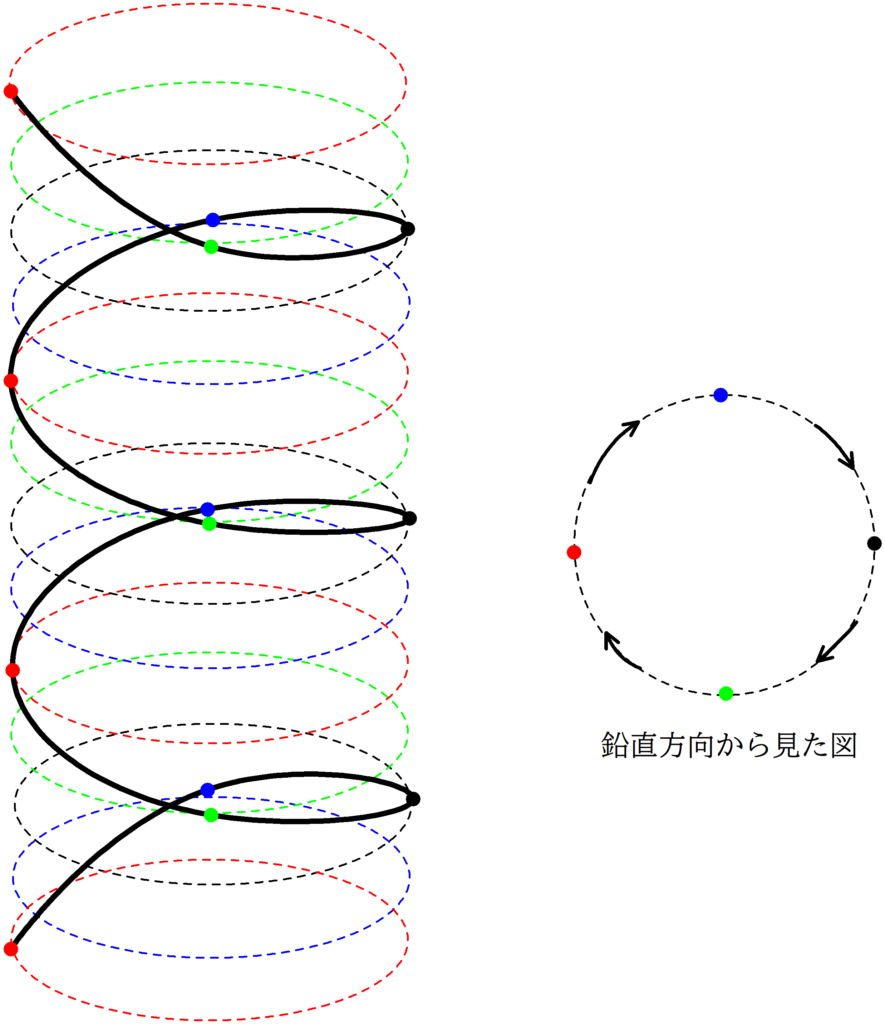

赤い点の部分だけみると,$z$軸の方向に等間隔だから,等速度運動しているんだね.
他の点も同じ.ちなみに,この赤い点と赤い点の距離をピッチというんだね.

はい.そして,$z$軸の正方向からみると,等速円運動をしているように見えるわけです.
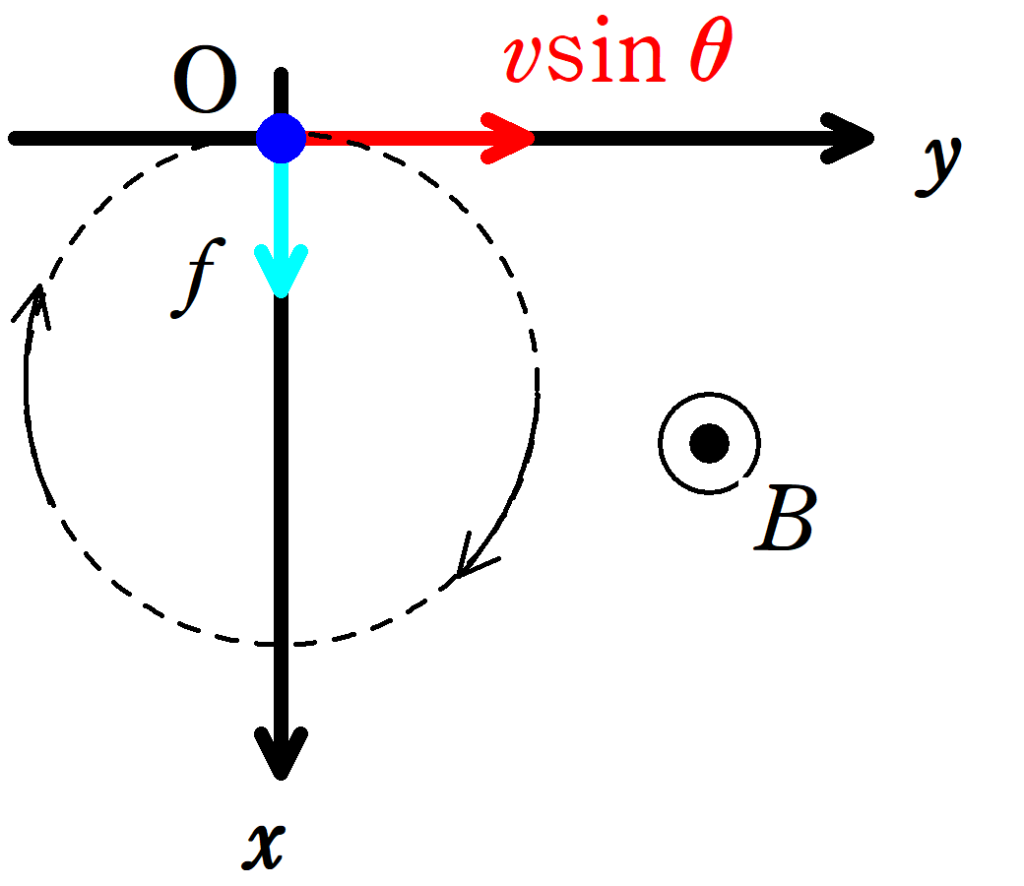

では,具体的な計算に入りましょう.
等速円運動の成分は
・運動方程式
・周期の式
を立てましょう.
磁場の大きさを$B$,磁場に垂直な速度の大きさを$v$,荷電粒子の電荷を$q$のとき,荷電粒子が受けるローレンツ力の大きさ$f$は
$f=|q|vB$
向きはフレミング左手の法則に従う.
$\clubsuit$フレミング左手の法則$\clubsuit$
親指→ローレンツ力の向き
人差し指→磁場の向き
中指→電流の向き(正電荷の動く向き,負電荷の動く向きと逆)
円運動の半径を$r$,周期を$T$とします.
★ 運動方程式
$m\dfrac{(v\sin\theta)^{2}}{r}=qv\sin\theta B$
$\therefore r=\dfrac{mv\sin\theta}{qB}$ $\dots (\ast)$
★ 円運動の周期の式
$T=\dfrac{2\pi r}{v\sin\theta}$ $\dots (2\ast)$
$(\ast)$を$(2\ast)$に代入して
$\eqalign{T&=\dfrac{2\pi}{v\sin\theta}\cdot \dfrac{mv\sin\theta}{qB}\\&=\dfrac{2\pi m}{qB}}$

ピッチは,円運動1周したときの$z$方向に進んだ距離です.
時間$T=\dfrac{2\pi m}{qB}$の間に速さ$v\cos\theta$で等速度運動しているので,$z$軸方向の移動距離$l$は次のようになります.
$l=v\cos\theta \cdot T=\dfrac{2\pi mv\cos\theta}{qB}$

ということで,答えは,$\dfrac{2\pi mv\cos\theta}{qB}$です!


コメント