<問題>
※三角台Qと水平面も常に接しているとしてください.
<解答>
球Pと壁(または斜面),球Pと三角台Qが常に接している条件(束縛条件)から移動距離の比を求め,移動距離の比が速さの比であることを利用して問題を解きます.
図1の解答
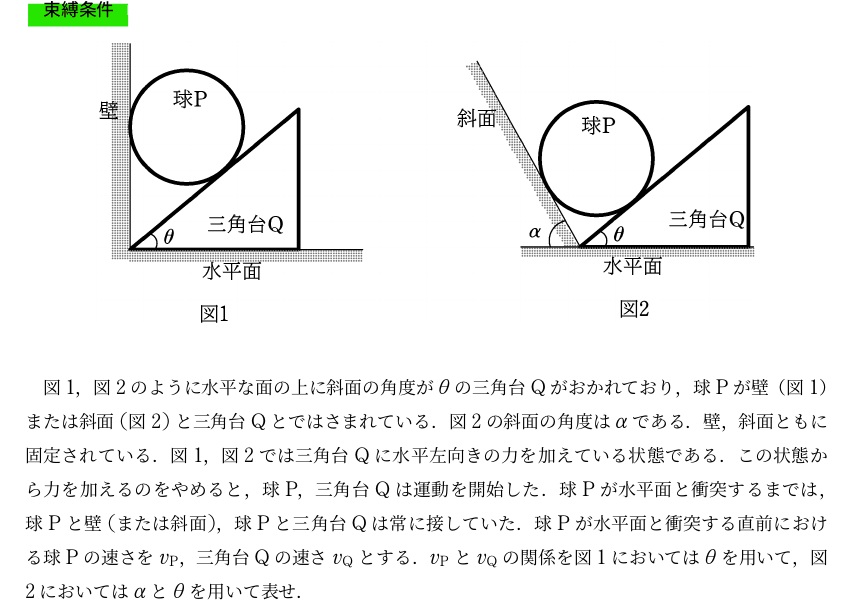
上図の点線は移動前,太青線は移動後の球P,太緑線は移動後の三角台Qです.
球Pは壁と常に接しているという条件から鉛直下方向に移動し,三角台は水平面と接しているので水平右方向へ移動します.
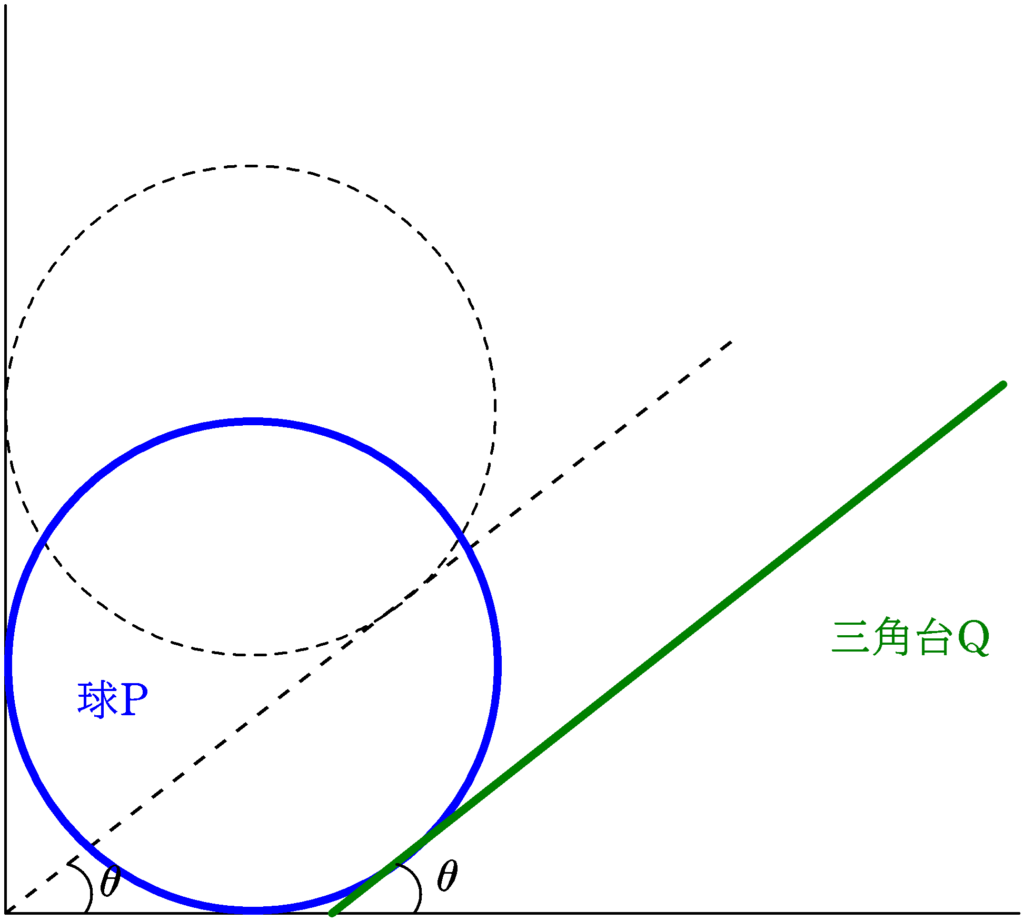
三角台Qは上図のOからAまでの矢印分移動しています.この移動距離を$x_{\rm Q}$としましょう.
さらに,球Pと三角台Qの接触点に着目します.移動前の接触点が上図のB,移動後の接触点はCです.
球Pが鉛直下方向に移動しているので接触点も鉛直下方向に移動しています.
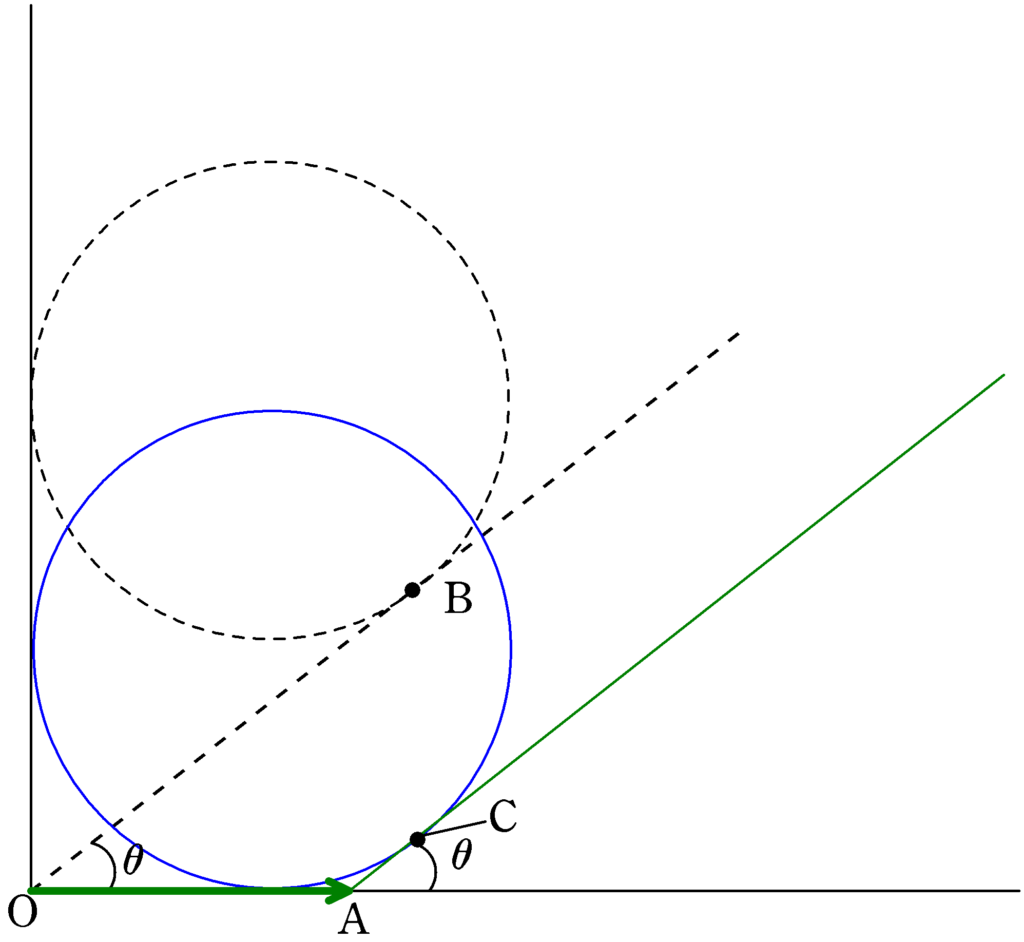
上図のようにAから鉛直方向に線を引いて,移動前の三角台の斜面との交点をDとします.BCとDAが平行(どちらも鉛直方向だから)で,DBとACも平行(どちらも三角台の斜面だから)なので,四角形ACBDは平行四辺形です.
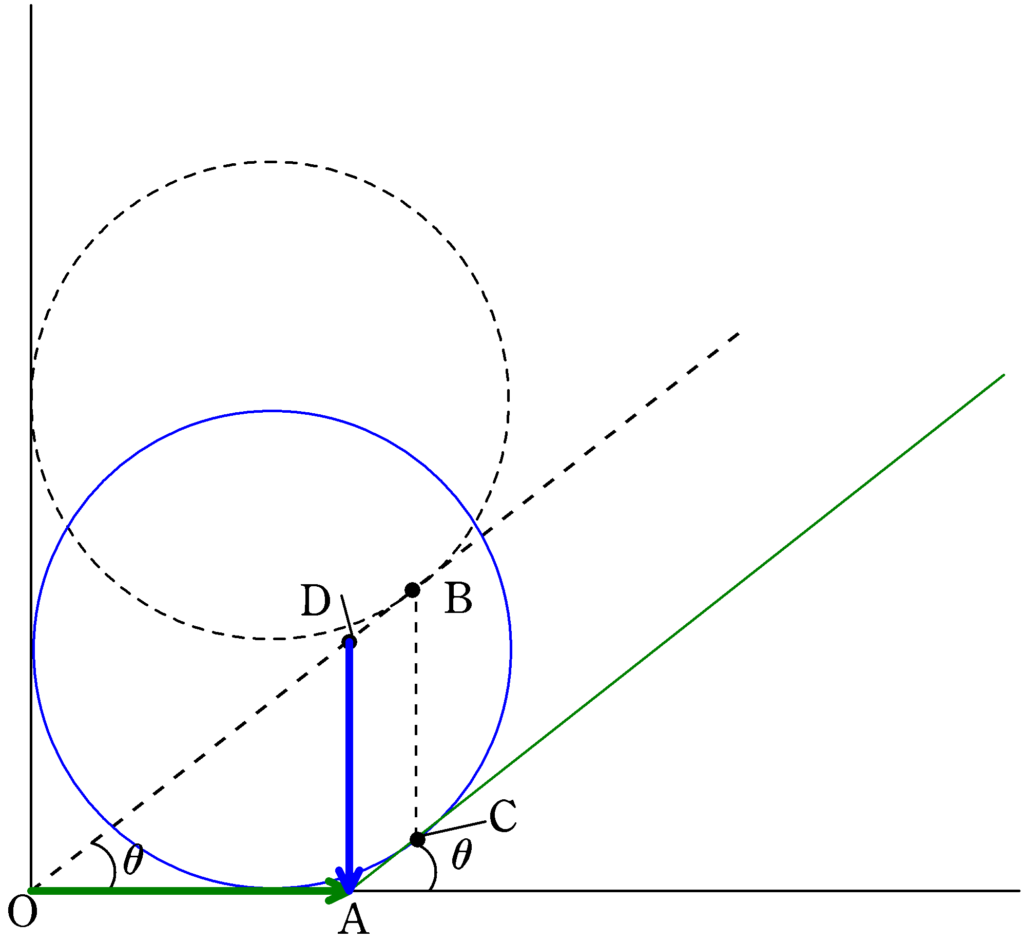
BCの移動距離分が球Pの移動距離であり,ACBDは平行四辺形なので,球Pの移動距離はDAの矢印の移動距離とも言えます.この移動距離を$x_{\rm P}$としましょう.
直角三角形OADに着目するとOAの長さを$x_{\rm Q}$としたので
$x_{\rm P}=x_{\rm Q}\tan\theta$
となり,移動距離の比は速さの比に等しいことから$v_{\rm P}$と$v_{\rm Q}$は
$v_{\rm P}=v_{\rm Q}\tan\theta$ (答)
の関係が成り立ちします.
図2の解答
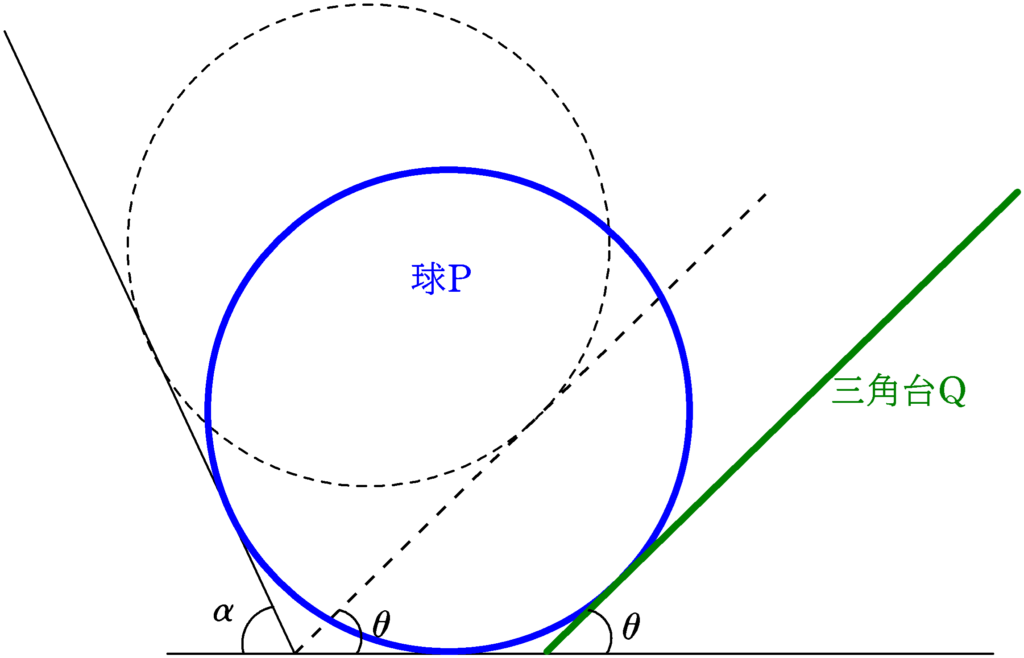
図1の解答の場合と同様に,点線が移動前,太青線が移動後の球P,太緑線が移動後の三角台Qです.
球Pは角度$\alpha$の斜面と接しているので斜面と平行な方向に移動し,三角台Qは水平面と接しているので水平右向きに移動します.
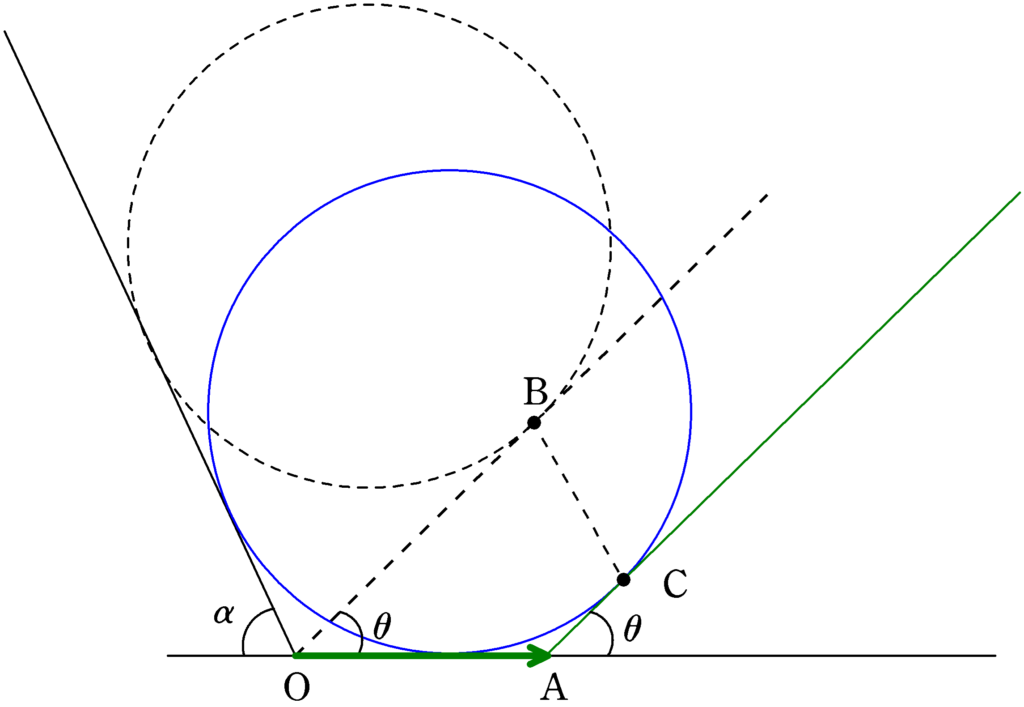
上図のOからAに引いた緑線の矢印が三角台の移動方向となります.この移動距離を$x_{\rm Q}$としましょう.
Bは移動前の球Pと三角台の接触点で,Cは移動後の接触点です.球が斜面と接しながら移動しているので,線分BCは斜面に平行な方向です.
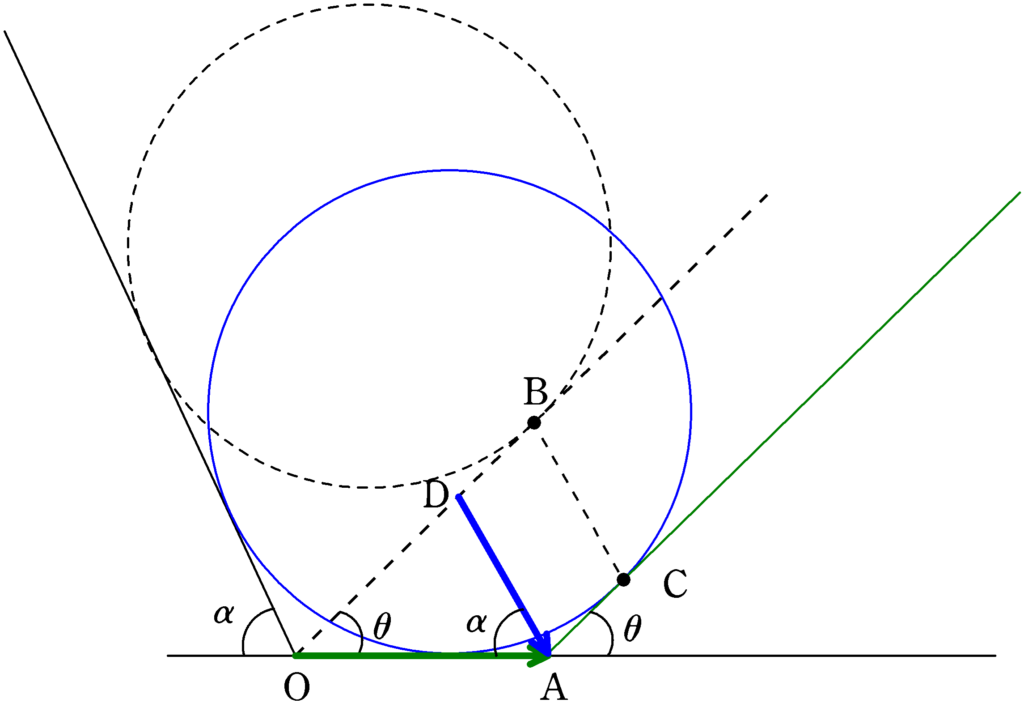
Aを通り線分BCに平行な直線を引き,移動前の三角台Qの斜面との交点をDとすると,四角形ACBDは平行四辺形となります.BCの長さ分が球Pの移動距離なので,DAが球Pの移動距離とも言えます.この移動距離を$x_{\rm P}$としましょう.
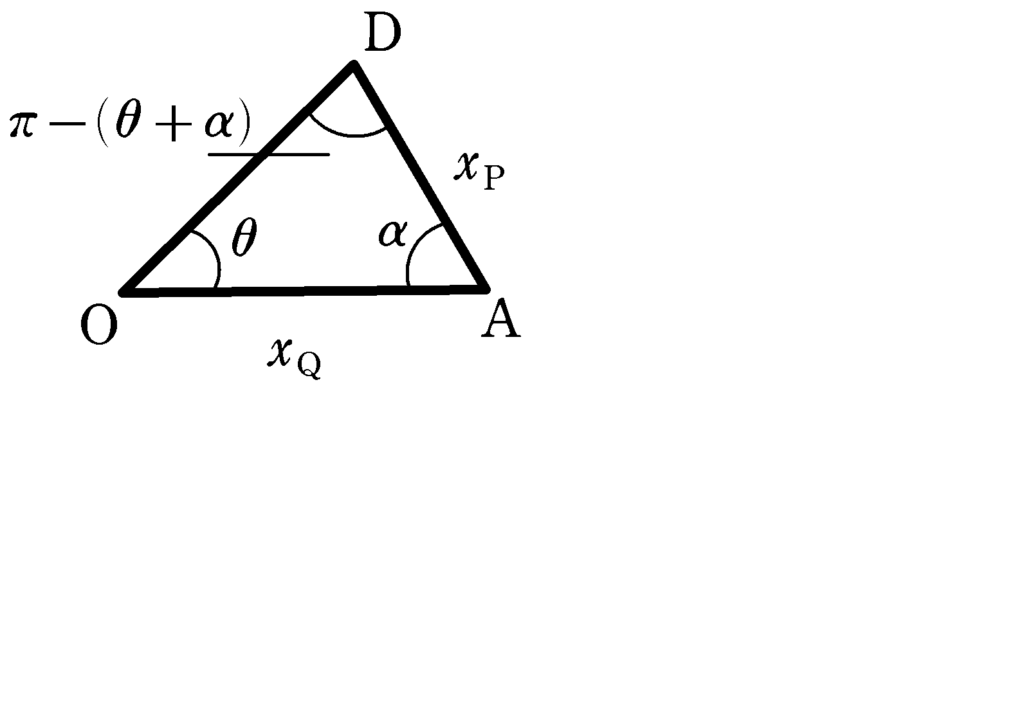
三角形OADに着目します.三角形の内角の和が$\pi$であることから,$\angle{\rm ODA}=\pi-(\theta+\alpha)$です.
正弦定理より
$\dfrac{x_{\rm Q}}{\sin(\pi-(\theta+\alpha))}=\dfrac{x_{\rm P}}{\sin\theta}$
$\sin(\pi-(\theta+\alpha))=\sin(\theta+\alpha)$より
$x_{\rm P}=\dfrac{\sin\theta}{\sin(\theta+\alpha)}x_{\rm Q}$
なので,速さ$v_{\rm P},v_{\rm Q}$の関係は
$v_{\rm P}=\dfrac{\sin\theta}{\sin(\theta+\alpha)}v_{\rm Q}$ (答)
相対変位を利用した別解
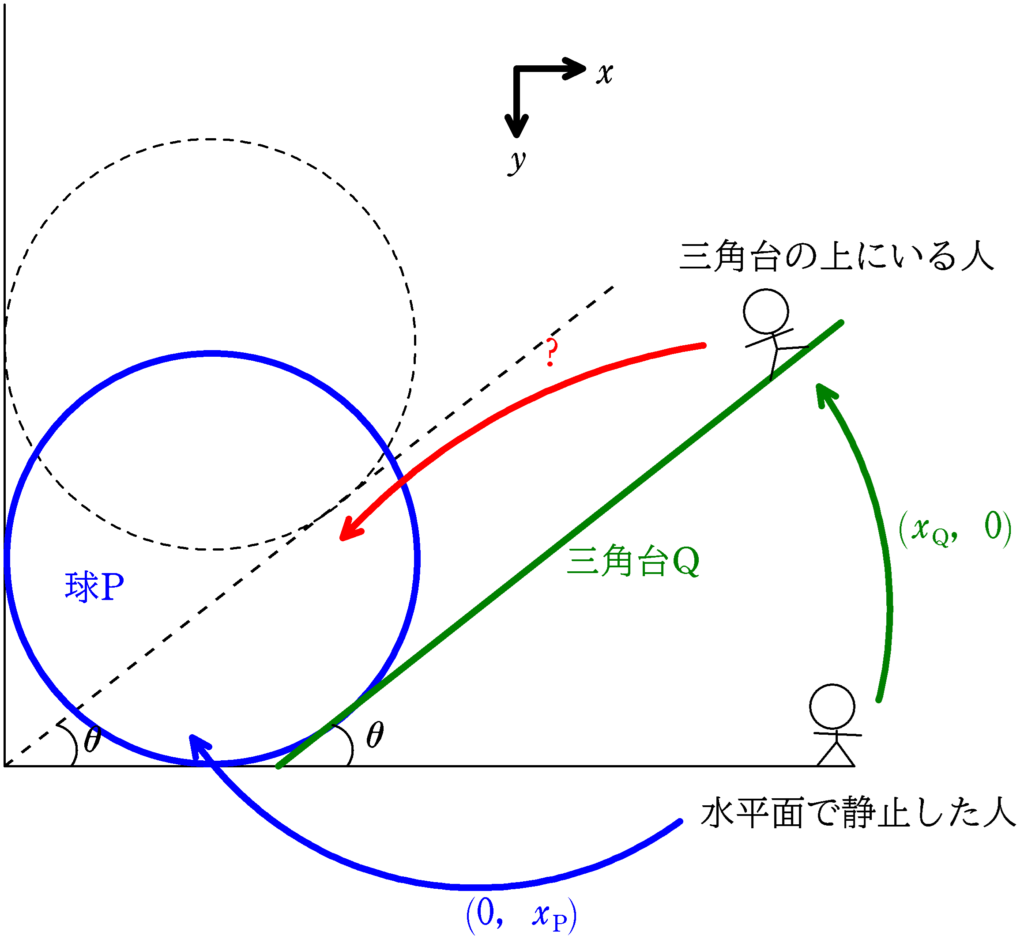
相対変位を利用して解くともう少し見通しがよくなります.
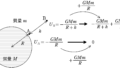
上図のように変位を設定します.つまり,水平面で静止した人からみた三角台Qの変位が$(x_{\rm Q},0)$($x$方向,$y$方向の向きは上図の通り),球Pの変位は$(0,x_{\rm P})$です.($y$方向に運動しているのに$x_{\rm P}$と書いてしまいました.紛らわしいという人は$y_{\rm P}$としてください.)
三角台からみた球Pの変位を$「?」$とすると次の関係が成り立ちます.
$(0,x_{\rm P})=(x_{\rm Q},0)+?$ $\cdots (\ast)$
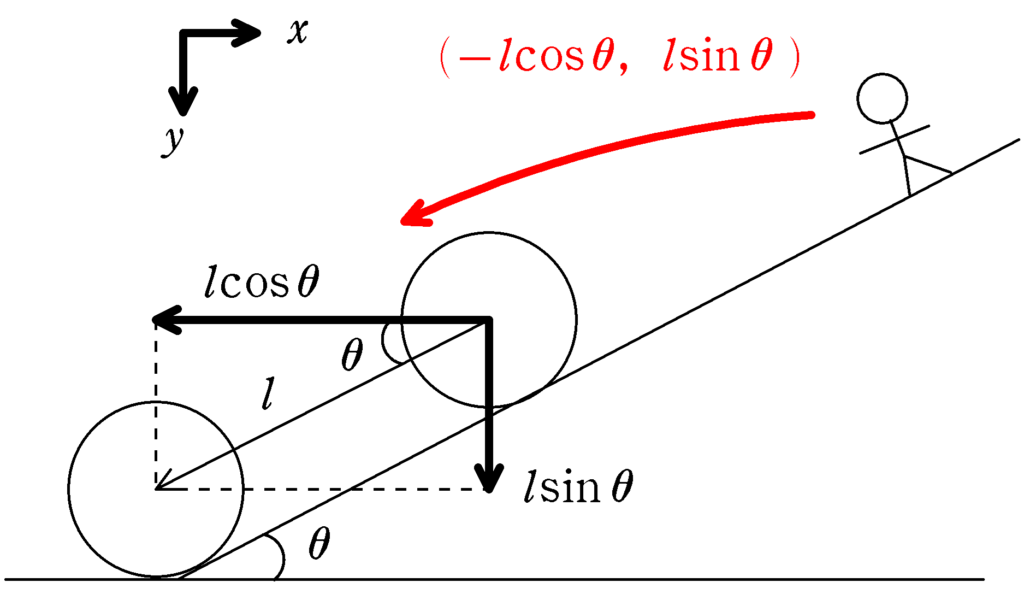
三角台Qからみると,球Pは斜面上を離れずすべっているので(束縛条件),移動距離を$l$として$x$方向,$y$方向に分解すると
$?=(-l\cos\theta,l\sin\theta)$
となります.これを$(\ast)$に代入すると
$(0,x_{\rm P})=(x_{\rm Q},0)+(-l\cos\theta,l\sin\theta)$
つまり,
$0=x_{\rm Q}-l\cos\theta$ かつ $x_{\rm P}=l\sin\theta$
であり,この2式から$l$を消去すれば
$x_{\rm P}=x_{\rm Q}\tan\theta$
を得て,さきほどの解法で出たものと同じ式がでてきます.
図2の方も同じ方法で解けるか確認してみましょう.
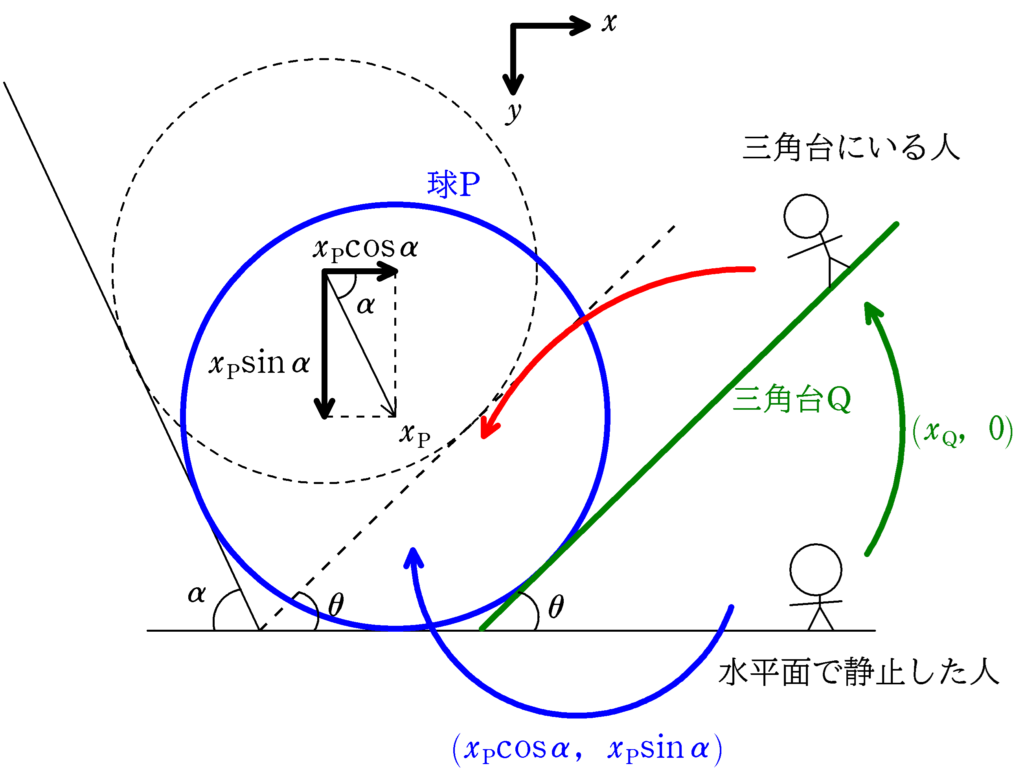
水平面で静止した人からみた三角台Qの変位が$(x_{\rm Q},0)$で図1の場合と同じです.球Pの変位を$x_{\rm P}$とし,これを$x$方向と$y$方向に分解すると
$(x_{\rm P}\cos\alpha,x_{\rm P}\sin\alpha)$
となります.
三角台からみた球Pの変位を$「?」$とすると次の関係が成り立ちます.
$(x_{\rm P}\cos\alpha,x_{\rm P}\sin\alpha)=(x_{\rm Q},0)+?$ $\cdots (2\ast)$

図1の場合と同様にして,三角台Qからみると,球Pは斜面上を離れずすべっているので(束縛条件),移動距離を$l$として$x$方向,$y$方向に分解すると
$?=(-l\cos\theta,l\sin\theta)$
となります.これを$(2\ast)$に代入すると
$(x_{\rm P}\cos\alpha,x_{\rm P}\sin\alpha)=(x_{\rm Q},0)+(-l\cos\theta,l\sin\theta)$
したがって
$x_{\rm P}\cos\alpha=x_{\rm Q}-l\cos\theta$ $\cdots (3\ast)$
かつ
$x_{\rm P}\sin\alpha=l\sin\theta$ $\cdots (4\ast)$
$(4\ast)$より,$l=\dfrac{x_{\rm P}\sin\alpha}{\sin\theta}$として,$(3\ast)$に代入します.
\begin{align} &x_{\rm P}\cos\alpha=x_{\rm Q}-\dfrac{x_{\rm P}\sin\alpha}{\sin\theta}\times \cos\theta \\ &\therefore\,\,\left(\cos\alpha+\dfrac{\sin\alpha}{\sin\theta}\right)x_{\rm P}=x_{\rm Q}\\ &\therefore\,\,\dfrac{\overbrace{\sin\theta\cos\alpha+\cos\theta\sin\alpha}^{加法定理でまとめる}}{\sin\theta}x_{\rm P}=x_{\rm Q}\\ &\therefore\,\, \dfrac{\sin(\theta+\alpha)}{\sin\theta}x_{\rm P}=x_{\rm Q}\\ &\therefore\,\, x_{\rm P}=\dfrac{\sin\theta}{\sin(\theta+\alpha)}x_{\rm Q} \end{align}
こちらも同じ形になりました.


コメント