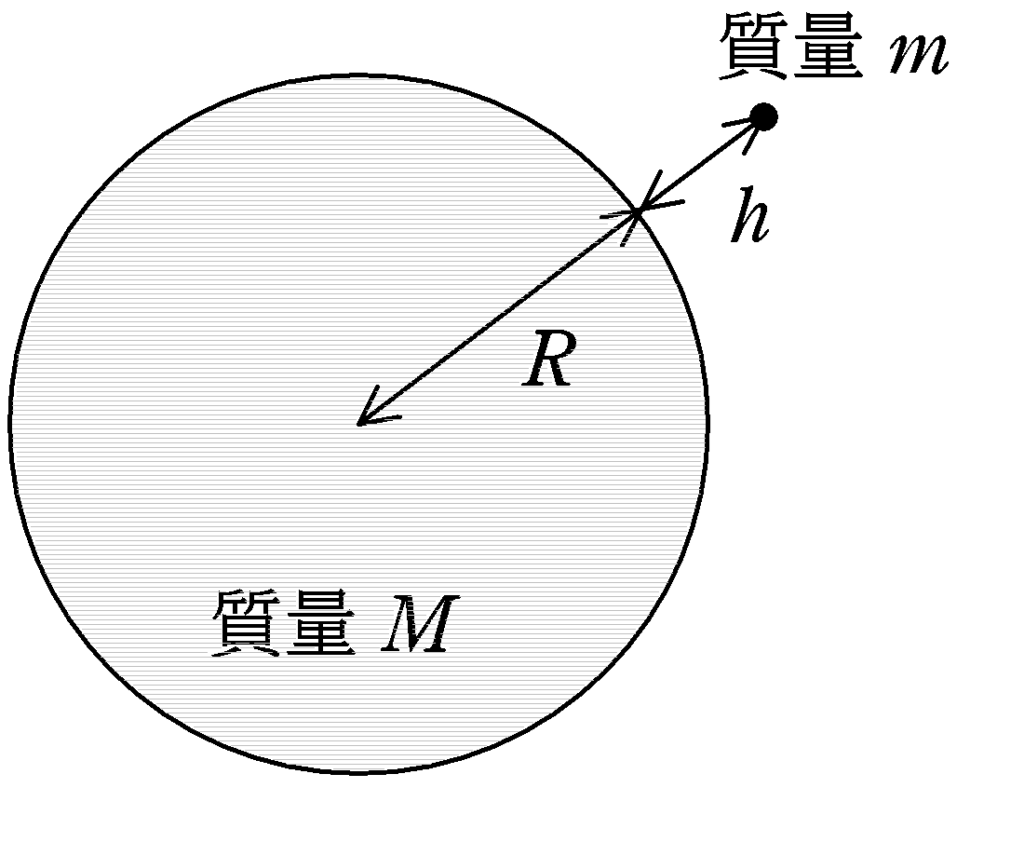
地球の質量を$M$,半径を$R$として,質量$m$の物体を地球表面より高さ$h$の場所にもっていくと,地球表面を基準点として,重力による位置エネルギー$U_{1}$は
$U_{1}=mgh$
になることはよく知られた式だと思います.
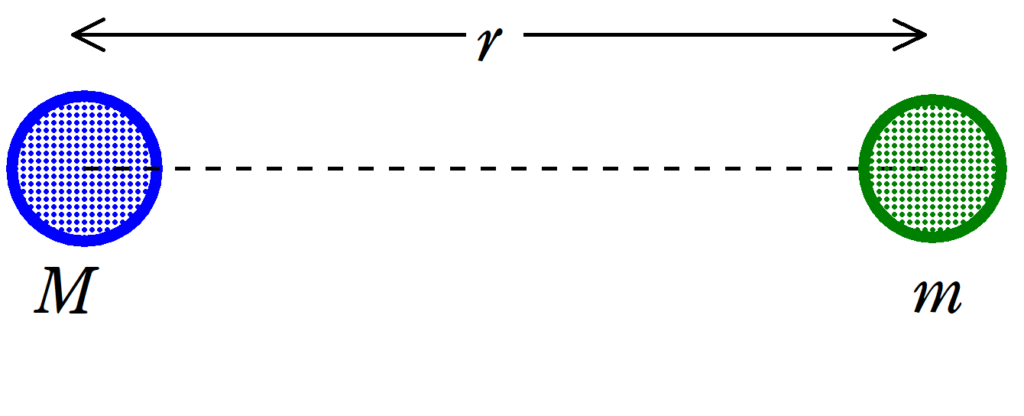
質量$M$と質量$m$の物体の距離を$r$とする.万有引力の位置エネルギーの基準点を無限遠とし,万有引力定数を$G$とすると,万有引力のよる位置エネルギー$U$は
$U=-G\dfrac{Mm}{r}$
一方,無限遠方を基準とした万有引力による位置エネルギー$U_{2}$は
$U_{2}=-\dfrac{GMm}{R}$
となります.$U_{1}$と$U_{2}$はなぜこんなにも違うのかを説明したいと思います.
そもそも位置エネルギーの基準点が違う.
そもそも$U_{1}$の基準点は地球表面で,$U_{2}$は無限遠方です.まずは,基準点を合わせるところからはじめましょう.
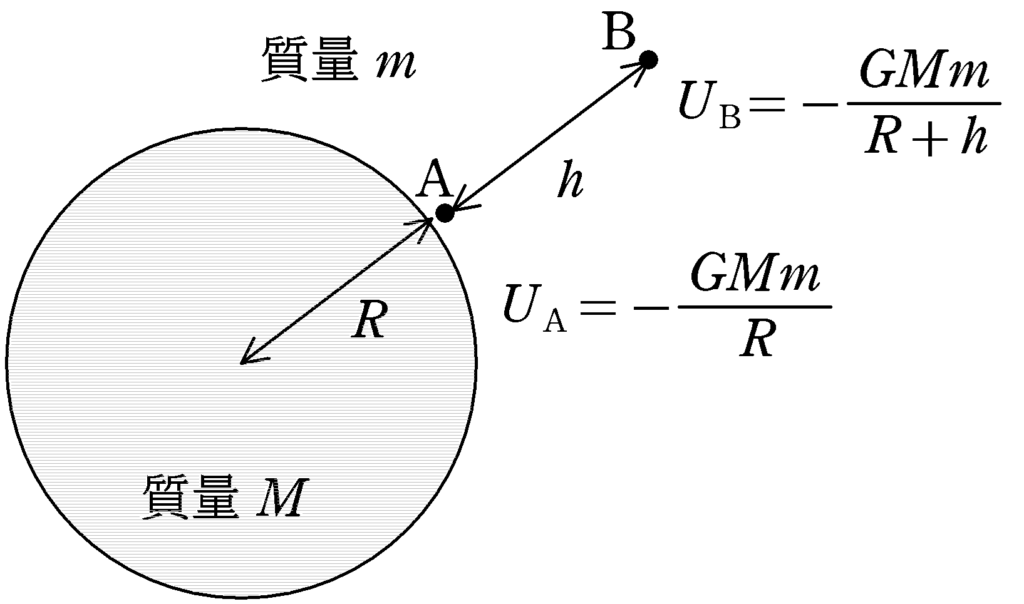
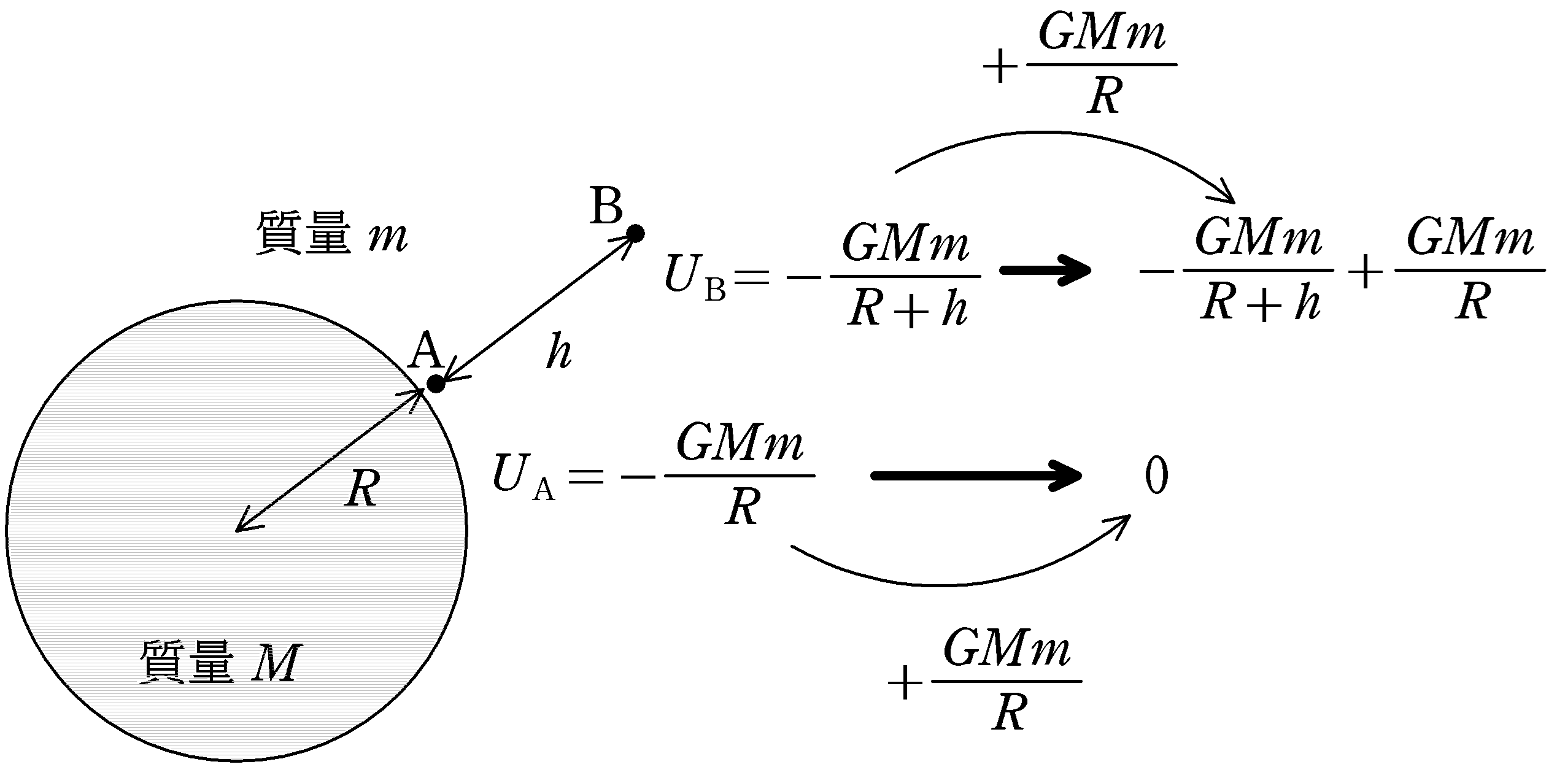
上図は地表表面をA点,A点より高さ$h$の点をB点としました.無限遠方を基準点としたA点とB点における万有引力による位置エネルギー$U_{\rm A},U_{\rm B}$は
$U_{\rm A}=-\dfrac{GMm}{R}$, $U_{\rm B}=-\dfrac{GMm}{R+h}$
となります.
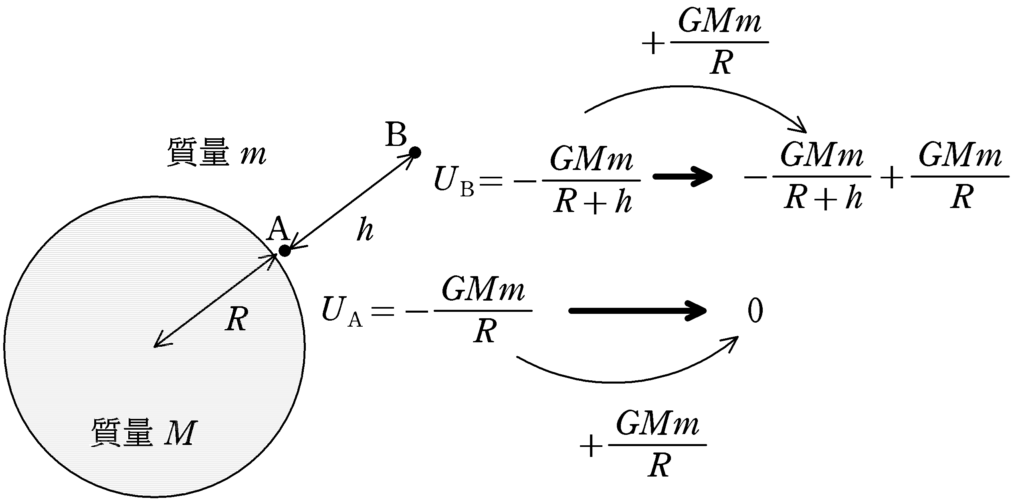
A点を基準点(つまり位置エネルギーを$0$)としたいと思います.$U_{\rm A}=-\dfrac{GMm}{R}$を$0$にするには,$\dfrac{GMm}{R}$を足せばよいので,同じくB点での位置エネルギーにも$-\dfrac{GMm}{R}$を足します.すると,A点(地表)を基準点としたB点での位置エネルギー$U_{\rm B}’$が計算できます.
\begin{align} U_{\rm B}’&=-\dfrac{GMm}{R+h}+\dfrac{GMm}{R}\\ &=GMm\left(\dfrac{1}{R}-\dfrac{1}{R+h}\right) \end{align}
重力加速度$g$と万有引力定数$G$の関係を使う.
半径$R$で質量$M$の惑星の表面上の重力加速度の大きさを$g$とする.
惑星の自転の影響を無視するとき,重力加速度の大きさ$g$と万有引力定数$G$には次の関係がある.
$gR^{2}=GM$
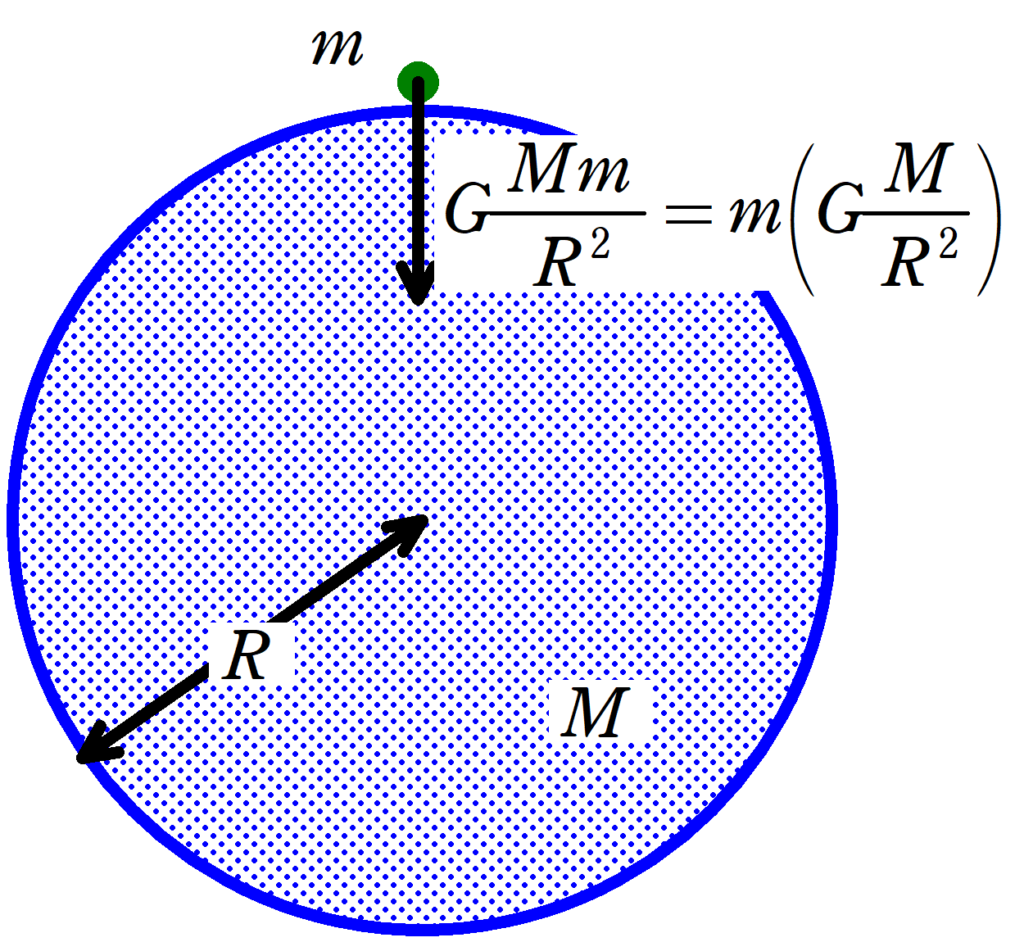
理由:上図より,$G\dfrac{Mm}{R^{2}}=mg$から,$gR^{2}=GM$
$GM=gR^{2}$を使って,$U_{\rm B}’$を変形しましょう.
\begin{align} U_{\rm B}’&=GMm\left(\dfrac{1}{R}-\dfrac{1}{R+h}\right)\\ &=gR^{2}\times m\left(\dfrac{1}{R}-\dfrac{1}{R+h}\right)\\ &=mgR^{2}\left(\dfrac{1}{R}-\dfrac{1}{R+h}\right) \end{align}
さらに括弧に中の$\dfrac{1}{R}$も外に無理やり出します.
$U_{\rm B}’=mgR\left(1-\dfrac{1}{1+\dfrac{h}{R}}\right)$
近似計算をつかう.
$R$が$h$に比べて十分小さいときを考えましょう.
$|\alpha|<<1$のとき
$(1+\alpha)^{n}\fallingdotseq 1+n\alpha$
$\dfrac{1}{1+\dfrac{h}{R}}$について
\begin{align} \dfrac{1}{1+\dfrac{h}{R}}&=\left(1+\dfrac{h}{R}\right)^{-1}\\ &\fallingdotseq 1-\dfrac{h}{R} \end{align}
より
\begin{align} U_{\rm B}’&=mgR\left(1-\dfrac{1}{1+\dfrac{h}{R}}\right)\\ &\fallingdotseq mgR\left\{1-\left(1-\dfrac{h}{R}\right)\right\}\\ &=mgR\times \dfrac{h}{R}\\ &=mgh=U_{1} \end{align}
ということで,確かに$U_{1}=U_{2}$となりました.$h$が$R$に対して小さい値でないと重力による位置エネルギー$U=mgh$の式も使えないことも理解ができたのではないかと思います.


コメント