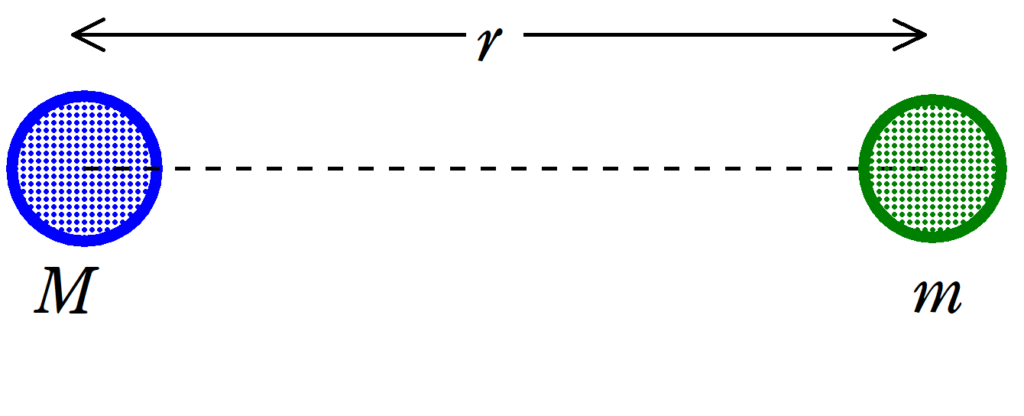
質量$M$と質量$m$の物体の距離を$r$とする.万有引力の位置エネルギーの基準点を無限遠とし,万有引力定数を$G$とすると,万有引力のよる位置エネルギー$U$は
$U=-G\dfrac{Mm}{r}$
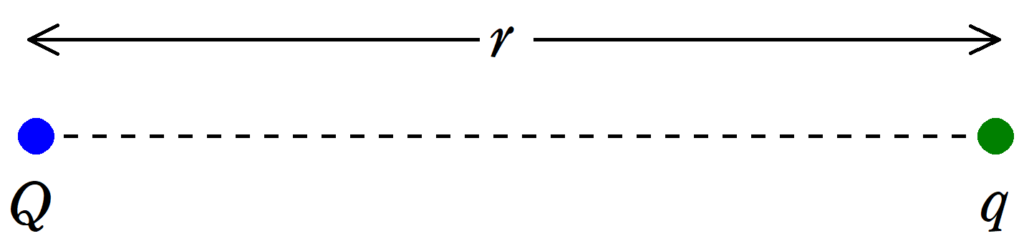
電荷$Q$と電荷$q$の点電荷どうしの距離を$r$とする.静電気力による位置エネルギーの基準点を無限遠とし,クーロンの比例定数を$k_{0}$とすると,静電気力による位置エネルギー$U$は
$U=k\dfrac{Qq}{r}$
※ 電荷の絶対値をとらないで計算すること.

なんで万有引力による位置エネルギーには「-」がついて,静電気力による位置エネルギーは「-」がついていないんだろう??

結論をいうと,
「万有引力は正の質量同士で引力がはたらく」
のに対して
「静電気力は同符号の電荷同士で斥力がはたらく」
ように決められたからです.
実際,静電気力による位置エネルギーは符号つきで計算します.
たとえば,$q_{1}(>0)$,$q_{2}>0$としたとき,次の3つの場合の位置エネルギーを考えてみましょう.
★ $Q=q_{1}$,$q=q_{2}$のとき (正電荷同士)
このときは斥力がはたらき,距離が$r$のときの位置エネルギー$U$は
$U=k_{0}\dfrac{q_{1}q_{2}}{r}$
★ $Q=q_{1}$,$q=-q_{2}$のとき (正電荷と負電荷)
このとき引力がはたらき,距離が$r$のときの位置エネルギー$U$は
$U=k_{0}\dfrac{q_{1}(-q_{2})}{r}=-k_{0}\dfrac{q_{1}q_{2}}{r}$
★ $Q=-q_{1}$,$q=-q_{2}$のとき (負電荷同士)
このとき斥力がはたらき,距離が$r$のときの位置エネルギー$U$は
$U=k_{0}\dfrac{(-q_{1})(-q_{2})}{r}=k_{0}\dfrac{q_{1}q_{2}}{r}$

確かに引力がはたらくときは位置エネルギーが「-」になっていて,斥力がはたらくときは位置エネルギーが「+」になるんだね.



コメント