[数学Ⅲ]物理の問題１ | Physicmath（フィジクマス）

問題

時刻$0 \rm s$において，水上$h[\rm m]$の高さの岸壁の上から$l_{0}[\rm m]$の網で引っ張られている船がある．いま，$V[\rm m/s]$の一定速度で網を引いて船を岸に引き寄せると，時刻$t[\rm s]$の船の速さを求めよ．

NEKO

数学Ⅲの物理の問題は微分，積分を積極的に使います．

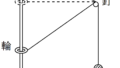
船の速さを計算するために，船の座標を下図のように岸を原点として水平方向に$x$座標を設定しましょう．

NEKO

網を一定の速さ$V$で引っ張るので，$t[\rm s]$後は網の長さが$l_{0}-Vt$となっています．

すると三平方の定理より

$x^{2}+h^{2}=(l_{0}-Vt)^{2}$

$\therefore$　$x=\sqrt{(l_{0}-Vt)^{2}-h^{2}}$

NEKO

座標$x$を時刻$t$で微分したものが速度$v$です．

$\eqalign{v&=\dfrac{dx}{dt}\\&=(l_{0}-Vt)^{\prime}\cdot 2(V_{0}-Vt)\cdot \dfrac{1}{2}\cdot \dfrac{1}{\sqrt{(l_{0}-Vt)^{2}-h^{2}}}\\&=-\dfrac{V(l_{0}-Vt)}{\sqrt{(l_{0}-Vt)^{2}-h^{2}}}}$

NEKO

速さを聞かれているので，絶対値を取って，

$\dfrac{V(l_{0}-Vt)}{\sqrt{(l_{0}-Vt)^{2}-h^{2}}}$(答)

が求める速さです．