twitterの問題27の解答

<問題>

＜解答＞

半減期の式

時刻$t=0$における放射性元素の数を$N_{0}$とする．時刻$t$における放射性元素の数を$N(t)$とする．半減期（放射性元素の数が半分になるまでの時間）を$T$とすると，次の式が成り立つ．

$N(t)=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$

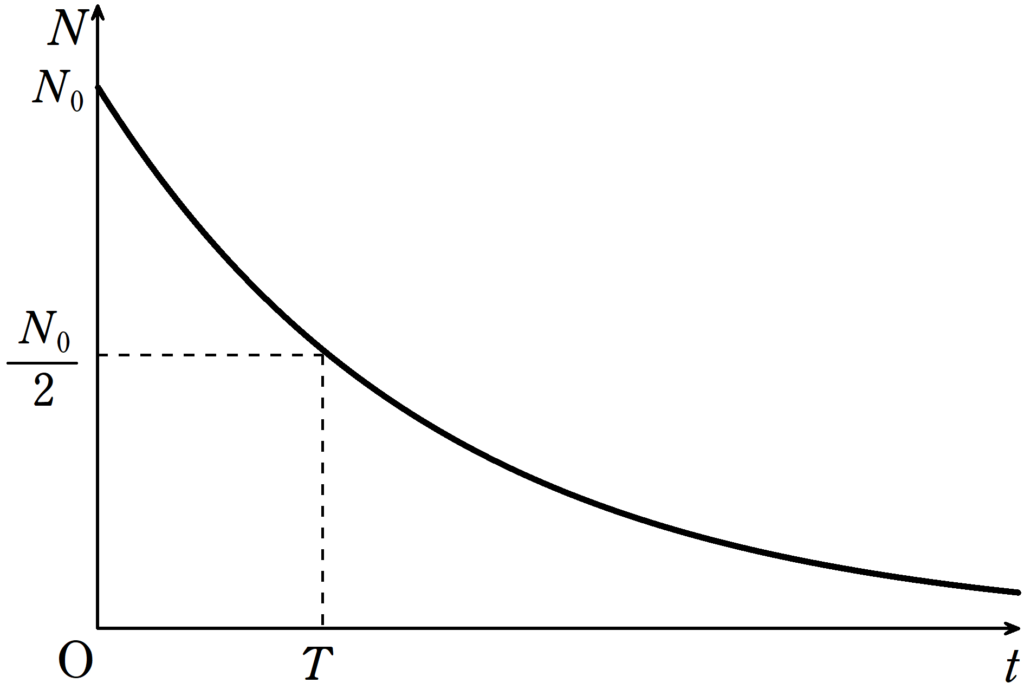
問題によれば，放射能の強さは$\dfrac{\varDelta N}{\varDelta t}$の絶対値をとったもものである．半減期の式より

$N=N_{0}\left(\dfrac{1}{2}\right)^{\frac{t}{T}}$　$\cdots (\ast)$

で，$T=4.0\times 10^{16}\,$秒で$\dfrac{t}{T}\ll 1$であるから，$\left(\dfrac{1}{2}\right)^{\frac{t}{T}}\fallingdotseq 1-0.69\cdot \dfrac{t}{T}$と近似できる．したがって，$(\ast)$は

$N$$=N_{0}\left(1-0.69\cdot \dfrac{t}{T}\right)=-\dfrac{0.69N_{0}}{T}$$t$$+N_{0}$

これは$y$$=a$$x$$+b$の形と同じ．$\dfrac{\varDelta y}{\varDelta x}=a$だから

$\dfrac{\varDelta N}{\varDelta t}=-\dfrac{0.69N_{0}}{T}　\cdots (2\ast)$

$(2\ast)$に$N_{0}=2.71\times 10^{20}$，$T=4.0\times 10^{16}$を代入して

$\dfrac{\varDelta N}{\varDelta t}=-\dfrac{0.69\times 2.71\times 10^{20}}{4.0\times 10^{16}}\fallingdotseq -4.7\times 10^{3}$

ちなみに放射能の強さの単位は$\rm Bq$（ベクレル）．答えは，$4.7\times 10^{3}\,[\rm Bq]$(答)