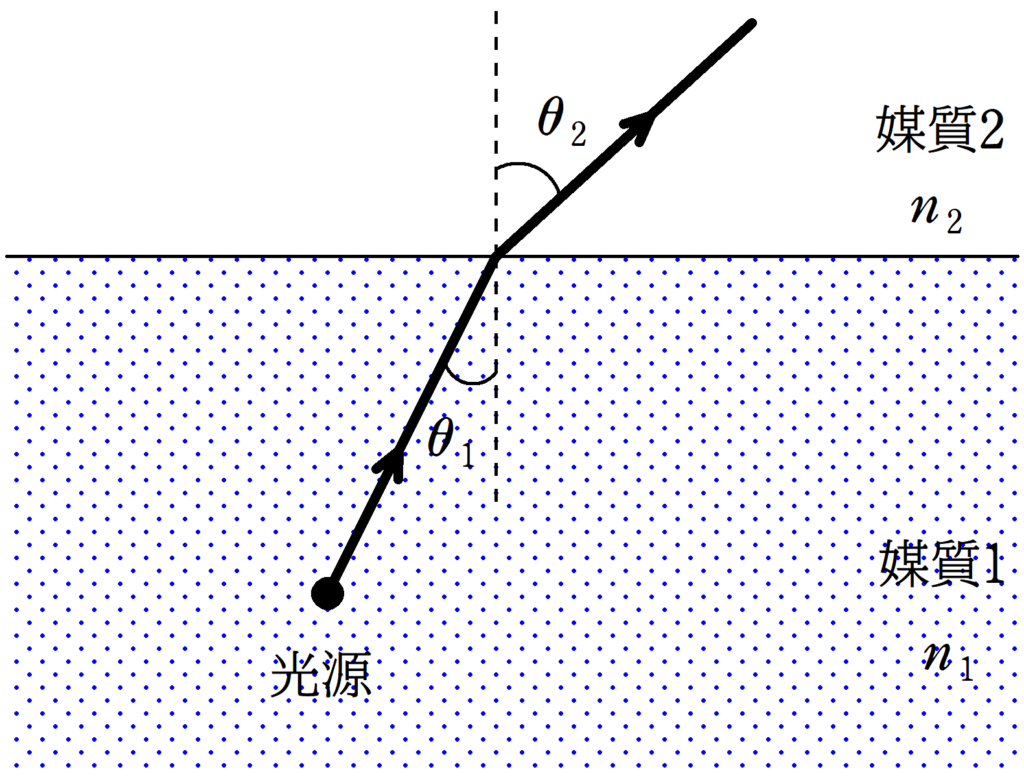
図のように,絶対屈折率$n_{1}$の媒質1と絶対屈折率$n_{2}$の媒質2がある.媒質1中に光源を固定して,光源から媒質2に向かって光を入射した.このときの入射角を$\theta_{1}$とする.次の問いに答えよ.
(1) 入射角$\theta_{1}$を$0^{\circ}$から少しずつ大きくしていった.すると,入射角が$\theta_{\rm C}$より大きくなると,光はすべて反射した.このとき,$\sin\theta_{\rm C}$を$n_{1}$,$n_{2}$を用いて表せ.
(2) (1)の$\theta_{\rm C}$が存在するための$n_{1}$,$n_{2}$の条件をかけ.
<解答>
(1)

屈折角が$90^{\circ}$のときの入射角を臨界角といいます.
屈折の法則を確認しましょう.
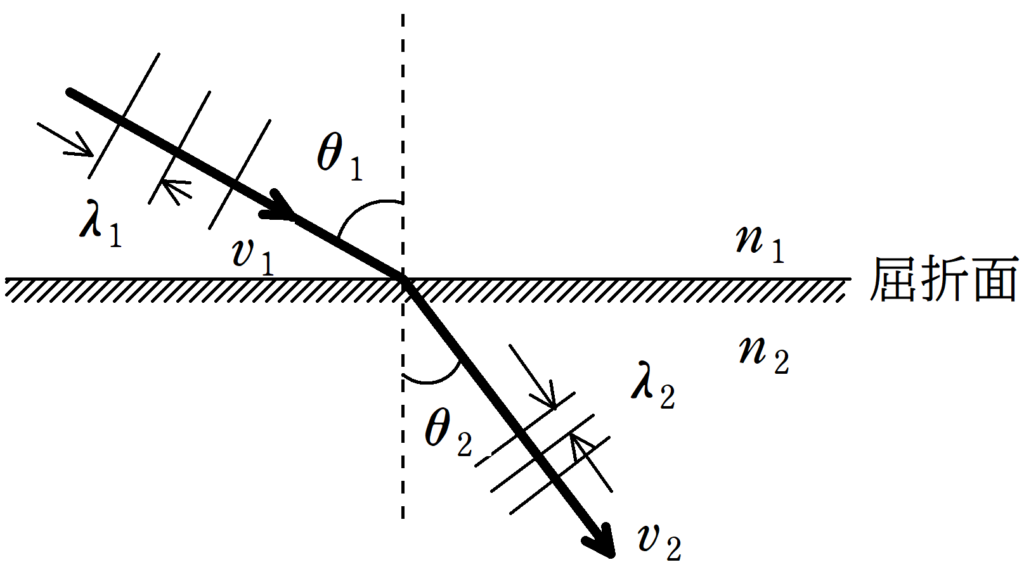
速さ$v_{1}$,波長$\lambda_{1}$の波が入射角$\theta_{1}$で屈折面に入射し,その後屈折角が$\theta_{2}$,速さ$v_{2}$,波長が$\lambda_{2}$となった.入射側の媒質の屈折率を$n_{1}$,屈折する側の媒質の屈折率を$n_{2}$とすると,次の関係が成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\sin\theta_{1}}{\sin\theta_{2}}$
また,屈折により,媒質の振動数$f$および周期$T$は変化しないことから,次のことが成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\cancel{f}\lambda_{1}}{\cancel{f}\lambda_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}$
一方,屈折率との関係は次のようになる.
$n_{1}\sin\theta_{1}=n_{2}\sin\theta_{2}$
$n_{1}v_{1}=n_{2}v_{2}$
$n_{1}\lambda_{1}=n_{2}\lambda_{2}$
最後に,$n_{12}=\dfrac{n_{2}}{n_{1}}$を屈折率$n_{1}$の媒質に対する屈折率$n_{2}$の媒質の相対屈折率という.
★ 屈折の法則
$n_{1}\sin\theta_{\rm C}=n_{2}\sin90^{\circ}$
$\sin\theta_{\rm C}=\dfrac{n_{2}}{n_{1}}$ (答)
(2)

臨界角よりもおおきな入射角で入射すると,屈折はせずすべて反射します.
これを全反射といいます.
しかし,全反射はどんな場合でも起こるわけではありません.
そもそも,臨界角が存在しないといけません.
(1)から,$\sin\theta_{\rm C}=\dfrac{n_{2}}{n_{1}}$より,$\theta_{\rm C}$が存在するための条件は
$\sin\theta_{\rm C}=\dfrac{n_{2}}{n_{1}}<1$

そもそも$\theta$が$0<\theta<90^{\circ}$のとき,$0<\sin\theta<1$となります.
したがって,臨界角が存在するには$n_{2}<n_{1}$(答)の条件が必要になります.
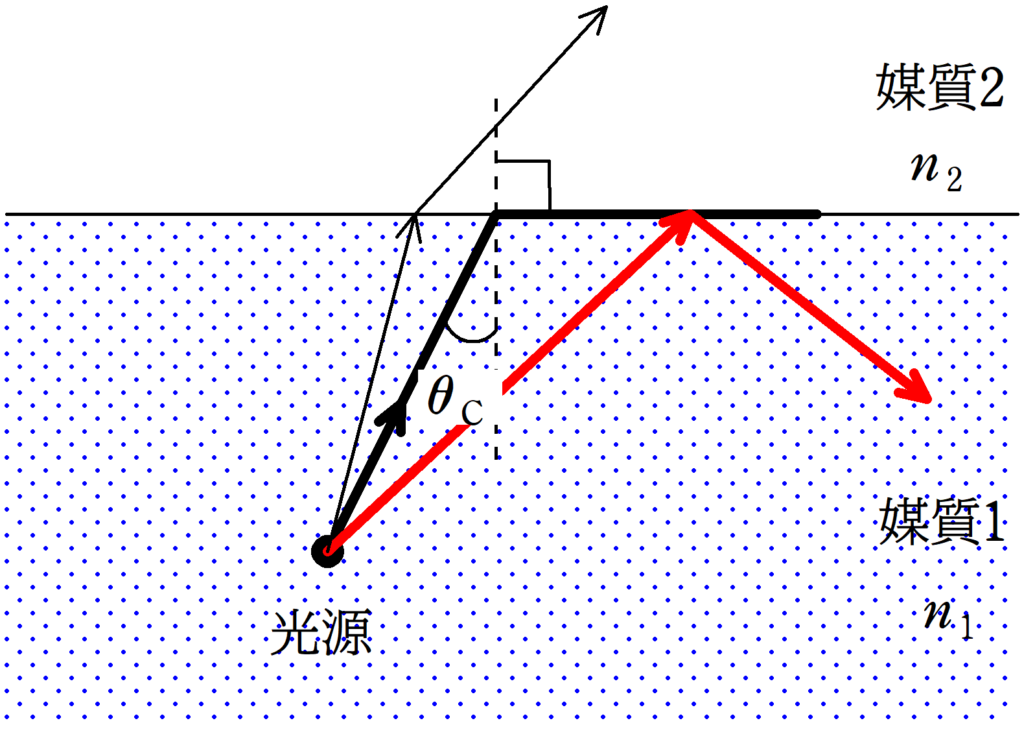
屈折角が$90^{\circ}$になるときの入射角を臨界角という.入射角が臨界角よりも大きいとき,全反射する.ただし,臨界角が存在するためには,入射側の媒質の屈折率の方が屈折側の媒質よりも大きい必要がある.(屈折率が同じ場合はそもそも反射しない.)
上図のような屈折率の媒質1,2を考えるとき,臨界角を$\theta_{\rm C}$として,屈折の法則より,
$n_{1}\sin\theta_{\rm C}=n_{2}\sin 90^{\circ}$
$\sin\theta_{\rm C}=\dfrac{n_{2}}{n_{1}}$
全反射する条件は,
$\theta_{\rm C}<入射角$
臨界角が存在する条件は
$n_{1}>n_{2}$
である.



コメント