twitterの解答59 中途半端な位相のずれがあるときの振幅0の位置

定常波の節の数を求める3つの問題．
この手の問題はどうやって解く方法が多いのだろうか．
1.図をかく，2.弱め合いの条件を考える，3.波の式から和積で合成 pic.twitter.com/KRCZZqfQnB
— フィジクマス (@physicmath2) March 5, 2023

＜問題＞

<解答>

上2つの問題は図をかけばすぐに解けますが，一番下の問題は図を描きにくいです．こういう問題のときは「弱め合いの条件」を考えるか，「波の式」を立てて和積の公式より式を変形し，振幅が$0$の位置を求める方法があります．今回は前者で考えていきたいと思います．

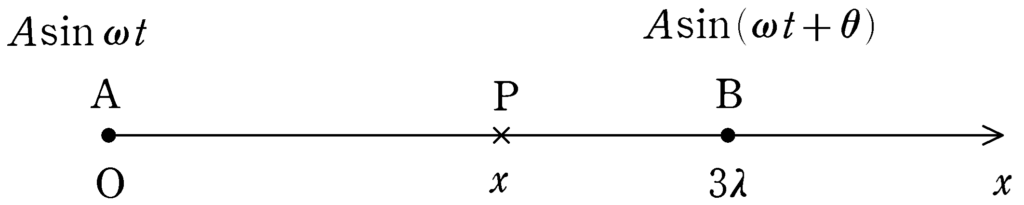
上のように，角振動数を$\omega$，振幅を$A$として，点Aでは$A\sin(\omega t)$，点Bでは$A\sin(\omega t+\theta)$で振動しているとしましょう．$\theta$が位相のずれです．Aを原点とし，Bの方向に$x$座標をとったとき，座標$x\,(0<x<3\lambda)$である点Pでの弱めい合いの条件を考えていきます．

たとえば，点Aが単振動すると点Aから距離$r$離れた位置では点Aの振動から少し遅れて振動が伝わります．（参考「[暗記するだけでは×]波の式を立てる」）$\sin$のなかの部分を「位相」といいますが，（参考「位相って何！？[高校物理]」）距離$r$離れた位置での位相の遅れ$\phi$は波長$\lambda$分で$2\pi$分ずれるので

$2\pi：\lambda=\phi：r$　$\therefore\,\, \phi=\dfrac{2\pi}{\lambda}r$

となります．AP間の距離が$x$なので位相の遅れが$\dfrac{2\pi}{\lambda}x$，BP間の距離が$3\lambda-x$なので位相の遅れが$\dfrac{2\pi}{\lambda}\times (3\lambda-x)$となります．

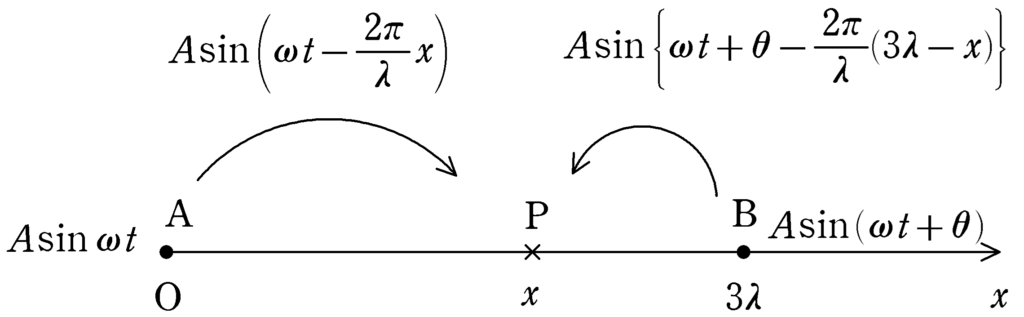
すると，点Aから出る波の点Pにおける位相$\phi_{\rm A}$は，

$\phi_{\rm A}=\omega t-\dfrac{2\pi}{\lambda}x$

点Bから出る波の点Pにおける位相$\phi_{\rm B}$は，

$\phi_{\rm B}=\omega t+\theta-\dfrac{2\pi}{\lambda}\times (3\lambda-x)$

したがって，点Pにおける位相差は

\begin{align} \phi_{\rm B}-\phi_{\rm A}&=\omega t+\theta-\dfrac{2\pi}{\lambda}\times (3\lambda-x)-\left(\omega t-\dfrac{2\pi}{\lambda}x\right)\\ &=\dfrac{2\pi}{\lambda}\times (2x-3\lambda)+\theta \end{align}

$m$を整数として，弱めい合いの条件は位相差が$2\pi m+\pi$のときであるから

$\dfrac{2\pi}{\lambda}\times (2x-3\lambda)+\theta=2\pi m+\pi$

$\therefore\,\, x=\dfrac{1}{2}\left(m+\dfrac{7}{2}-\dfrac{\theta}{2\pi}\right)\lambda$　$\cdots (\ast)$

この$x$が$0<x<3\lambda$を満たす条件より，($x=0，3\lambda$は外力を加えて振動させているので省く)

$0<\dfrac{1}{2}\left(m+\dfrac{7}{2}-\dfrac{\theta}{2\pi}\right)\lambda<3\lambda$

$\therefore\,\, \dfrac{\theta}{2\pi}-\dfrac{7}{2}<m<\dfrac{5}{2}+\dfrac{\theta}{2\pi}$　$\cdots (2\ast)$

★　位相のずれがない場合

$(2\ast)$に$\theta=0$を代入して

$-\dfrac{7}{2}<m<\dfrac{5}{2}$

この不等式を満たす$m$は，$m=-3，-2，-1，0，1，2$であり，計6個(答)の振幅が0の点がある．これらの$m$の値を$(\ast)$に代入すると，振幅が$0$の$x$座標がわかる．

★　逆位相の振動の場合

$(2\ast)$に$\theta=\pi$を代入して