
コンデンサーにかけることが電圧には限界があります.
これを耐電圧というんですが,ときどき入試問題にも出題されるので,演習をしておきましょう.
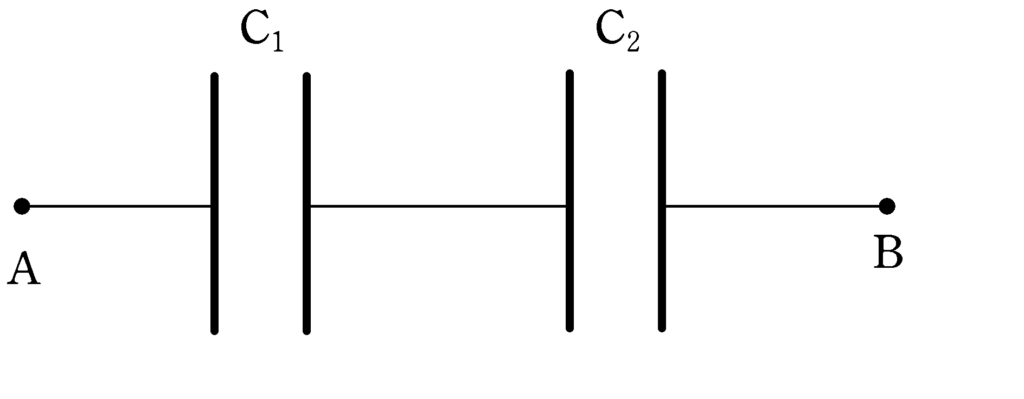
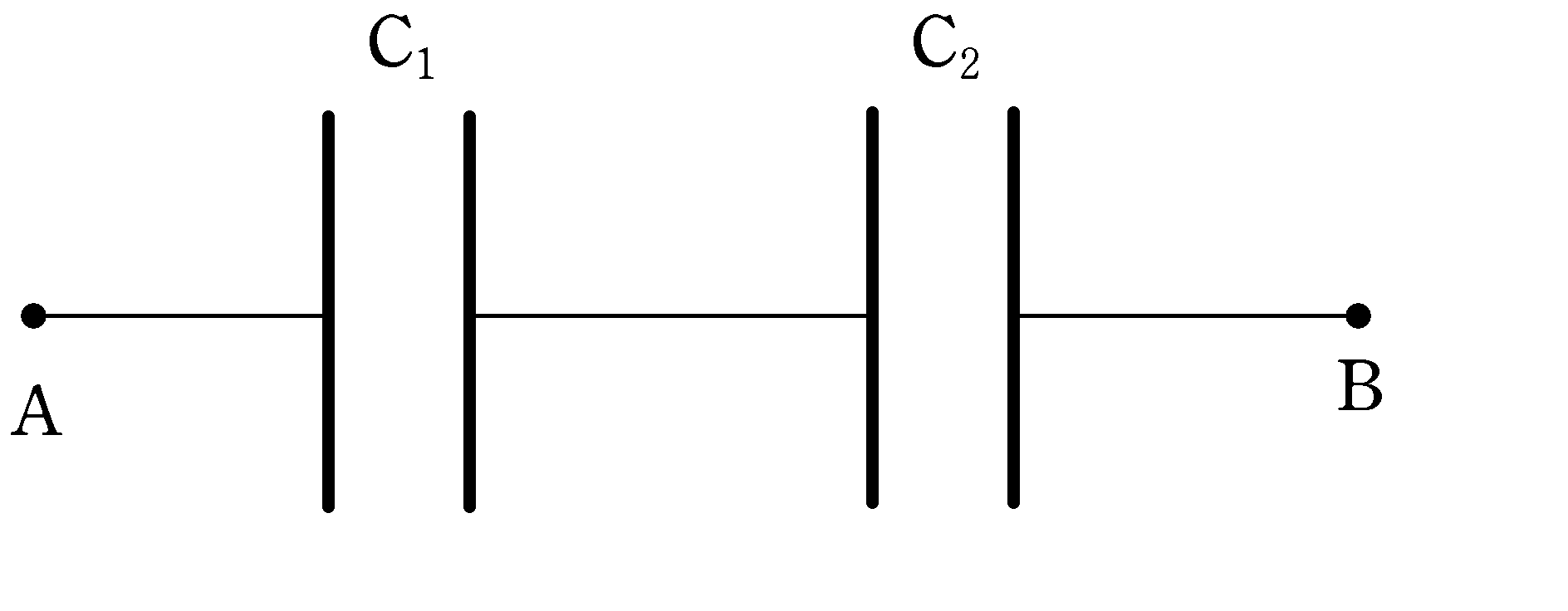
上図のように,帯電していない2つのコンデンサー$\rm C_{1} , C_{2}$がある.コンデンサーの電気容量と耐電圧が次の場合であるとき,ABにかけることができる最大電圧はいくらか.
(1) $\rm C_{1}$の電気容量は$C$,耐電圧が$3V$,$\rm C_{2}$の電気容量が$2C$,耐電圧が$2V$.
(2) $\rm C_{1}$の電気容量は$3C$,耐電圧が$3V$,$\rm C_{2}$の電気容量が$2C$,耐電圧が$2V$.

直列で電荷が蓄えられてないコンデンサーの場合の電気容量と電圧の比は次のようになります.
次のことは覚えていなくてもいいので,条件を入れて導けるようにしておくとよいです.
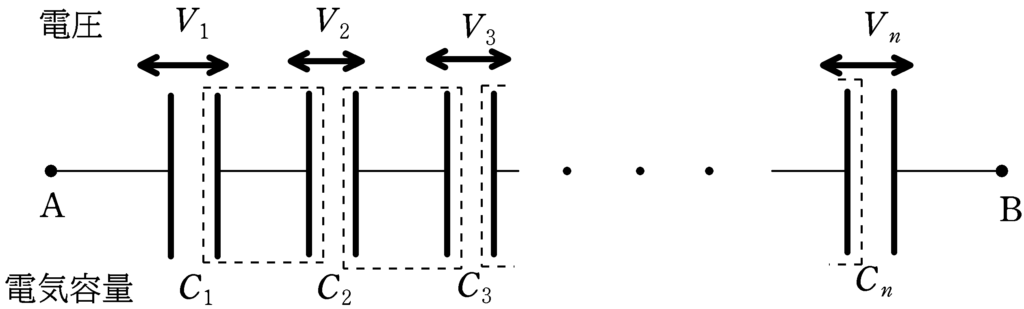
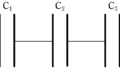
図のような電気容量$C_{1} , C_{2} , C_{3} , \cdots , C_{n}$の$n$個のコンデンサーがある.点線部分の電荷の和が0のとき,AB間に電圧をかけると,どのコンデンサーも蓄えられる電荷が同じなので,電気容量$C$と電圧$V$には
$CV=$一定 すなわち $V=\dfrac{定数}{C}$
の関係がある.つまり,
$V_{1}:V_{2}:\cdots :V_{n}=\dfrac{1}{C_{1}}:\dfrac{1}{C_{2}}:\cdots :\dfrac{1}{C_{n}}$
が成り立つ.
<解答>
(1)

電気容量$C , 2C$のコンデンサーにかかる電圧をそれぞれ$V_{1} , V_{2}$とすると,
$V_{1}:V_{2}=\dfrac{1}{C}:\dfrac{1}{2C}=2:1$
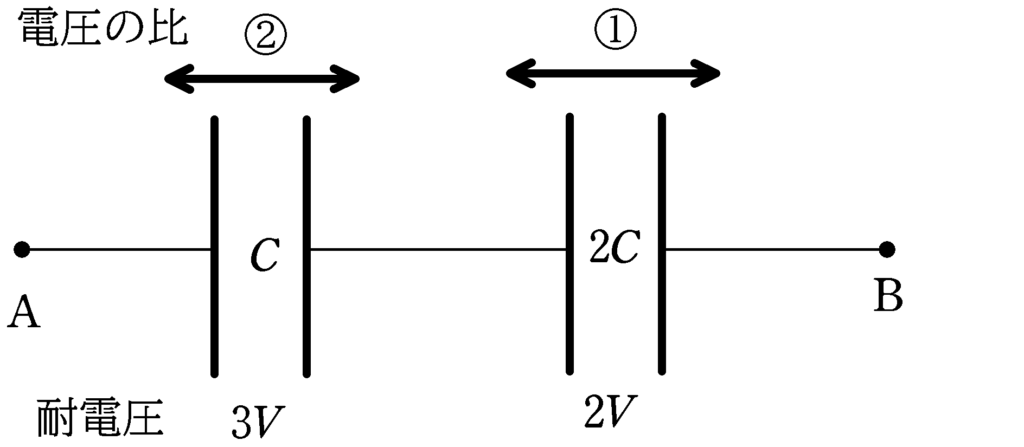

例えば,$2C$のコンデンサーにかかる電圧が耐電圧ギリギリの$2V$のとき,電圧の比から,$C$のコンデンサーにかかる電圧は$4V$になりますが,これは$C$のコンデンサーの耐電圧を超えるので不適です.
そこで,$C$の方のコンデンサーの耐電圧$3V$に合わせましょう.すると,電圧の比から$2C$の方向のコンデンサーにかかる電圧は$\dfrac{3}{2}V$となります.
したがって,AB間の電圧は
$3V+\dfrac{3}{2}V=\dfrac{9}{2}V$ (答)
(2)

電気容量$3C , 2C$のコンデンサーにかかる電圧をそれぞれ$V_{1} , V_{2}$とすると,
$V_{1}:V_{2}=\dfrac{1}{3C}:\dfrac{1}{2C}=2:3$
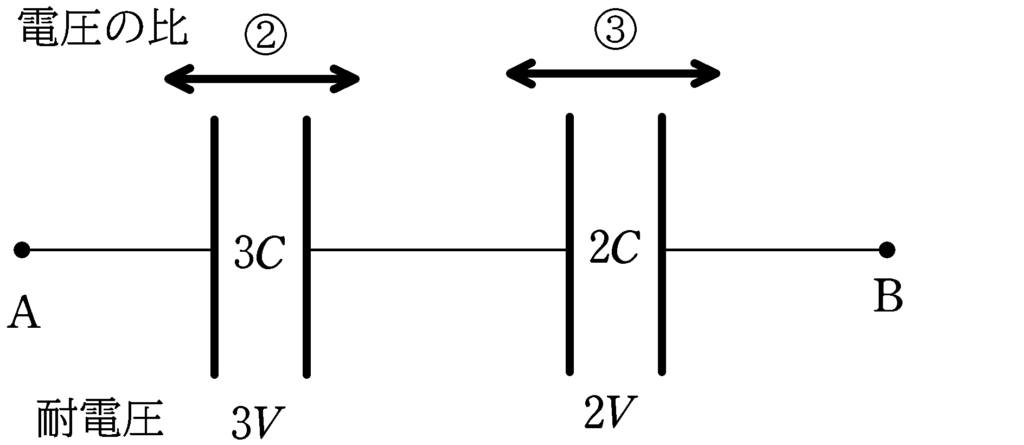

例えば,$3C$のコンデンサーにかかる電圧が耐電圧ギリギリの$3V$のとき,電圧の比から,$2C$のコンデンサーにかかる電圧は$3C\times \dfrac{3}{2}=\dfrac{9}{2}$になりますが,これは$2C$のコンデンサーの耐電圧を超えるので不適です.
そこで,$2C$の方のコンデンサーの耐電圧$2V$に合わせましょう.すると,電圧の比から$3C$の方向のコンデンサーにかかる電圧は$2V\times \dfrac{2}{3}=\dfrac{4}{3}V$となります.
したがって,AB間の電圧は
$\dfrac{4}{3}V+2V=\dfrac{10}{3}V$ (答)

コメント
[…] […]