
今回は楕円の周期$T$を面積速度$A$と楕円の面積$S$の関係から求めていきたいと思います.
周期$T$と面積速度$A$と楕円の面積$S$の関係
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\Delta S}{\Delta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.
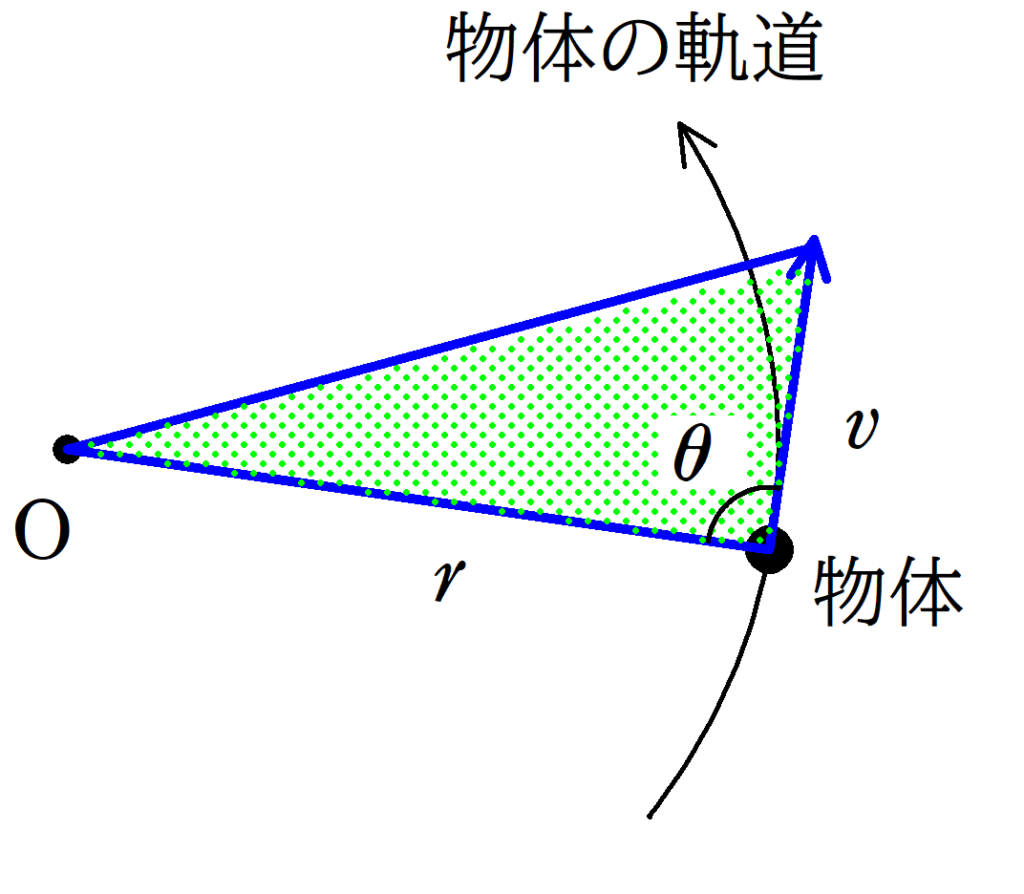
上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}rv\sin\theta$
面積速度$\times$微小時間$=$微小時間に通過した面積
より,
面積速度$\times $周期$=$1周して通過した面積の和
つまり
$A\times T=S$ $\therefore T=\dfrac{S}{A} \cdots (\ast)$
楕円の面積速度$A$を計算する
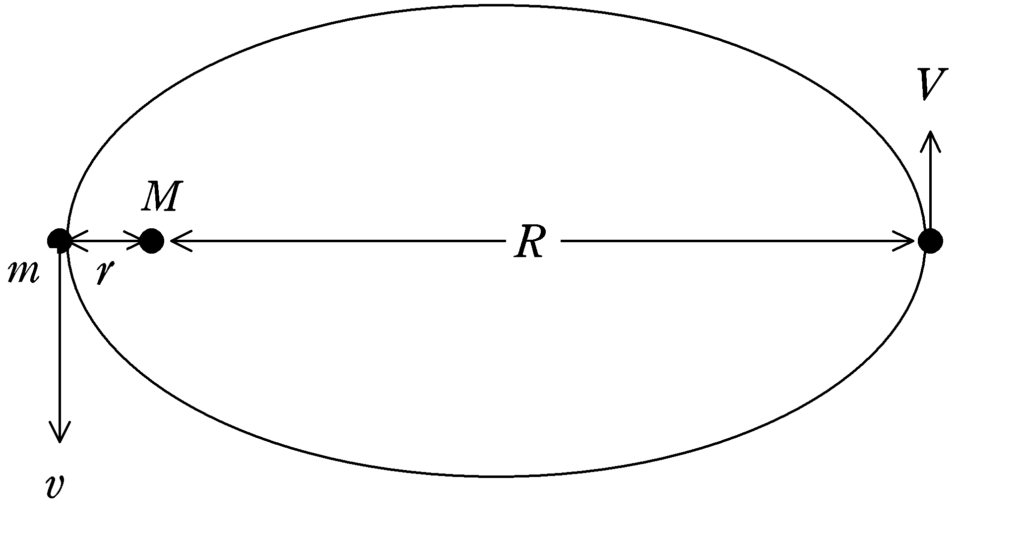

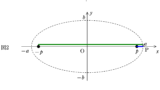
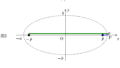
上図のように,質量$M$の天体Aのまわりを質量$m$の人工衛星Bが楕円運動しているときを考えます.
AとBが最も近づくときの距離を$r$,速さを$v$,最も遠ざかるときの距離が$R$,速さを$V$とします.
面積速度一定の法則と力学的エネルギー保存則を立てていきます.万有引力定数は$G$としてください.
★ 面積速度一定の法則
$\dfrac{1}{2}rv=\dfrac{1}{2}RV$ $\therefore V=\dfrac{r}{R}v$ $\cdots (2\ast)$
★ 力学的エネルギー保存則
$\dfrac{1}{2}\cancel{m}v^{2}-\dfrac{GM\cancel{m}}{r}=\dfrac{1}{2}\cancel{m}V^{2}-\dfrac{GM\cancel{m}}{R}$
$(2\ast)$を代入して$v$について求める.
$\dfrac{1}{2}v^{2}-\dfrac{GM}{r}=\dfrac{1}{2}\left(\dfrac{r}{R}v\right)^{2}-\dfrac{GM}{R}$
$\therefore\,\, \dfrac{1}{2}v^{2}\left(1-\dfrac{r^{2}}{R^{2}}\right)=\left(\dfrac{1}{r}-\dfrac{1}{R}\right)GM$
$\therefore\,\, \dfrac{1}{2}v^{2}\cdot \dfrac{(R+r)\cancel{(R-r)}}{R^{2}}=\dfrac{\cancel{(R-r)}GM}{Rr}$
$\therefore\,\, v=\sqrt{\dfrac{2RGM}{(R+r)r}}$
★ 面積速度
したがって,面積速度$A$は
$A=\dfrac{1}{2}rv=\dfrac{1}{2}r\sqrt{\dfrac{2RGM}{(R+r)r}}=\sqrt{\dfrac{RrGM}{2(R+r)}}$ $\cdots (3\ast)$
楕円の面積$S$を求める
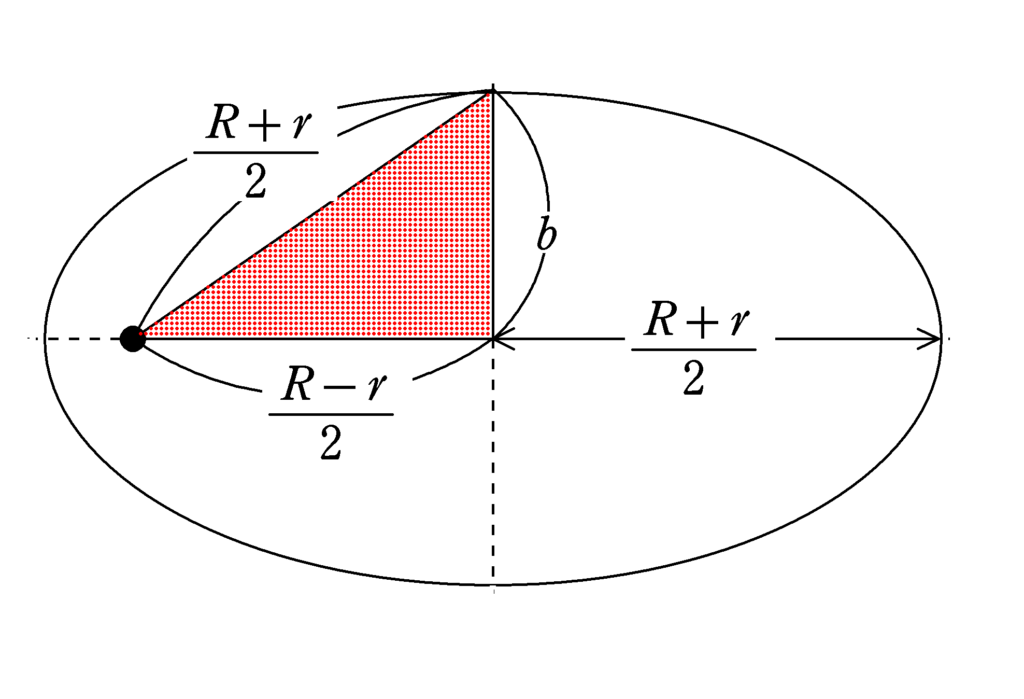

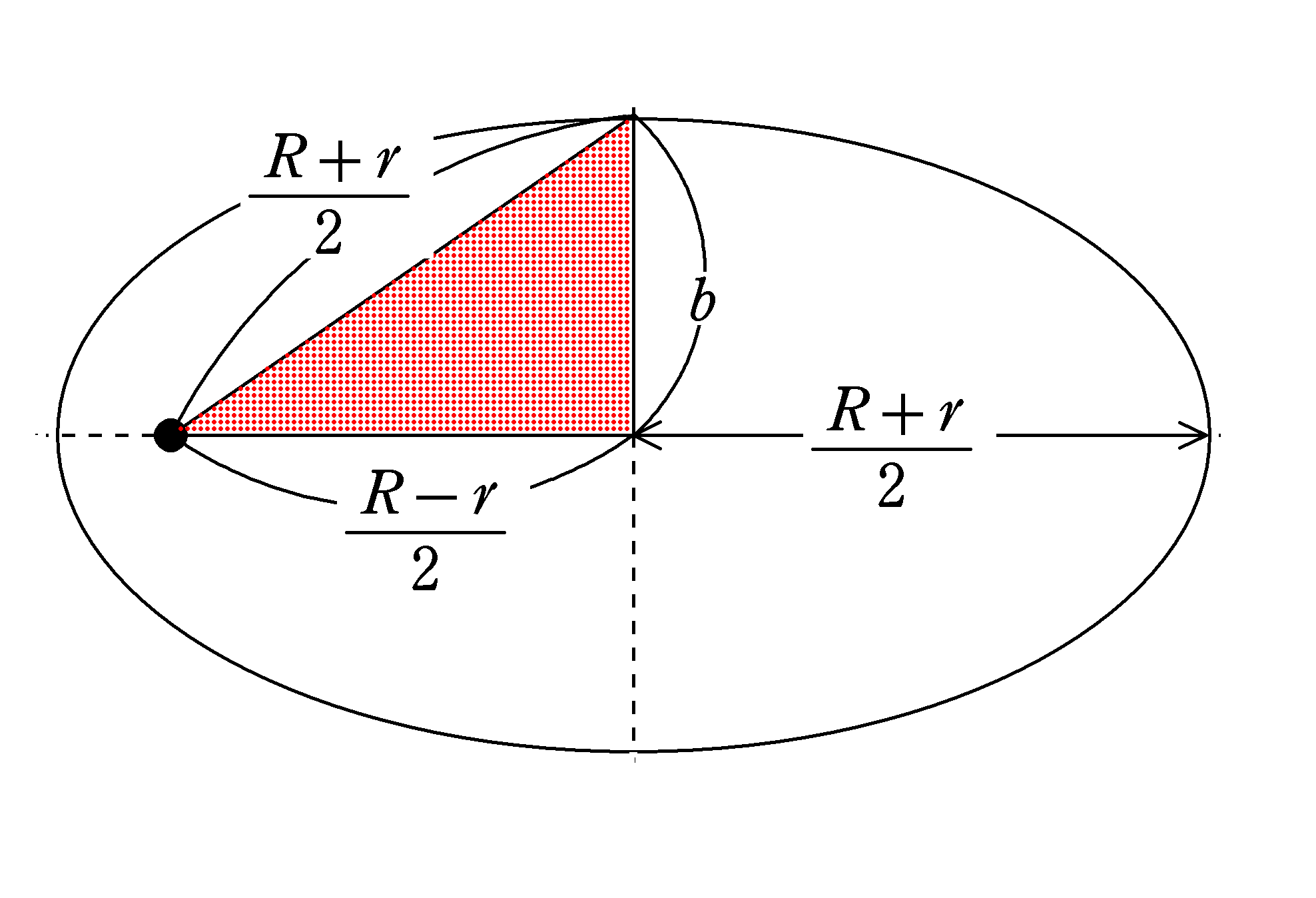
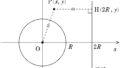
長軸の半径は$\dfrac{R+r}{2}$です.また,楕円の中心と焦点の距離は
$\dfrac{R+r}{2}-r=\dfrac{R-r}{2}$となります.
楕円の長軸半径と短軸半径と中心と焦点までの距離の関係より,短軸半径$r$を求めていきます.この関係については次の記事を参考にしてください.
★ 図の赤い部分の直角三角形について,三平方の定理より
$b^{2}+\left(\dfrac{R-r}{2}\right)^{2}=\left(\dfrac{R+r}{2}\right)^{2}$
$\therefore b=\sqrt{Rr}$
★ 楕円の面積
楕円の面積$S$は
$S=\pi\times \dfrac{R+r}{2}\times \sqrt{Rr}=\dfrac{\pi(R+r)\sqrt{Rr}}{2}$ $\cdots (4\ast)$
楕円の周期を$T$を求める
$T=\dfrac{S}{A} \cdots (\ast)$,$A=\sqrt{\dfrac{RrGM}{2(R+r)}} \cdots (3\ast)$,$S=\dfrac{\pi(R+r)\sqrt{Rr}}{2}$ $\cdots (4\ast)$より
$T=\dfrac{S}{A}=\dfrac{\pi(R+r)\sqrt{Rr}}{2}\times \sqrt{\dfrac{2(R+r)}{RrGM}}=\pi(R+r)\sqrt{\dfrac{R+r}{2GM}}$

これで楕円の周期を求めることができました.
最後にケプラーの第3法則で解く方法と一致するかどうか調べてみましょう.
ケプラーの第3法則を用いた方法
半径$r$の等速円運動をしている際の向心方向の運動方程式は,速さを$v_{0}$として
$m\dfrac{v_{0}^{2}}{r}=\dfrac{GMm}{r^{2}}$ $\therefore\,\,v_{0}=\sqrt{\dfrac{GM}{r}}$
半径$r$の等速円運動の周期$T_{0}$は
$T_{0}=\dfrac{2\pi r}{v_{0}}=2\pi r\sqrt{\dfrac{r}{GM}}$
ケプラーの第3法則より,周期の2乗は長軸の半径の3乗に比例するので
$T_{0}^{2}:T^{2}=r^{3}:\left(\dfrac{R+r}{2}\right)^{3}$
$\eqalign{T^{2}&=\dfrac{\dfrac{(R+r)^{3}}{8}}{r^{3}}\cdot T_{0}^{2}\\&=\dfrac{(R+r)^{3}}{8\cancel{r^{3}}}\cdot \dfrac{4\pi^{2}\cancel{r^{3}}}{GM}=\dfrac{\pi^{2}(R+r)^{3}}{2GM}}$
したがって,$T=\pi(R+r)\sqrt{\dfrac{R+r}{2GM}}$

結果は一致しました.

コメント