
PHYさん
楕円の知識は時々万有引力を絡めた問題で必要になるので確認しておきます.
とりあえず,高校物理では次のことを押さえておくとよいでしょう.
楕円についておさえておくこと
- 楕円は2焦点からの距離の和が一定の軌跡
- 楕円の方程式は正の定数$a,b$を用いて次のように表され,このとき,長軸と短軸の半径は$a,b$である.($a,b$のうち大きい方が長軸の半径)
$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$
- 楕円の面積は$\pi ab$

PHYさん
さらに,数学IIIでも習った通り次のことをも言えます.
楕円についておさえておくこと2
楕円の方程式が$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$$\,\,(a>b>0)$であるとき,
- 2焦点からの距離の和は$2a$である.
- 楕円の中心と焦点の距離を$p$とすると,$p^{2}+b^{2}=a^{2}$が成り立つ.

PHYさん
上のことを確かめておきましょう.
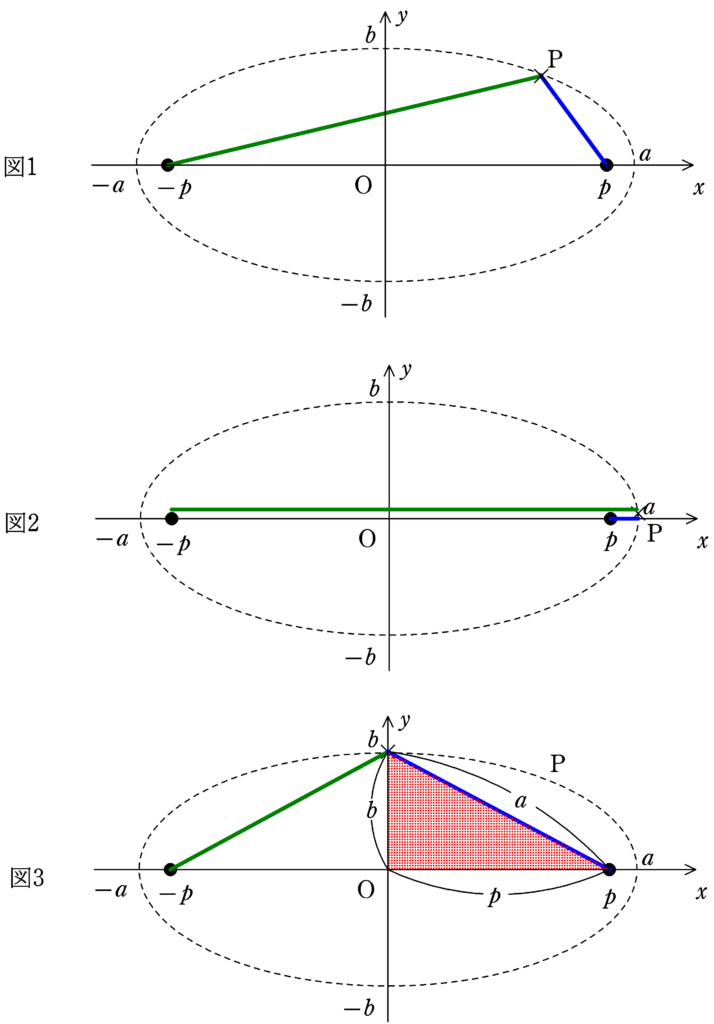
まず,下図1のように楕円の中心を
原点とし,焦点の座標を$(p,0)$,$(-p,0)$とします.
楕円は緑の線と青の線の長さの和が一定の軌跡です.

PHYさん
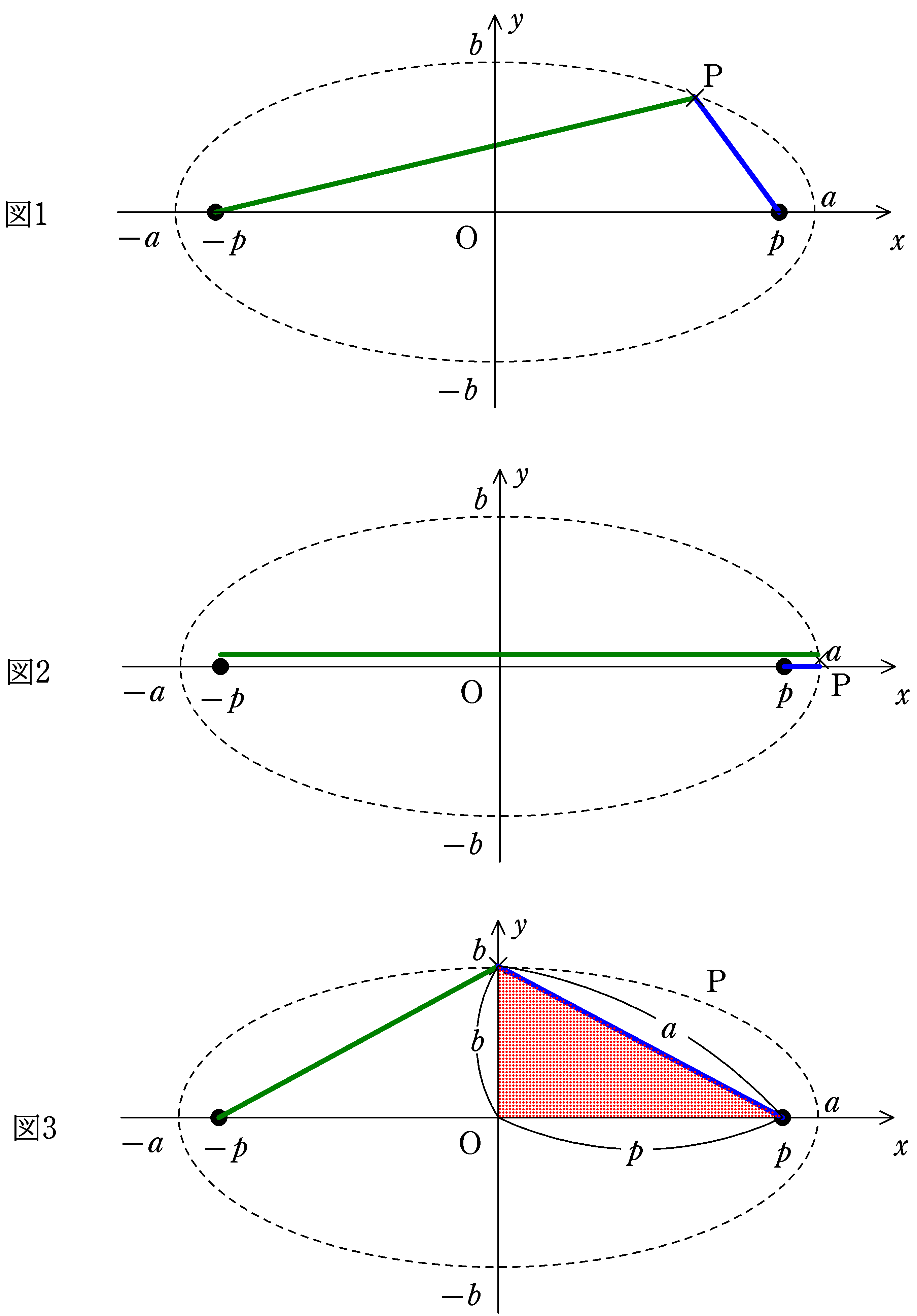
図2のように楕円上の点Pを$(a,0)$にもってくると
緑の線の長さ$=a-(-p)=a+p$
青の線の長さ$=a-p$
なので,
緑の線の長さ$+$青の線の長さ$=a+p+a-p=2a$
であり,2焦点からの距離の和は$2a$であることが確認できます.

PHYさん
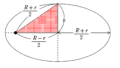
さらに,図3のように楕円上の点Pを$(0,b)$にもってくると,このとき,緑の線の長さと青の線の長さは等しいです.その和が$2a$なのだから,青の線の長さは$a$であることがわかります.図3の赤い部分の直角三角形について三平方の定理より
$p^{2}+b^{2}=a^{2}$
を確認できます.


コメント