[数学Ⅲ]物理の問題2 | Physicmath（フィジクマス）

NEKO

今回は束縛条件の問題です．

このくらいの問題は物理でも出題されます．

高校物理の問題なので，微分を使わないでも計算もできます．

問題

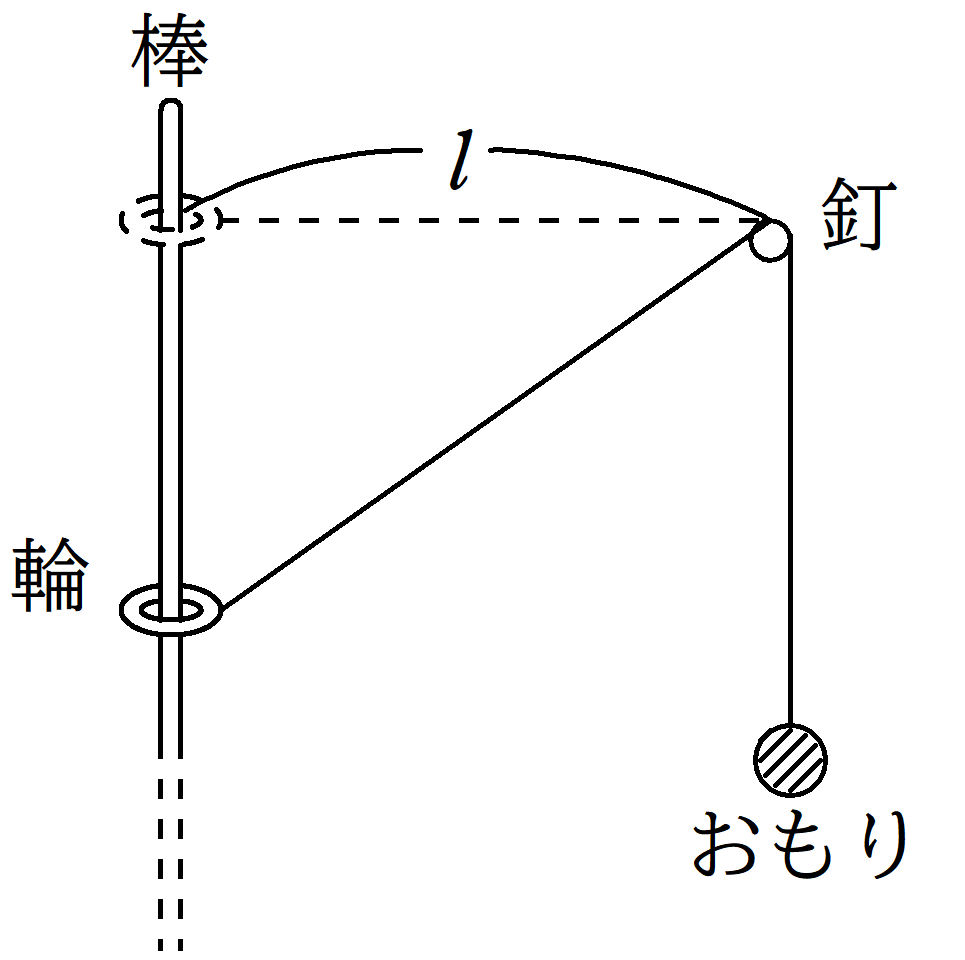
図のように，鉛直に立てた棒に質量$m$の輪を通し，輪に軽い糸をつけて，糸を棒から距離$l$だけ離れた釘にかけ，糸の先端に質量$M(>m)$のおもりをつけて鉛直に垂らしてある．糸と釘はなめらかであり，輪の位置は最初釘と同じ高さにあった状態から静かに手をはなした．このとき，次の問いに答えよ．

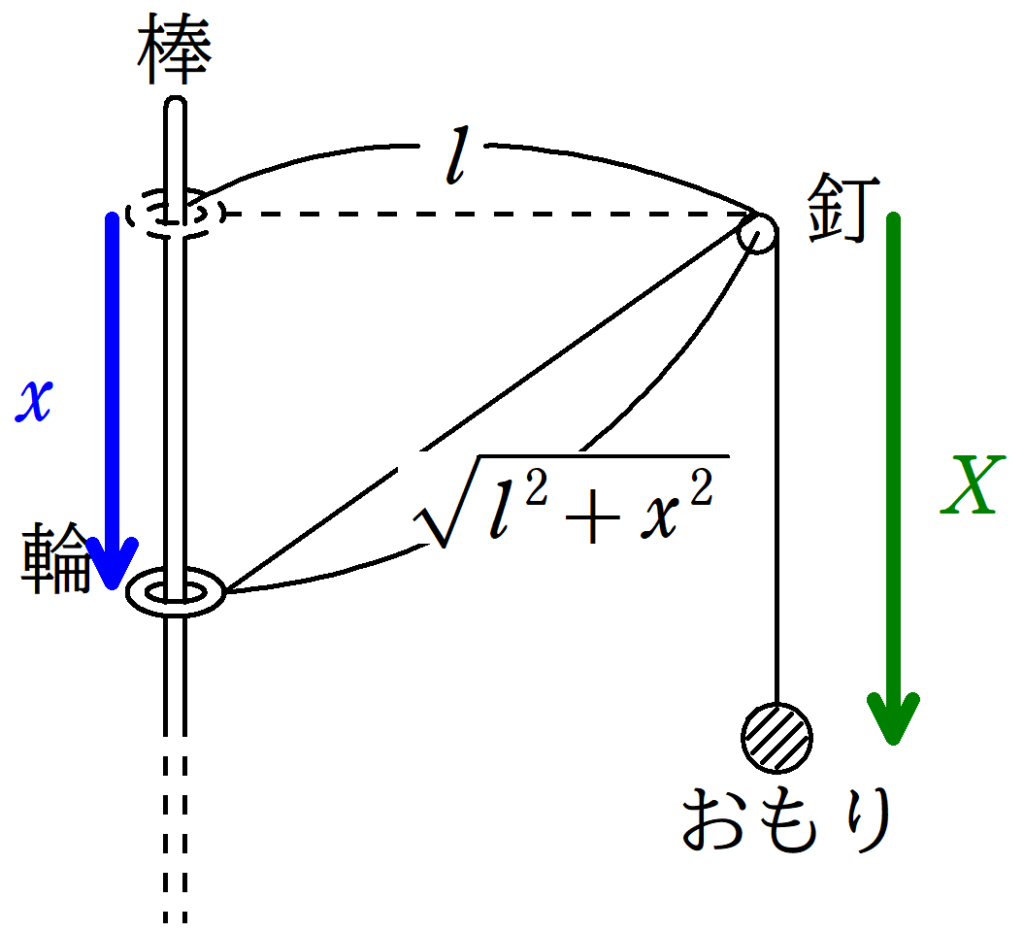
(1)　輪がはじめの位置から$x$だけ鉛直下方向にあるとき，おもりは釘より$X$だけ鉛直下方向にあった．糸の長さを$L$とするとき，$x$，$l$，$X$，$L$の関係式を立てよ．

(2)　(1)のとき，輪の速さ$v$とおもりの速さ$V$の関係式を求めよ．

<解答>

(1)

NEKO

図より，輪と釘の長さは$\sqrt{l^{2}+x^{2}}$です．

したがって，

$\sqrt{l^{2}+x^{2}}+X=L$　(答)　$\dots　(\ast)$

(2)　

NEKO

$(\ast)$の両辺を$t$で微分しましょう．

$\eqalign{(l^{2}+x^{2})^{\prime}\cdot \dfrac{1}{2}\cdot \dfrac{1}{\sqrt{l^{2}+x^{2}}}\cdot \dfrac{dx}{dt}+\dfrac{dX}{dt}&=0\cr \dfrac{dx}{dt}&=-\dfrac{\sqrt{l^{2}+x^{2}}}{x}\dfrac{dX}{dt}}$

したがって，

$v=\dfrac{\sqrt{l^{2}+x^{2}}}{x}V$　(答)