保存力と力学的エネルギー

保存力とは，経路によらず最初と最後の位置だけで仕事が決まる力のことを言います．

まずは，次の図のときを考えてみましょう．

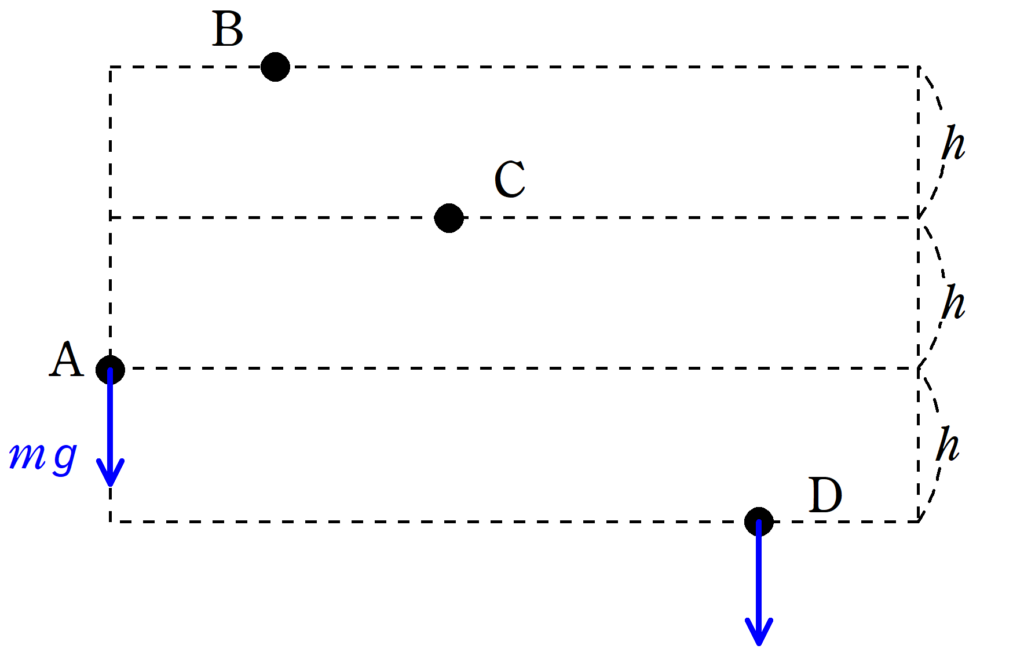
上図のとき，Aから直接Dの場所に行く場合の重力がする仕事$W_{1}$はどのくらいでしょうか？

そうですね．

では，A→B→C→Dまでに重力がした仕事$W_{2}$はいくらでしょう？

$W_{1}=W_{2}$となっていますね．

重力は最初と最後の位置が定まれば，どんな経路を描いても仕事が同じとなります．

このような経路によらない，保存力は次のものを覚えておけばよいでしょう．

• 重力
• 万有引力
• 弾性力
• 静電気力（クーロン力）
• 観測者が等加速度直線運動しているときの慣性力

摩擦力や張力，垂直抗力など，上にかいてあるもの以外の力です．

たとえば，摩擦力は短い経路と長い経路では，摩擦力がする仕事に差が出ます．

そうなんです．

保存力は最初と最後の位置で仕事が決まるので，あらかじめどの程度仕事をしてくれるのかがわかります．

次は位置エネルギーの話です．

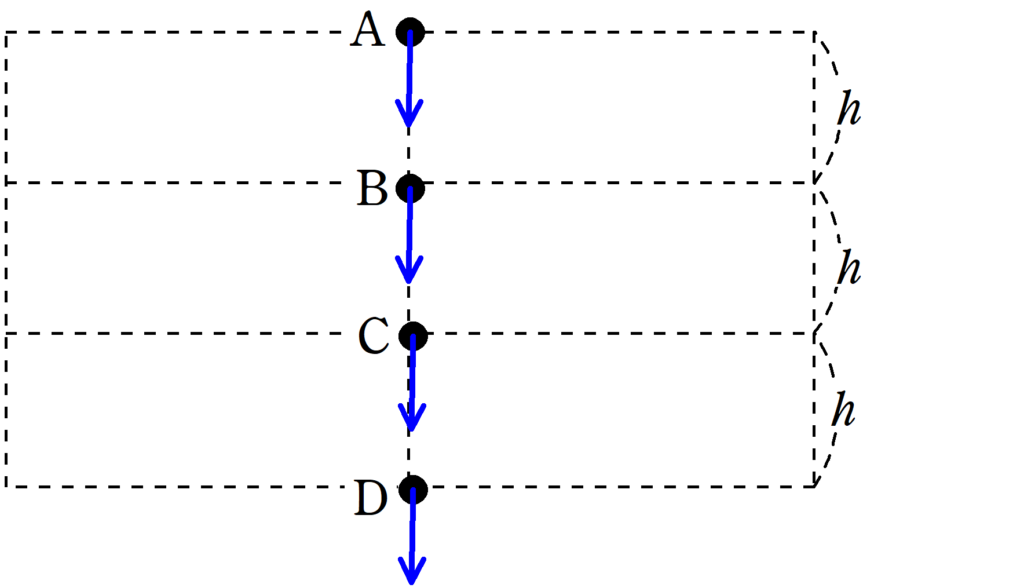
たとえば，Bの位置から見たときにAにある物体の重力がする仕事を考えてみましょう．

Aの位置にある物体にはたらく重力はどのような経路にせよ，Bにいくまでに$mgh$の仕事をすることが約束されています．

はい．この潜在的なエネルギーを位置エネルギー（ポテンシャルエネルギー）といいます．

Bからみれば，Aにある物体は$mgh$の位置エネルギーを持っています．

そうなります．

では，問題演習をやってみましょう．

保存力と同じ大きさの力を保存力の向きとは反対方向に外力が仕事をした分だけ位置エネルギーが蓄えられます．

これは結構間違う人が多いのですが，結論から言うと動きます．

力の和が0であることは加速度が0であって，速度が0であるとは言えません．

運動方程式

$ma=F$

からもわかると思います．

そういうことです．

要は運動エネルギーが変化しないようにしたいんです．

エネルギーの原理を考えれば，

$\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=$外力がした仕事

でした．

そういうことです．

さらに，$W_{保存力}$と位置エネルギーの変化$\Delta U$の関係について考えましょう．

たとえば，AからBに移動するときを考えましょう．

AからBに移動する間に重力がした仕事$W_{1}$

はいくらでしょう？

また，AからBに移動する間の位置エネルギーの変化$\Delta U_{1}$

はいくらでしょう？

それでは，BからAに移動する場合を考えましょう．

BからAに移動する間に重力がした仕事$W_{2}$と，位置エネルギーの変化$\Delta U_{2}$を求めてください．

そうなんです．

保存力が正の仕事をした分，位置エネルギーが使われてしまい，保存力が負の仕事をすると，位置エネルギーが蓄えられます．

$(\ast)$の$W_{保存力}=-W_{外力}$と$(2\ast)$の$\Delta U=-W_{保存力}$から次の式を得ます．

$\Delta U=W_{外力}$

それでは，最後に運動エネルギーの原理を変形しておしまいにしましょう．