
前回の内容はこちらです.
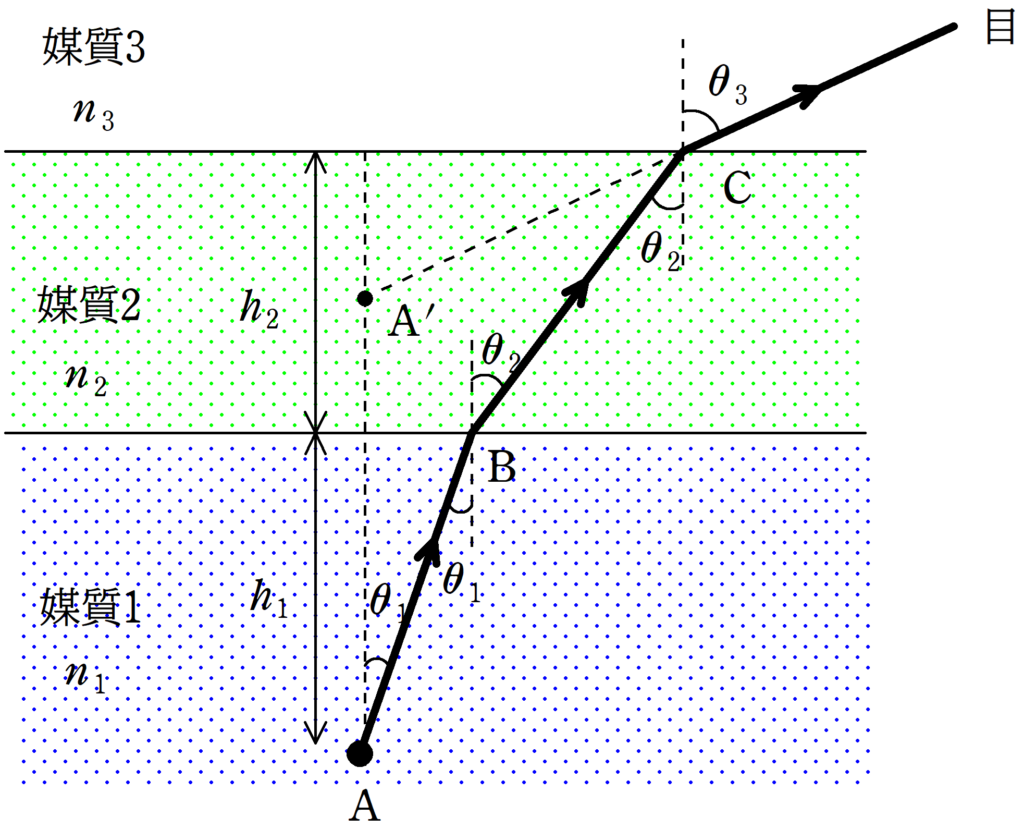
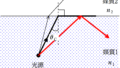
図のように,絶対屈折率$n_{1}$,$n_{2}$,$n_{3}$の媒質1,2,3がある.ただし,$n_{1}>n_{2}>n_{3}$とする.媒質1中の点Aに光源をおき,Aの真上付近の媒質3より媒質2の方を眺めると,光源は媒質2中の点$\rm A^{\prime}$に浮き上がっているように見えた.Aと媒質1と2の境界までの距離を$h_{1}$,媒質2の厚さを$h_{2}$とする.また,光源から出た光は,媒質2に角度$\theta_{1}(<90^{\circ})$で入射し,屈折角は$\theta_{2}$であった.さらに,光は進み,媒質3へ角度$\theta_{2}$で入射し,屈折角は$\theta_{3}$であった.このとき,次の問いに答えよ.
(1) $n_{1}$,$n_{2}$,$n_{3}$,$\theta_{1}$,$\theta_{2}$,$\theta_{3}$の関係式を答えよ.
(2) 媒質3の境界と$\rm A^{\prime}$との距離$h$を$h_{1}$,$h_{2}$,$\theta_{1}$,$\theta_{2}$,$\theta_{3}$を用いて表せ.
(3) $\theta$が非常に小さいとき,$\tan\theta \fallingdotseq \sin\theta\fallingdotseq \theta$の近似が適用できる.$\theta_{1}$,$\theta_{2}$,$\theta_{3}$にこの近似が適用できるとき,$h$を,$n_{1}$,$n_{2}$,$n_{3}$,$h_{1}$,$h_{2}$を用いて表せ.
<解答>
(1)

屈折の法則を確認しましょう.
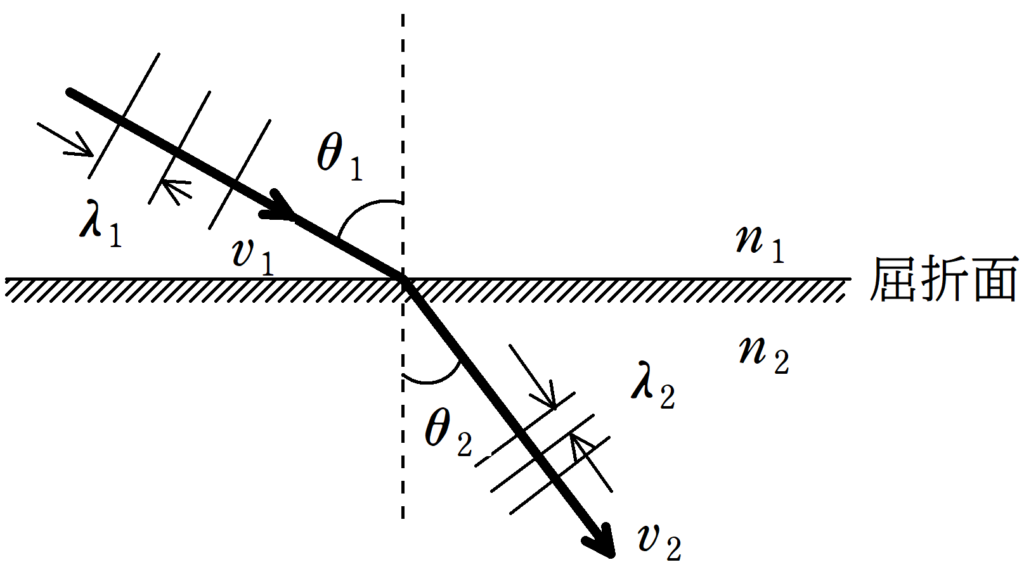
速さ$v_{1}$,波長$\lambda_{1}$の波が入射角$\theta_{1}$で屈折面に入射し,その後屈折角が$\theta_{2}$,速さ$v_{2}$,波長が$\lambda_{2}$となった.入射側の媒質の屈折率を$n_{1}$,屈折する側の媒質の屈折率を$n_{2}$とすると,次の関係が成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\sin\theta_{1}}{\sin\theta_{2}}$
また,屈折により,媒質の振動数$f$および周期$T$は変化しないことから,次のことが成り立つ.
$\dfrac{v_{1}}{v_{2}}=\dfrac{\cancel{f}\lambda_{1}}{\cancel{f}\lambda_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}$
一方,屈折率との関係は次のようになる.
$n_{1}\sin\theta_{1}=n_{2}\sin\theta_{2}$
$n_{1}v_{1}=n_{2}v_{2}$
$n_{1}\lambda_{1}=n_{2}\lambda_{2}$
最後に,$n_{12}=\dfrac{n_{2}}{n_{1}}$を屈折率$n_{1}$の媒質に対する屈折率$n_{2}$の媒質の相対屈折率という.

屈折率が混ざった式は
$n\times$★=一定
の式が便利です.
$n_{1}\sin\theta_{1}=n_{2}\sin\theta_{2}=n_{3}\sin\theta_{3}$ (答)
(2)
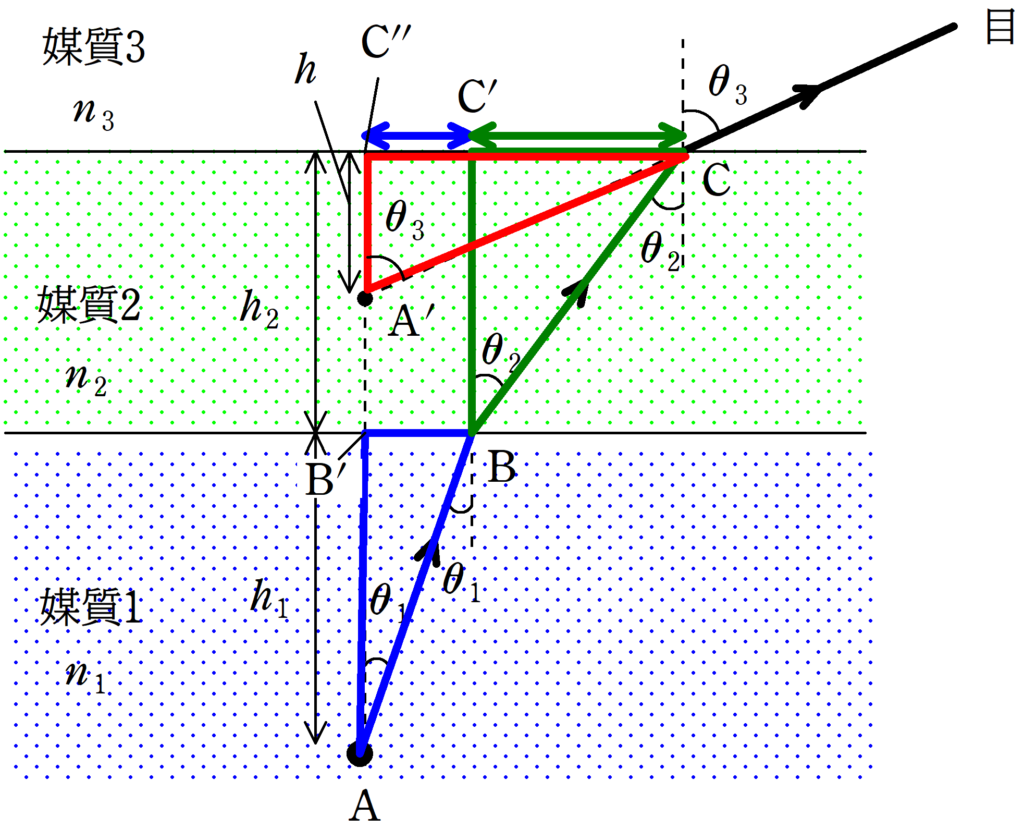

上図の青の直角三角形(三角形$\rm ABB^{\prime}$)と,緑の直角三角形(三角形$\rm BCC^{\prime}$)と,赤の直角三角形(三角形$\rm A^{\prime}CC^{\prime\prime}$)について考えます.
★ $\rm BB^{\prime}+CC^{\prime}=CC^{\prime\prime}$より
$h_{1}\tan\theta_{1}+h_{2}\tan\theta_{2}=h\tan\theta_{3}$
$\therefore h=\dfrac{\tan\theta_{1}}{\tan\theta_{3}}h_{1}+\dfrac{\tan\theta_{2}}{\tan\theta_{3}}h_{2}$ (答)
(3)

(1)の結果を近似式を用いて次のように変形しましょう.
$n_{1}\sin\theta_{1}=n_{3}\sin\theta_{3}$より
$\dfrac{\sin\theta_{1}}{\sin\theta_{3}}=\dfrac{n_{3}}{n_{1}}$
したがって,
$\dfrac{\tan\theta_{1}}{\tan\theta_{3}}\fallingdotseq\dfrac{n_{3}}{n_{1}}$ $\cdots (\ast)$
また,$n_{2}\sin\theta_{2}=n_{3}\sin\theta_{3}$より
$\dfrac{\sin\theta_{2}}{\sin\theta_{3}}=\dfrac{n_{3}}{n_{2}}$
したがって,
$\dfrac{\tan\theta_{2}}{\tan\theta_{3}}\fallingdotseq\dfrac{n_{3}}{n_{2}}$ $\cdots (2\ast)$
$(\ast)$,$(2\ast)$を(2)の結果に代入すると
$h\fallingdotseq \dfrac{n_{3}}{n_{1}}h_{1}+\dfrac{n_{3}}{n_{1}}h_{2}$ (答)



コメント
[…] https://physicmath.net/5913/,5913,physicmath.net投稿,publish 波動演習問題演習問題(基本)高校物理 シェアする Twitter Facebook はてブ LINE physicmathをフォローする physicmath Physicmath(フィジクマス) […]