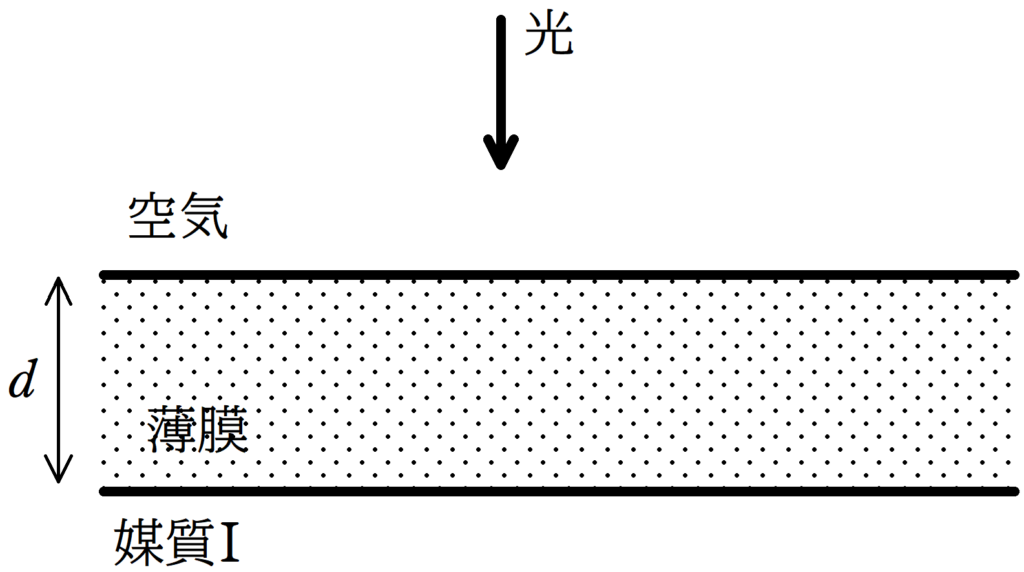
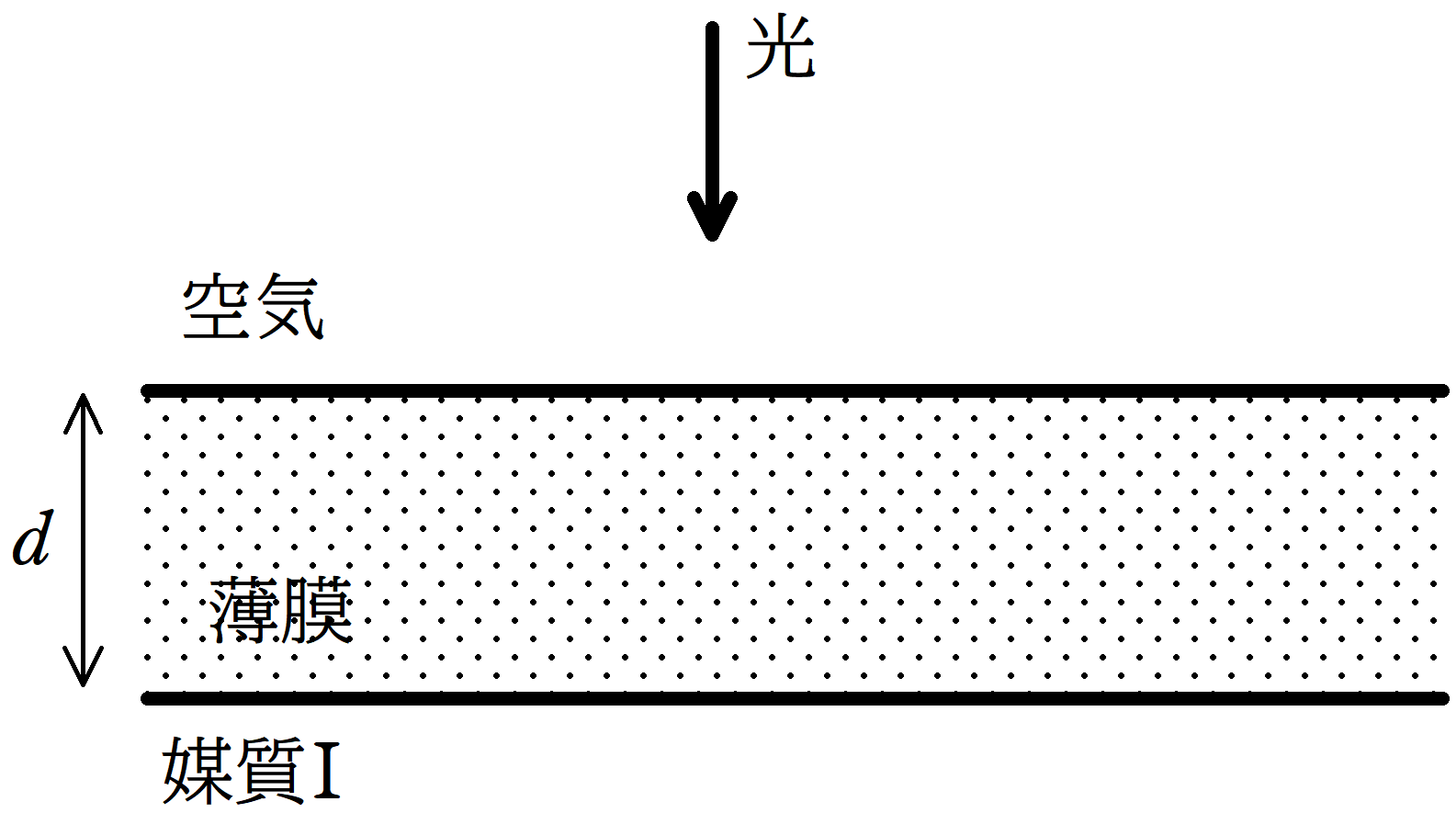
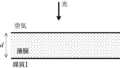
厚さ$d$,空気に対する相対屈折率$n(>1)$の薄膜に垂直に入射した光の反射による干渉について考える.ただし,$d$は十分小さい.空気側から薄膜に向けて光を垂直に当てたとき,光の一部は反射され,一部は薄膜に透過し,媒質Iの境界で反射されたのち,再び空気にもどっていった.このとき,次の問いに答えよ.ただし,空気中での光の波長を$\lambda_{0}$とする.
(1) 媒質Iが空気であるとき,強め合いの条件と弱め合いの条件を$\lambda_{0}$,$d$,$n$,自然数$m$を用いてかけ.
(2) 媒質Iの空気に対する屈折率が$n^{\prime}(>n)$のとき,強め合いの条件と弱め合いの条件を$\lambda_{0}$,$d$,$n$,自然数$m$を用いてかけ.
<解答>

位相差による干渉条件を確認していきましょう.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

また,固定端反射なのか自由端反射なのかは次の図で確認していきましょう.
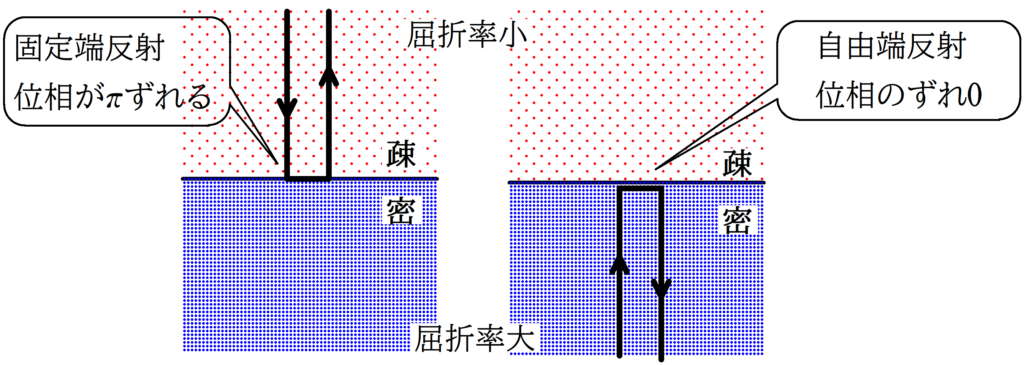
(1)

空気から薄膜での反射は,屈折率が小さい方から大きい方への反射なので固定端反射です.つまり,位相が$\pi$ずれます.
一方,薄膜から空気での反射は屈折率が大きい方から小さい方への反射なので,自由端反射です.つまり,位相のずれなしです.
すなわち,反射に位相のずれは総合で$\pi$ずれます.
また,距離の差は,$2d$なので,距離による位相差は,薄膜中の波長が$\dfrac{\lambda}{n}$であることを考慮して
$\dfrac{2\pi}{\dfrac{\lambda}{n}}\cdot 2d$
したがって,位相差を$\varDelta \varphi$として,強め合いの条件は
$\varDelta \varphi=2\pi m$
$\dfrac{4\pi nd}{\lambda}+\pi =2\pi m$ (答)

$2d=\left(m-\dfrac{1}{2}\right)\cdot \dfrac{\lambda}{n}$ともかけるね.
弱め合いの条件は
$\varDelta\varphi=(2m+1)\pi$
$\therefore \dfrac{4\pi nd}{\lambda}+\pi=(2m+1)\pi$

ここで,$\varDelta \varphi=(2m-1)\pi$とはしないようにしましょう.
$m=1$のとき,
$\dfrac{4\pi nd}{\lambda}=0$
となり,辻褄があわなくなります.

弱め合いの条件は
$2d=m\cdot \dfrac{\lambda}{n}$
ともかけるね.
(2)

(2)では,空気と薄膜および,薄膜と媒質Iの間のどちらでも固定端反射をするので,結局反射による
位相のずれは0となります.
つまり,(1)の強め合いと弱め合いの条件が逆になりますね.
強め合いの条件
$\varDelta \varphi=2\pi m$
$\dfrac{4\pi nd}{\lambda}=2\pi m$ (答)
弱め合いの条件
$\varDelta\varphi=(2m-1)\pi$
$\therefore \dfrac{4\pi nd}{\lambda}=(2m-1)\pi$ (答)

こちらは右辺を$(2m+1)\pi$とすると,$m=1$のとき,$3\pi$になり,$\pi$が表現できないため,$(2m-1)\pi$とする必要があるんだね.

次回の内容はこちらです.


コメント
[…] [干渉問題]薄膜の干渉1問題厚さ$d$,空気に対する相対屈折率$n(>1)$の薄膜… 問題 […]