
今回は,単振り子の問題です.
振り子運動の中でも振幅が微小なものを考えます.
まずは,基本事項の確認です.
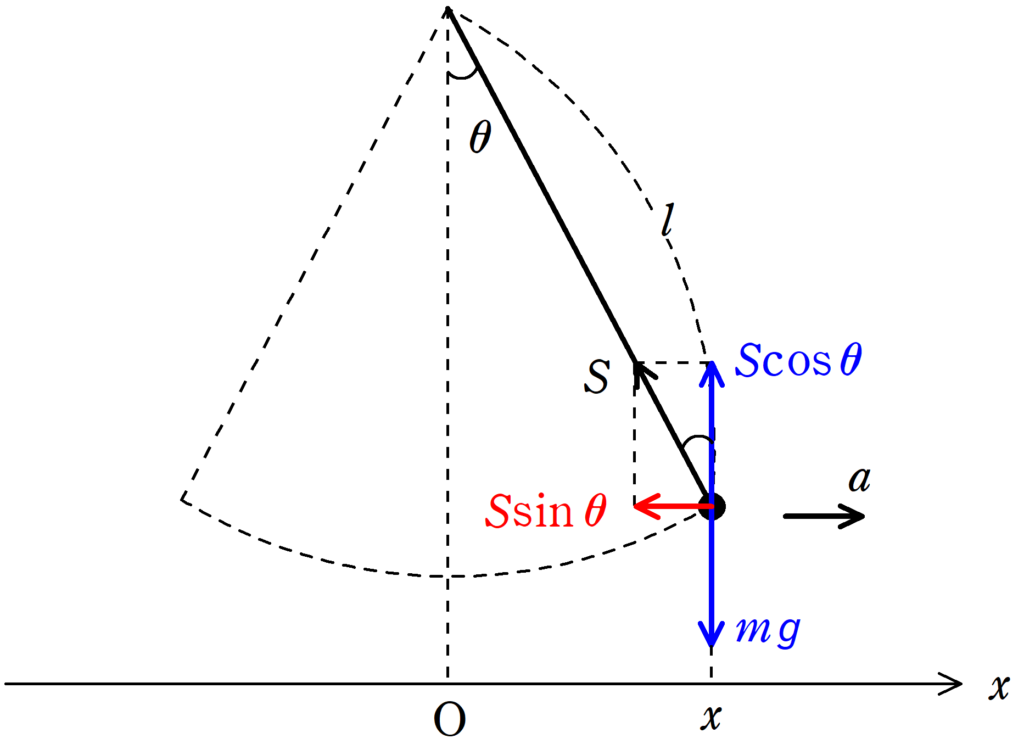

上図のように,長さ$l$の糸にくくりつけられた質量$m$の物体の単振り子運動を考えます.
物体が運動しているとき,位置$x$にいるときの物体の加速度を$a$とします.
図は物体が$x>0$にあるときのことを考えています.
物体にはたらく力は重力$mg$と張力$S$($S>0$)です.
張力を鉛直方向と水平方向に分解すると
水平負の方向に$S\cos\theta$と鉛直上向きに$S\sin\theta$となります.
ここで近似です.
$\clubsuit$2つの近似$\clubsuit$
- 鉛直方向はほとんど動いていないので,常につり合っているとみなす.
- $|\theta|\ll 1$のとき$\cos\theta\approx 1$

では,鉛直方向のつり合いの式と水平方向の運動方程式を立てましょう.
★鉛直方向のつり合いの式
$S\cos\theta =mg$
$\cos\theta \approx 1$より
$S\approx mg$ $\dots (\ast)$
★水平方向の運動方程式
$ma=-S\sin\theta$
$(\ast)$より,$S=mg$を代入して
$ma=-mg\sin\theta$
また,$x=l\sin\theta$の関係を上式に入れて
$mas=-mg\cdot \dfrac{x}{l}=-\dfrac{mg}{l}x$ $\dots (2\ast)$

運動方程式から,中心が$x=0$で角振動数$\omega=\sqrt{\dfrac{g}{l}}$,周期$T=2\pi\sqrt{\dfrac{l}{g}}$の単振動であることがわかるね.

それでは,単振り子の問題を解いてみましょう.
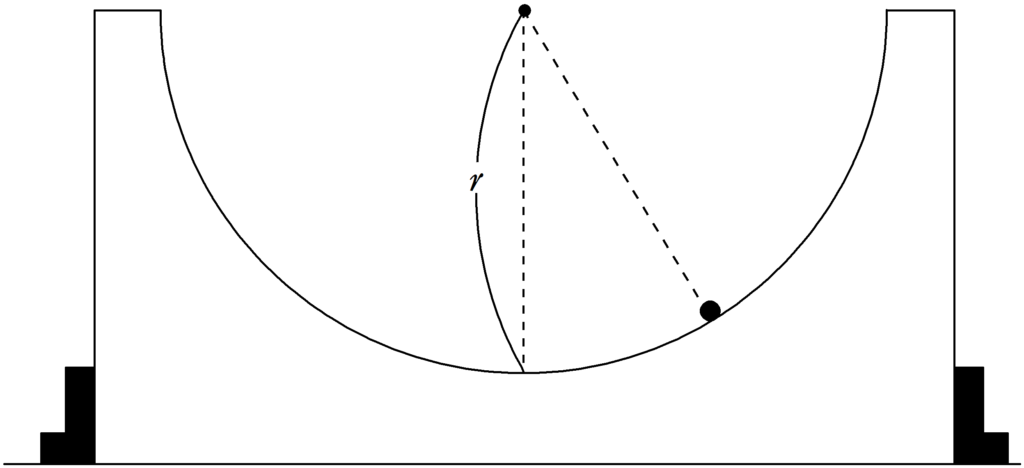
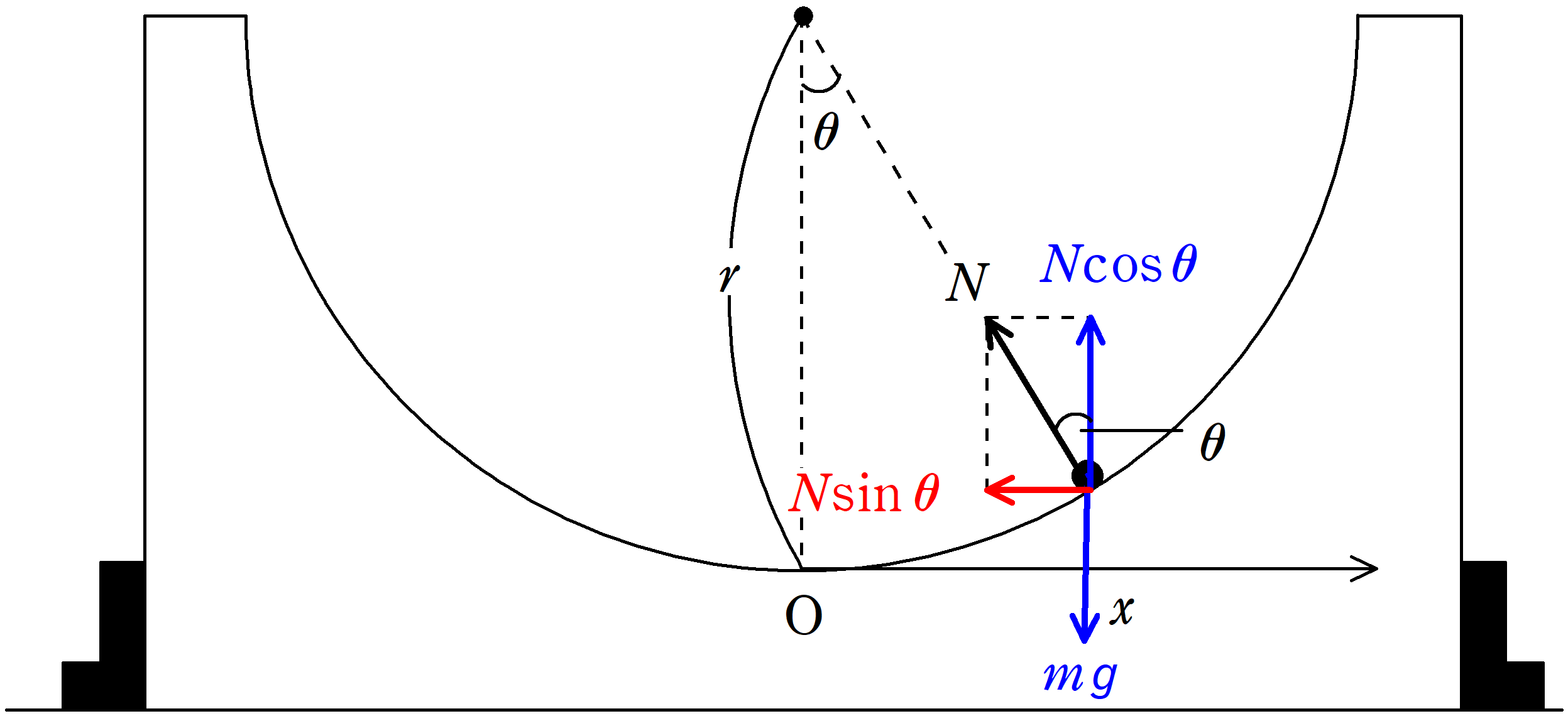
図のように,水平な床の上に台が固定されている.
この台は半径$r$の円形状のなめらかなすべり面がある.
このすべり面の最下点の位置から少しずらした場所に質量$m$の大きさの無視できる物体を静かに置いたところ,単振動した.
このときの単振動の周期を求めよ.
<解答>

さきほどの糸による張力が垂直抗力になっただけだね.
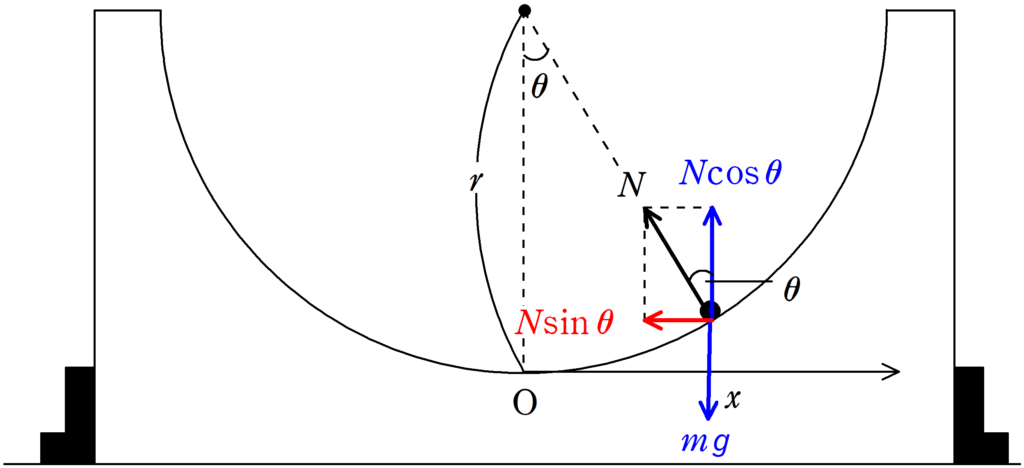

図のように座標をとります.
同じく上図では$x>0$のときです.
物体が位置$x$にあるときの加速度を$a$としましょう.
また,物体にはたらく垂直抗力の大きさを$N$として,$x$軸方向と,それに垂直な方向に分解します.
そして,鉛直方向がつり合っていると近似して,鉛直方向のつり合いの式と$x$軸方向の運動方程式を立てます.
★ 鉛直方向のつり合いの式
$N\cos\theta =mg$
微小な振幅の振動なので,$\cos\theta\approx 1$より
$N\approx mg$ $\dots (\heartsuit)$
★ $x$軸方向の運動方程式
$ma=-N\sin\theta$
$(\heartsuit)$より
$ma=-mg\sin\theta$
また,$x=r\sin\theta$より
$ma=-mg\cdot \dfrac{x}{r}=-\dfrac{mg}{r}x$
したがって,物体の角振動数$\omega$と周期$T$は
$\omega=\sqrt{\dfrac{g}{r}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{r}{g}}$
したがって,答えは$T=2\pi\sqrt{\dfrac{r}{g}}$です.

単振り子は,近似の仕方がポイントだよ.
実は別な近似の仕方もあるので,最後に紹介しておくね.
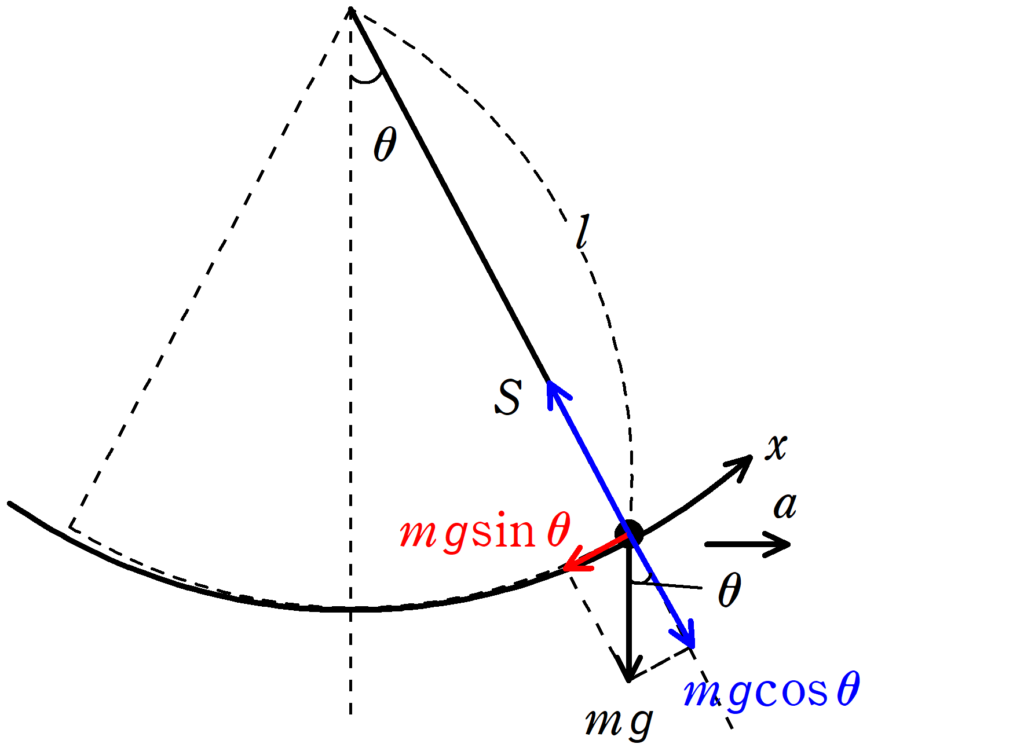

上図のように軌道にそって$x$軸をとります.
重力を軌道の方向とそれに対して垂直な方向に分解して,軌道の方向の運動方程式を立てます.
★ 運動方程式
$ma=-mg\sin\theta$
$|\theta|\ll 1$のとき$\sin\theta \approx \theta$の近似式を使って
$ma \approx -mg\theta$ $\dots (\spadesuit)$
また,円の弧の長さと半径と中心角の関係より
$x=l\theta$ $\therefore \theta =\dfrac{x}{l}$
これを$(\spadesuit)$に代入して
$ma=-mg\cdot \dfrac{x}{l}=-\dfrac{mg}{l}x$

これで同じ形の運動方程式になりました!


コメント
[…] […]
[…] [標準]単振動演習⑧や[標準]単振動演習⑨があります. […]