
前回に引き続き単振り子の問題です.
今回は少しだけ応用です.
前回の内容はこちら.

また,今回は慣性力の問題でもあるので,慣性力の復習しておきます.
加速度運動している観測者が物体をみたときに見かけの力がはたらく.
これを慣性力とよぶ.
観測者の加速度を$A$,物体の質量を$m$とすると,慣性力は
$m\cdot (-A)$
である.
つまり,観測者の加速度とは逆方向に大きさ$m|A|$の力がはたらく.

それでは問題演習です.
今回は2題あります!
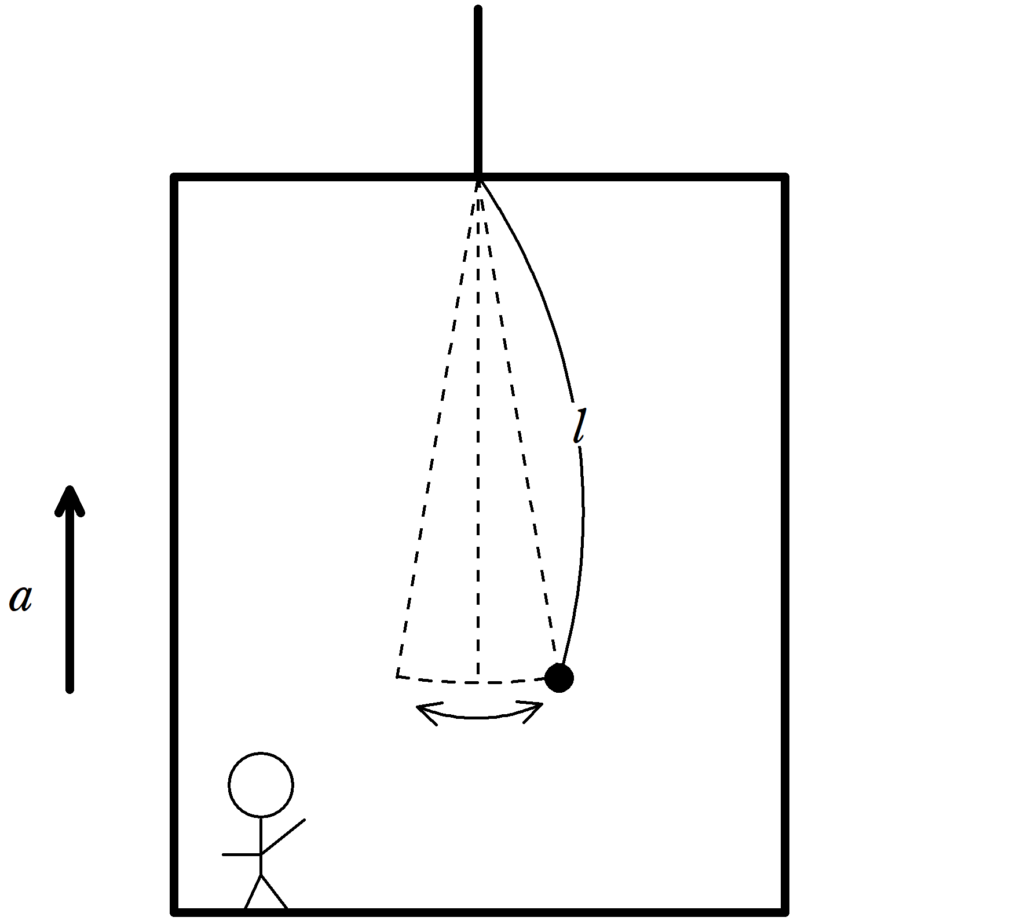
鉛直上向きに大きさ$a$の加速度で運動をしているエレベーターの中からみた単振り子運動を考える.
糸の長さを$l$,物体の質量を$m$としてエレベーターの中から見た単振り子の周期を求めよ.
ただし,重力加速度の大きさを$g$とし,この単振り子の振れの角度は非常に小さいとしてよい.
<解答>

エレベーターの中からみた物体にはたらく力を考えましょう.
まずは,重力$mg$.
鉛直下向きにはたらきますね.
そして,糸の張力.張力の大きさを$S$としましょう.
最後に,観測者自身が加速度$a$で鉛直上向きに運動をしているので,鉛直下向きに大きさ$ma$の慣性力がはたらきます.
ここで,鉛直下向きにはたらく力は重力と慣性力となり,その合力は$m(g+a)$となります.このとき,$m(g+a)$をみかけの重力といいます.
つまり,今までの重力を$mg$から$m(g+a)$と書き換えて問題を考えればよいのです.
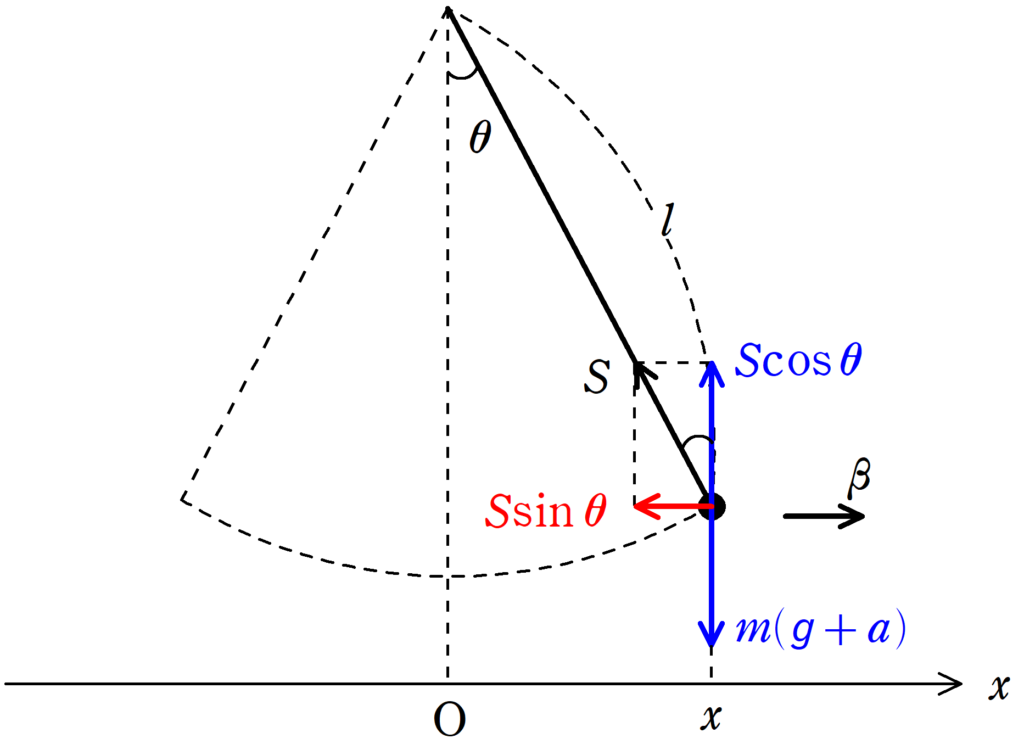

上図のように座標をとりましょう.
この座標はエレベーター内に座標をとりました.
位置$x$における加速度を$\beta$とします.

張力を$x$軸に平行な方向と垂直な方向に分解しましょう.
そして,$x$軸に垂直な方向はつり合っていると近似をして,つり合いの式を立てます.
$x$軸方向は運動方程式です.
★ $x$軸に垂直な方向のつり合いの式
$S\cos\theta=m(g+a)$
$|\theta|\ll 1$のとき,$\cos\theta \approx 1$より
$S\approx m(g+a)$ $\dots (\ast)$
★ $x$軸方向の運動方程式
$m\beta =-S\sin\theta$
$(\ast)$より
$m\beta =-m(g+a)\sin\theta$
また,$\sin\theta =\dfrac{x}{l}$より
$m\beta =-m(g+a)\cdot \dfrac{x}{l}=-\dfrac{m(g+a)}{l}x$
したがって,角振動数$\omega$と周期$T$は
$\omega=\sqrt{\dfrac{g+a}{l}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l}{g+a}}$
答えは,$T=2\pi\sqrt{\dfrac{l}{g+a}}$です.

さあ,もう1問です!
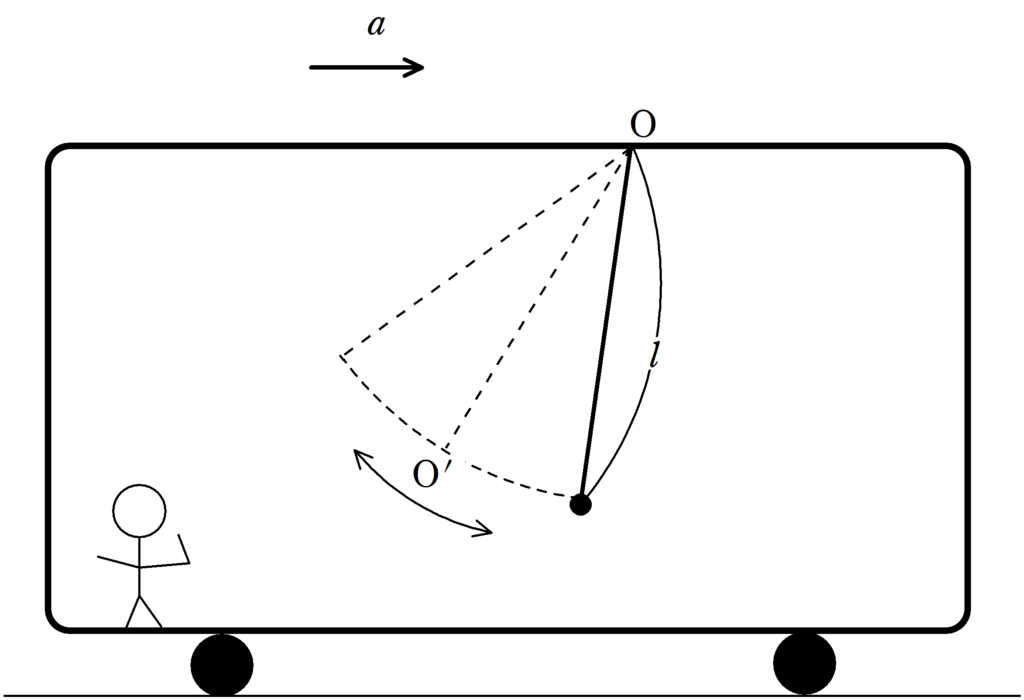
電車の中からみた振り子運動を考える.
糸の一端を電車の天井$\rm O$に固定し,さらにもう一端を物体にとりつける.
糸の長さを$l$,物体の質量を$m$,重力加速度の大きさを$g$とする.
(1) 電車の加速度を少しずつ大きくしていって,加速度が水平右方向に大きさ$a$になったとき,$\rm O$と電車の中からみて静止している物体の位置$\rm O^{\prime}$を結ぶ$\rm OO^{\prime}$の鉛直線からのなす角を$\alpha$とする.このとき,$\tan \alpha$を$g$と$a$を用いて表せ.
(2) (1)で静止している位置から物体を糸をたるませず引き上げて手をはなしたところ単振動をはじめた.
この単振動の周期を求めよ.
<解答>

さあ,今度は慣性力は左方向にはたらきます.
大きさは同じく$ma$です.
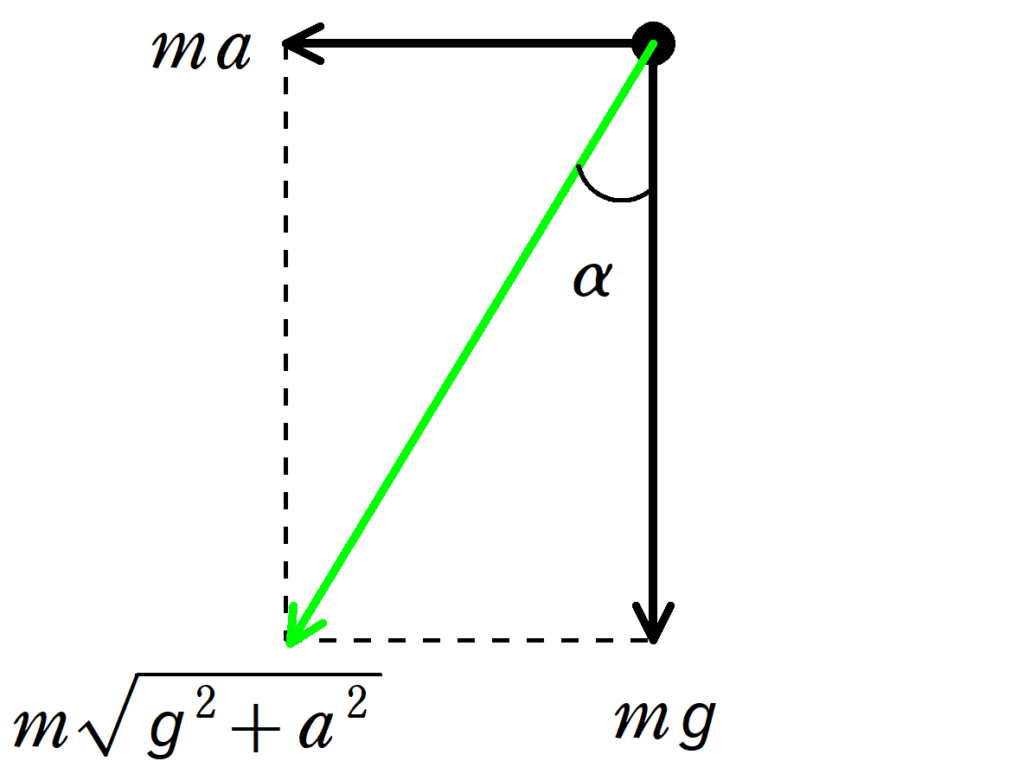

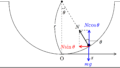
そして,重力と慣性力の合力である見かけの重力を考えます.
上図のように,力を合成すれば見かけの重力の大きさは
$m\sqrt{g^{2}+a^{2}}$
となります.
そして,見かけの重力の鉛直線からのなす角を$\alpha$とすると,
$\tan\alpha=\dfrac{ma}{mg}=\dfrac{a}{g}$
となります.
ということで,(1)の答えは$\tan \alpha=\dfrac{a}{g}$です.
(2)

下図のように座標をとりましょう.
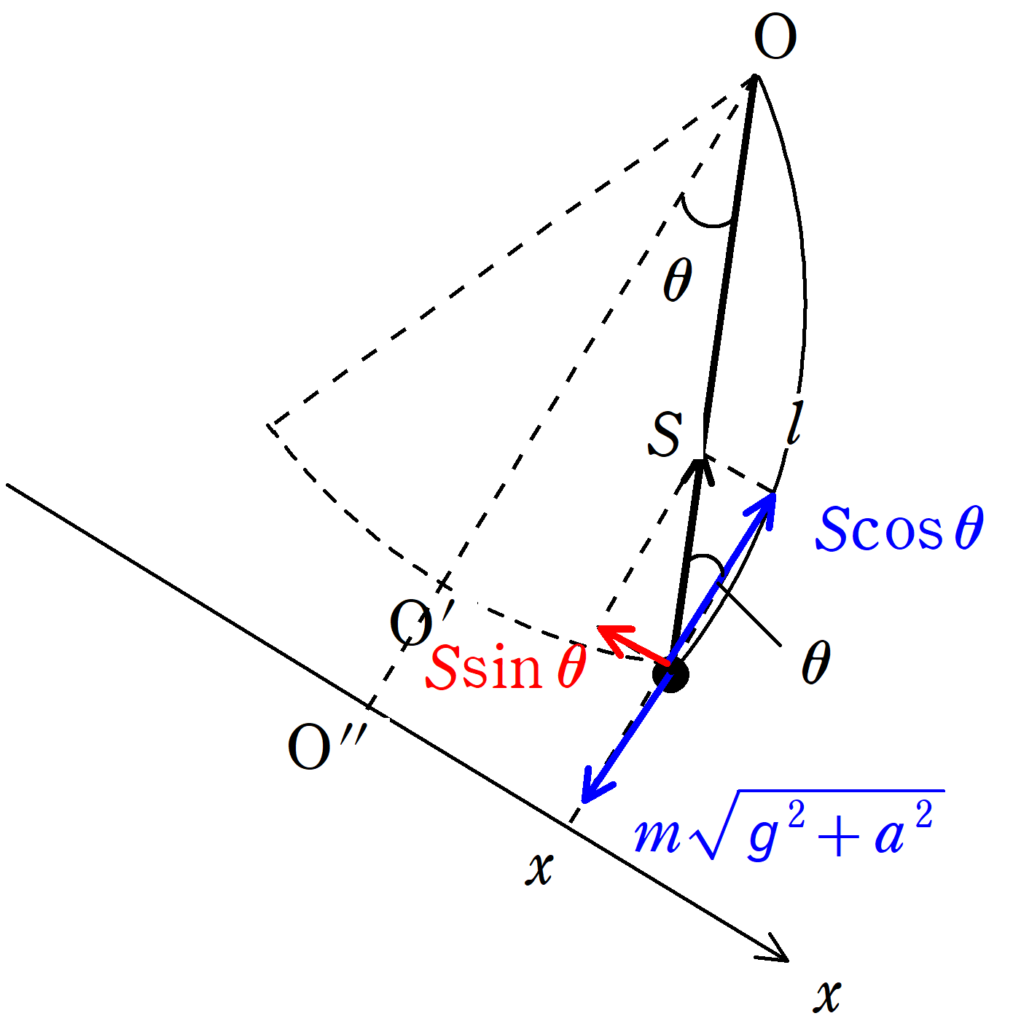

上図では,みかけの重力と垂直な方向に$x$軸をとっています.
上図だと少々見にくい場合は,次のように書き直すとよいでしょう.
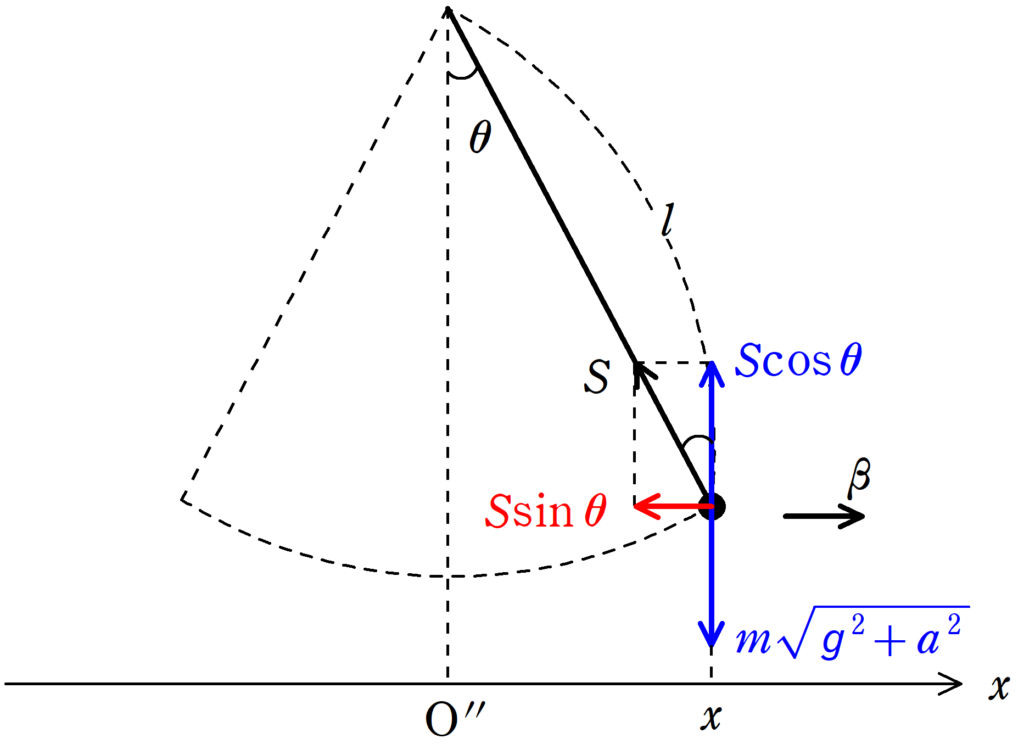

同じく,みかけの重力方向はつり合っていると近似します.
そして,$x$軸方向の運動方程式を立てます.加速度は$\beta$としましょう.
★ みかけの重力方向のつり合いの式
$S\cos\theta=m\sqrt{g^{2}+a^{2}}$
$\cos\theta \approx 1$として
$S\approx m\sqrt{g^{2}+a^{2}}$ $\dots (2\ast)$
★ $x$軸方向の運動方程式
$m\beta =-S\sin\theta$
$(2\ast)$を代入して
$m\beta =-m\sqrt{g^{2}+a^{2}}\sin\theta$
また,$\sin\theta =\dfrac{x}{l}$より
$m\beta =-m\sqrt{g^{2}+a^{2}}\cdot \dfrac{x}{l}$
$m\beta=-\dfrac{m\sqrt{g^{2}+a^{2}}}{l}x$
したがって,角振動数$\omega$と周期$T$は
$\omega=\sqrt{\dfrac{\sqrt{g^{2}+a^{2}}}{l}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{l}{\sqrt{g^{2}+a^{2}}}}$
したがって,答えは$T=2\pi\sqrt{\dfrac{l}{\sqrt{g^{2}+a^{2}}}}$

以上で今回はおしまいです!


コメント