
運動方程式演習①基礎編のスタートです.
基礎編ははじめて物理を勉強する方にもおすすめです!
質量$m$の物体に力$F$がはたらいているとき,物体の加速度$a$をすると,次の関係式が成り立つ.
$ma=F$
これを運動方程式という.

まずは,運動方程式を立てる練習をしていきます.
運動方程式の立て方はイチから説明します.
運動方程式の立て方についてはこちらも参考にしてください.

では,問題を解いていきましょう.
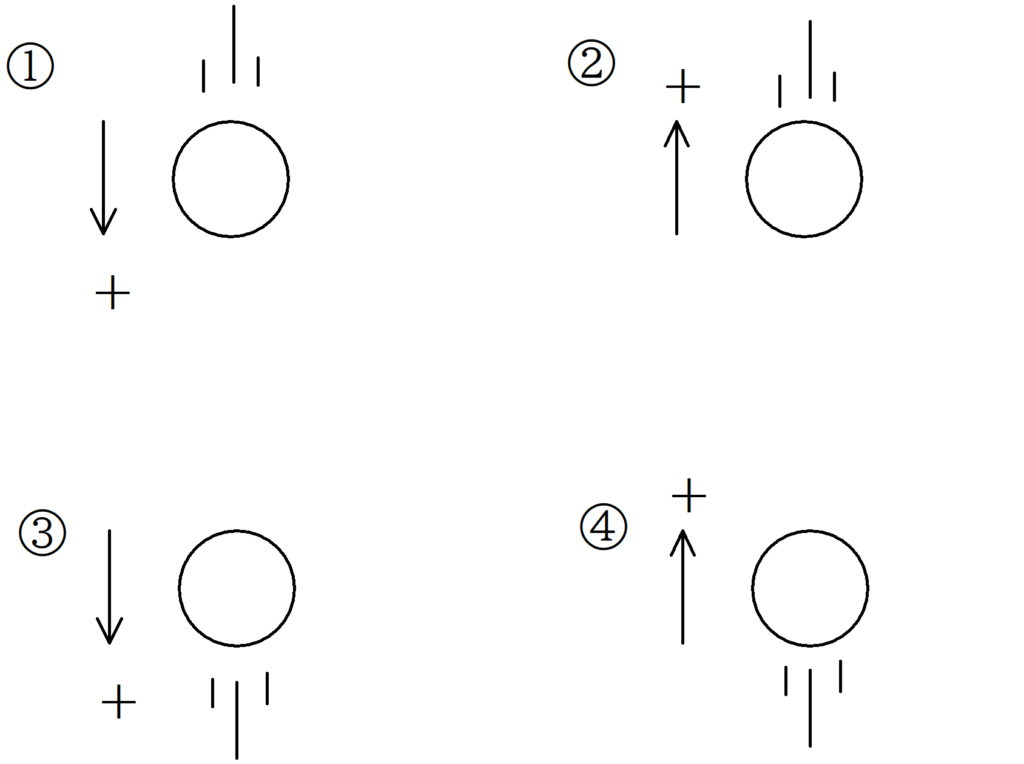
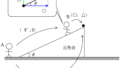
上図の①と②は質量$m$の物体が落下している様子,③と④は質量$m$の物体が上昇している様子を表している.
重力加速度の大きさを$g$とし,空気抵抗は無視をすることができるとして,次の問いに答えよ.
(1) ①の図において,鉛直下向きを正として加速度を$a$とするとき,運動方程式を立て,加速度を求めよ.
(2) ②の図において,鉛直上向きを正として加速度を$a$とするとき,運動方程式を立て,加速度を求めよ.
(3) ③の図において,鉛直下向きを正として加速度を$a$とするとき,運動方程式を立て,加速度を求めよ.
(4) ④の図において,鉛直上向きを正として加速度を$a$とするとき,運動方程式を立て,加速度を求めよ.
<解答>

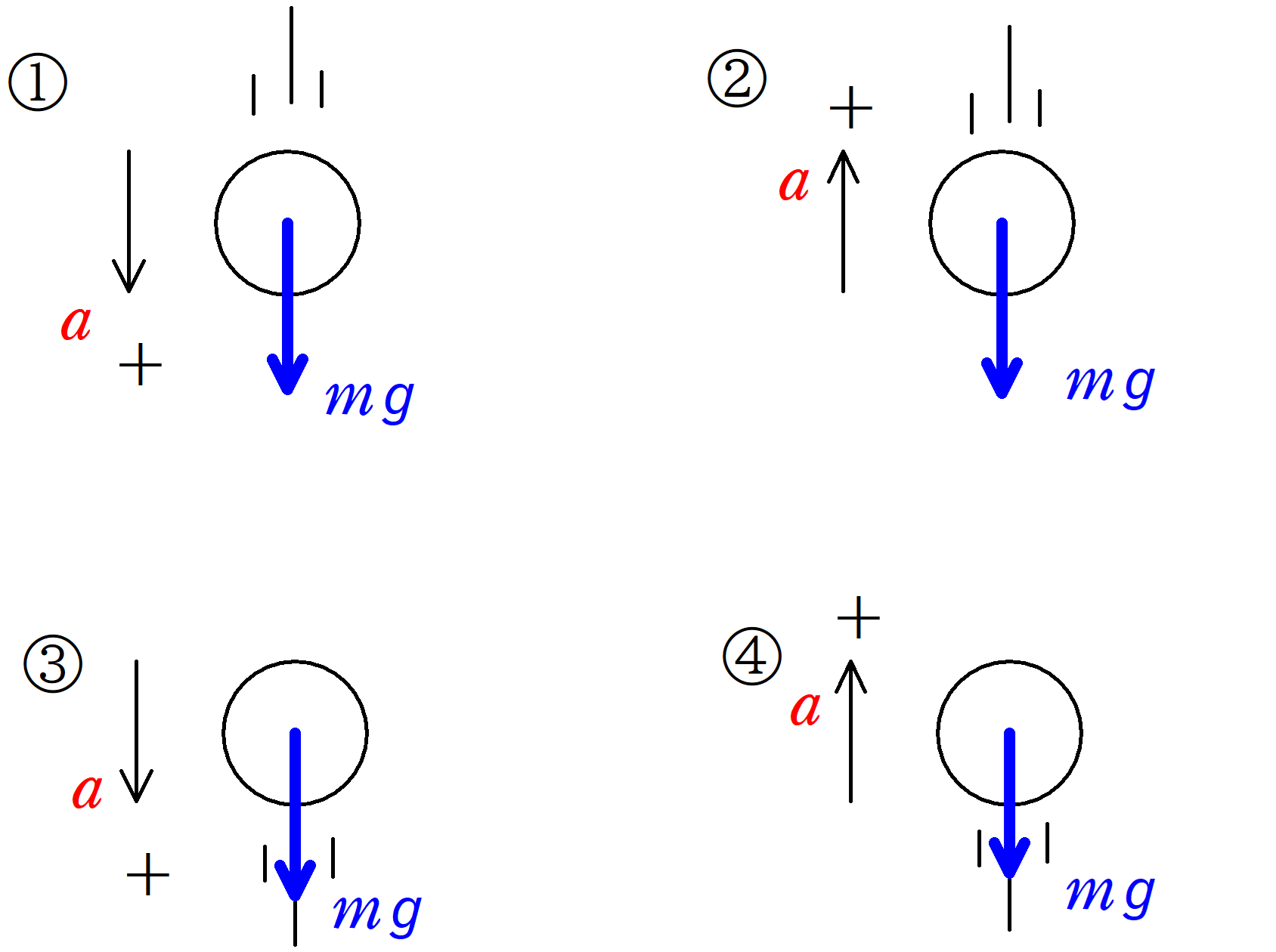
まずは,はたらく力を書いていこう.
注意してほしいのは,動く方向と関係なく,鉛直下向きに大きさ$mg$の力がはたらくことです.
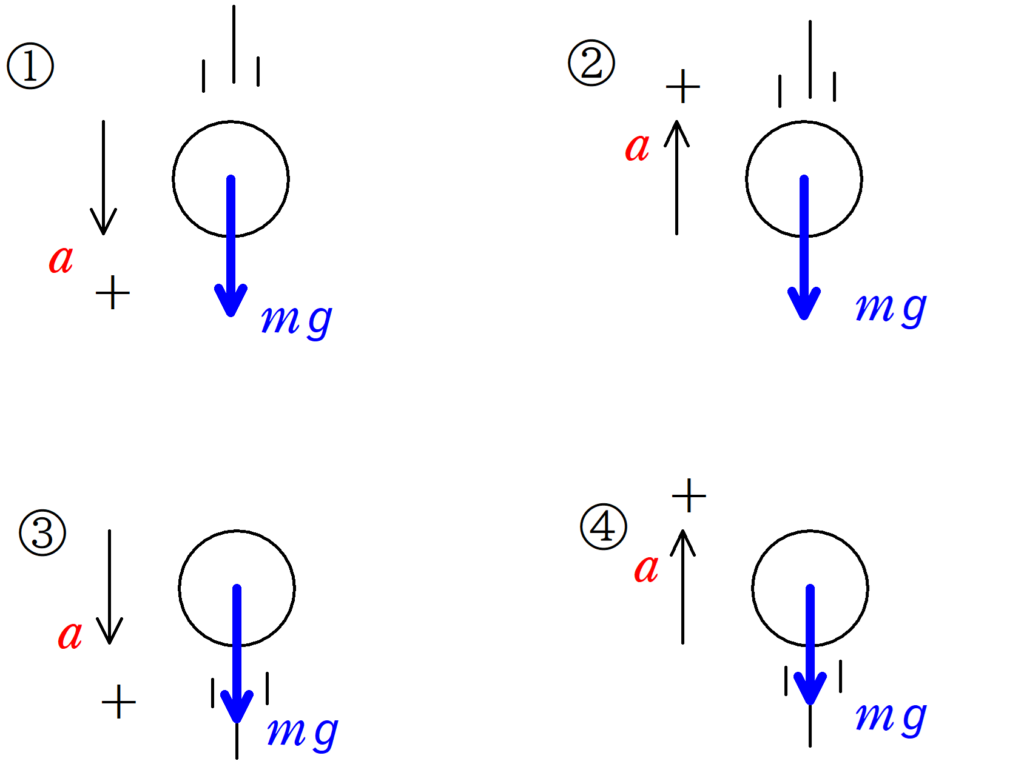

そして,重力の方向と+の方向が同じであれば,$+mg$とし,
重力の方向と+の方向が逆であれば,$-mg$とします.
したがって,それぞれの問いの答えは次のようになります.
(1) 運動方程式を立てて
$ma=mg$ $\therefore a=g$
(2) 運動方程式を立てて
$ma=-mg$ $\therefore a=-g$
(3) 運動方程式を立てて
$a=mg$ $\therefore a=g$
(4) 運動方程式を立てて
$ma=-mg$ $\therefore a=-g$

つまり,物体の動いている向きとは関係なく,加速度は力の向きで決まります.
運動方程式を立てる際には
1. +の向きを決め,その+の向きを加速度の向きとする.
2. 物体の速度の向きとは関係なく,はたらく力をかき,運動方程式を立てる.
3. 力の向きは1.で決めた正の方向であれば,正とし,負の方向に向いていれば負としてかく.

コメント
[…] […]
[…] […]