
U字管の単振動の問題や,ピストンの上に液体がのっている問題では,液体の位置エネルギーの変化を考えているけど,どのように計算すればいいんだろう??

一般的に,大きさがある物体の位置エネルギーは次のように考えることができます.
大きさのある物体の位置エネルギー
重力による位置エネルギーの基準点を$z=0$とし,鉛直上向きに$z$座標をとる.(重力加速度$g$が変化しないくらいのスケールにおいて)重心の$z$座標を$z_{\rm G}$とすると,質量$m$の大きさのある物体の位置エネルギー$U$は,「重心に質量$m$が集中した」と考えてよく,
$U=mgz_{\rm G}$
となる.
※ 正確には,重心座標ではなく基準点からの鉛直距離で,基準点よる上にあれば+,下にあれば-)

なんで,重心に質量が集まったと考えていいんだろう??

★ 2つの物体の場合
質量$m_{1}$の物体の座標が$(x_{1} , y_{1} , z_{1})$,質量$m_{2}$の物体の座標が$(x_{2} , y_{2} , z_{2})$のとき,2つの物体の重心座標$(x_{\rm G},y_{\rm G},z_{\rm G})$は次のようになる.
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$
$y_{\rm G}=\dfrac{m_{1}y_{1}+m_{2}y_{2}}{m_{1}+m_{2}}$
$z_{\rm G}=\dfrac{m_{1}z_{1}+m_{2}z_{2}}{m_{1}+m_{2}}$
★ $n$個の物体の場合
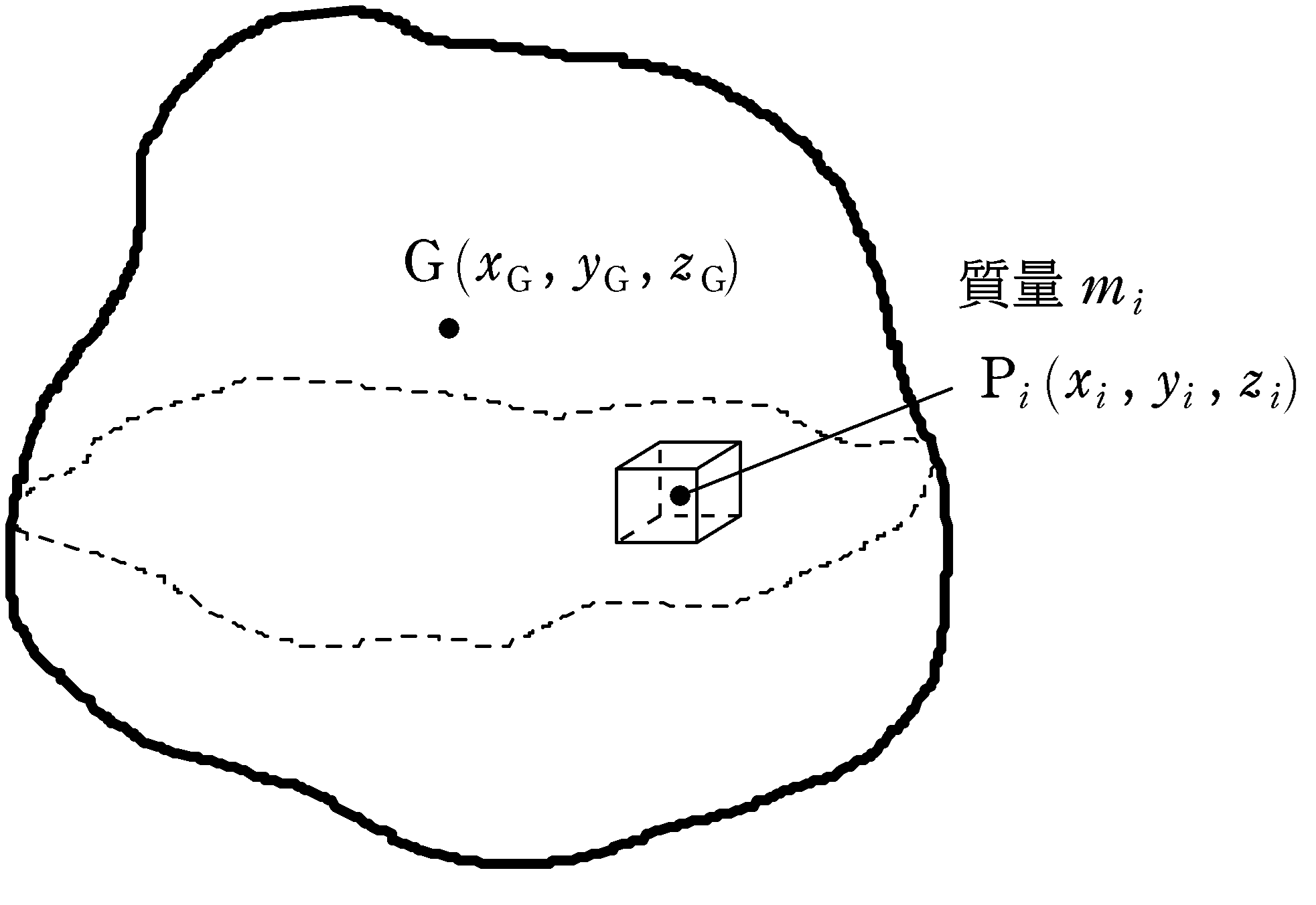
質量$m_{1} , m_{2} , \cdots , m_{n}$の物体の座標をそれぞれ$(x_{1} , y_{1} , z_{1}) $,$(x_{2} , y_{2} , z_{2})$,$\cdots , (x_{n} , y_{n} , z_{n})$とするとき,$n$個の物体の重心座標$(x_{\rm G},y_{\rm G},z_{\rm G})$は次のようになる.
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}+\cdots +m_{n}x_{n}}{m_{1}+m_{2}+\cdots +m_{n}}= \dfrac{ \sum_{i=1}^{n}{m_{i}x_{i}} }{\sum_{i=1}^{n}{m_{i}}} $
$y_{\rm G}=\dfrac{m_{1}y_{1}+m_{2}y_{2} +\cdots +m_{n}y_{n} }{m_{1}+m_{2} +\cdots +m_{n}}= \dfrac{ \sum_{i=1}^{n}{m_{i}y_{i}} }{\sum_{i=1}^{n}{m_{i}}} $
$z_{\rm G}=\dfrac{m_{1}z_{1}+m_{2}z_{2} +\cdots +m_{n}z_{n} }{m_{1}+m_{2} +\cdots +m_{n} }= \displaystyle{\frac{ \sum_{i=1}^{n}{m_{i}z_{i}} }{\sum_{i=1}^{n}{m_{i}}}} $
和の記号を用いると見栄えがよくなります.

上の重心の定義の$z$座標について,次のように変形して次の計算で使います.
$\displaystyle{\sum_{i=1}^{n}{m_{i}z_{i}}=z_{\rm G}\sum_{i=1}^{n}{m_{i}}}$
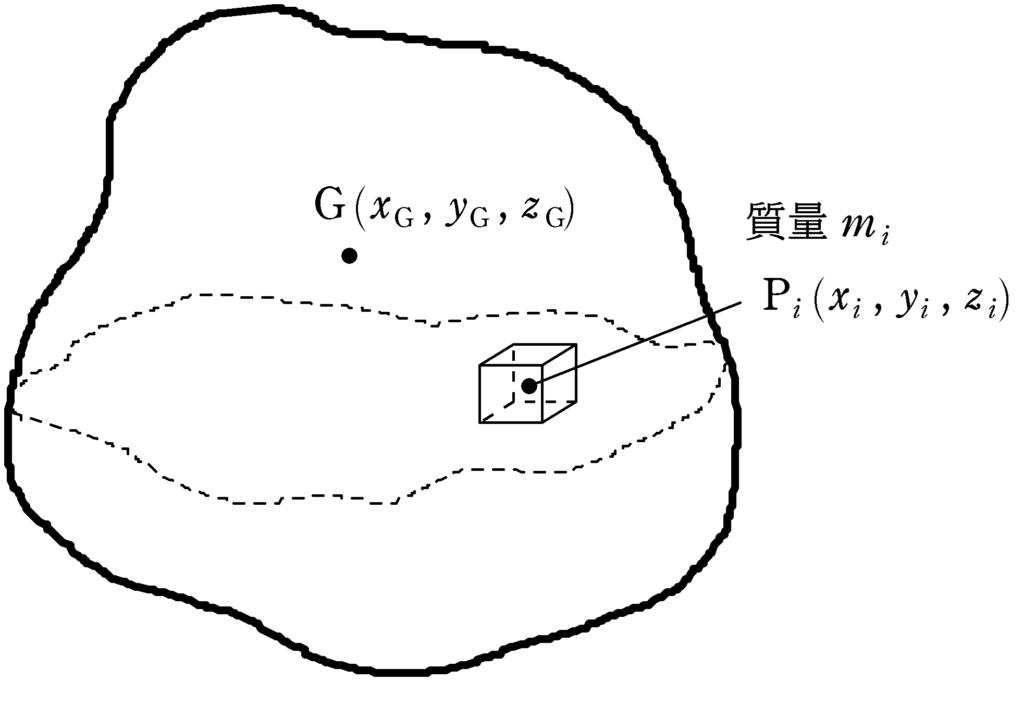

上図のような大きさのある物体を$n$個の物体に分割して,重力による位置エネルギーの和$U$を考えましょう.すると,次のようになります.
ちなみに,重力による位置エネルギーの基準点は$z=0$として,$z$軸の方向が鉛直上方向になるように座標をとっています.
$\eqalign{U&=m_{1}gz_{1}+m_{2}gz_{2}+\cdots +m_{n}gz_{n}\\&=g\sum_{i=1}^{n}{m_{i}z_{i}}\\&=gz_{\rm G}\sum_{i=1}^{n}{m_{i}}}$

なるほど!$\displaystyle{\sum_{i=1}^{n}{m_{i}}}$は$n$個の物体の和だから,これを$M$とすると
$U=Mgz_{\rm G}$
となって,
位置エネルギー=(大きさのある物体の質量)$\times$重心の座標$\times g$
となっているね.(正確には,重心座標ではなく基準点からの鉛直距離で,基準点よる上にあれば+,下にあれば-)
U字管に入っている液体の位置エネルギー変化

これをふまえた上で次の例について考えてみましょう.
下は断面積$S$のU字管に密度$\rho$の液体が入っている図です.
はじめは,左右で同じ高さでしたが,なにかのきっかけで左側が$h$下がり,右側が$h$上がりました.このときの液体の位置エネルギーの変化を考えてみましょう.
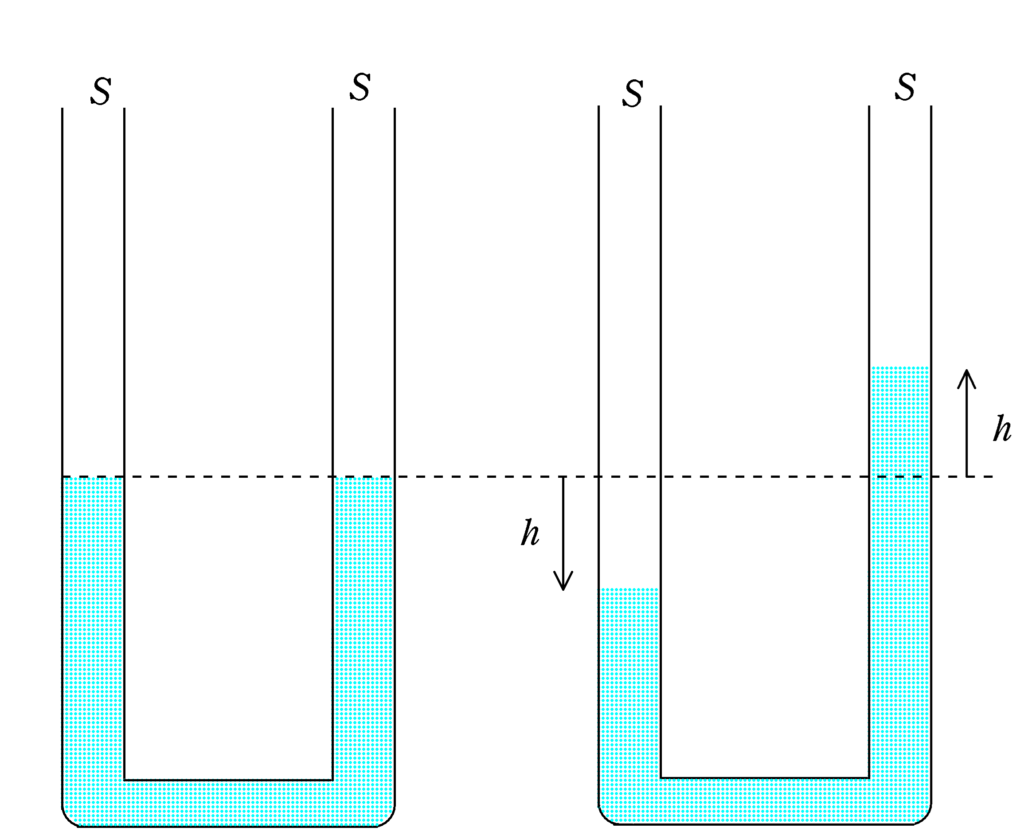

下図の青色部分で囲まれた位置エネルギーの変化を考えればいいのかな?
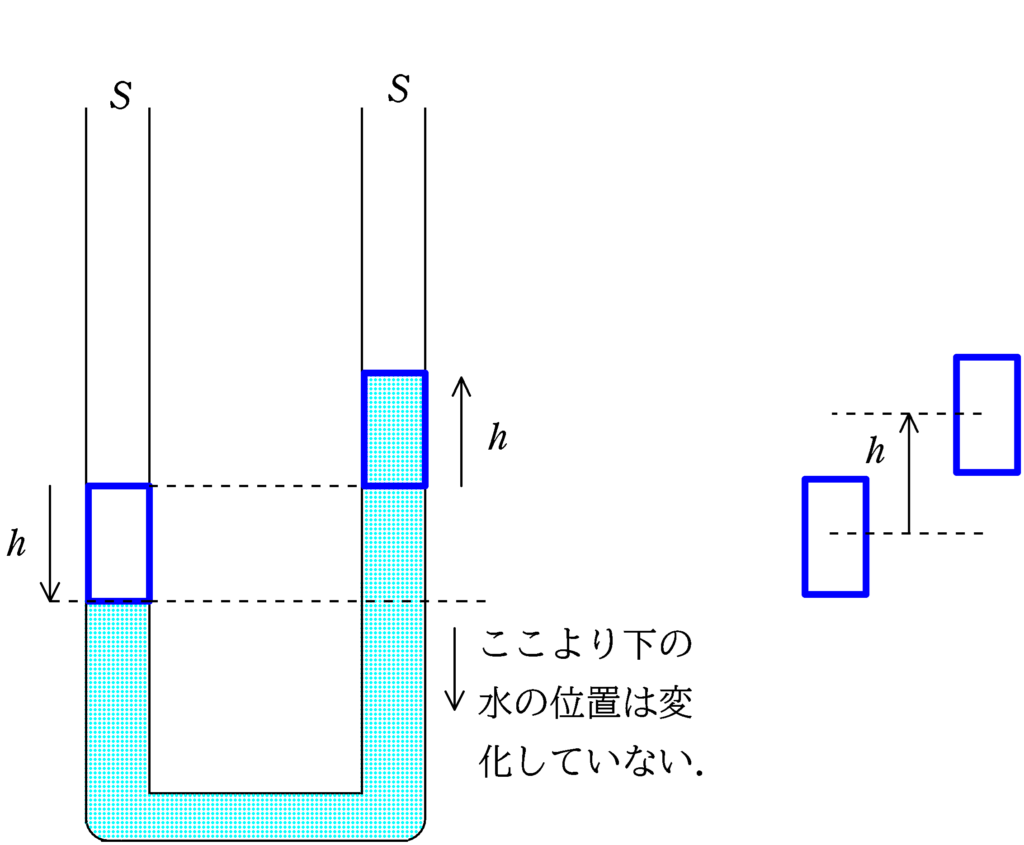

その通りです.
重心は鉛直上向きに$h$だけ移動していて,質量は$\rho Sh$なので,位置エネルギーの変化$\varDelta U$は
$\varDelta U=\rho Sh \cdot g \cdot h=\rho Sh^{2}g$
となります.
$2h$移動した!を思う人がいるので注意してください.あくまで重心の鉛直移動距離を考えます.
ピストンの上にある液体の位置エネルギー変化
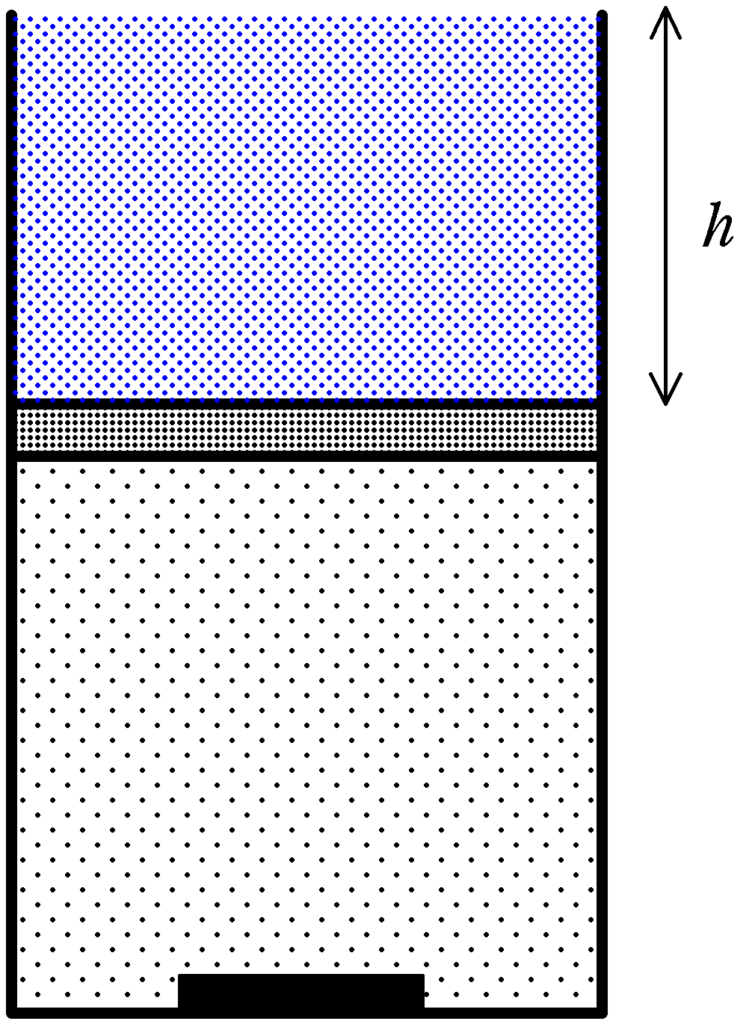

また,熱力学の問題でみられる,ピストンの上に液体があって,容器内の気体を加熱して,少しずつ液体がこぼれる際の液体の位置エネルギー変化を考えていきます.
(液体がこぼれると,位置エネルギーは落ちますが,その分は考えません.あくまで,ピストンがした仕事を考えたいので)

じゃあ,これも重心の位置エネルギー変化を考えればいいんだね.
高さが$h$分の液体だったら,一様な密度の液体の場合,重心は$\dfrac{h}{2}$だけ移動するので,もともとあった液体の質量を$M$とすると
$Mg\cdot \dfrac{h}{2}$
となるんだね.
ただ,今回は液体すべてが移動したというわけではないけどいいのかな.
確かに重心に質量が集まったと考えるのであれば,これであっているんだろうけど..

では,次のように考えてみましょう.
下図のようにピストンから$x\, (0\leqq x\leqq h)$の場所の非常に薄い液体部分がこぼれるまでに変化する位置エネルギーは,液体の密度を$\rho $,厚さを$\varDelta x$,断面積を$S$として,こぼれるまでの距離が$h-x$なので
$\rho S\varDelta x \times (h-x)g$
なります.これをすべて足し合わせます.$\varDelta x\rightarrow dx$として
$\displaystyle{\eqalign{\int_{0}^{x}{ \rho S \times (h-x)g }dx&=\rho S\int_{0}^{h}{(h-x)}dx\\&=\rho S\left[hx-\dfrac{1}{2}x^{2}\right]_{0}^{h}\\&=\dfrac{1}{2}\rho Sh^{2}}}$
ここで,$M=\rho Sh$とおけば,位置エネルギー変化はやはり
$Mg\cdot \dfrac{h}{2}$
となります.
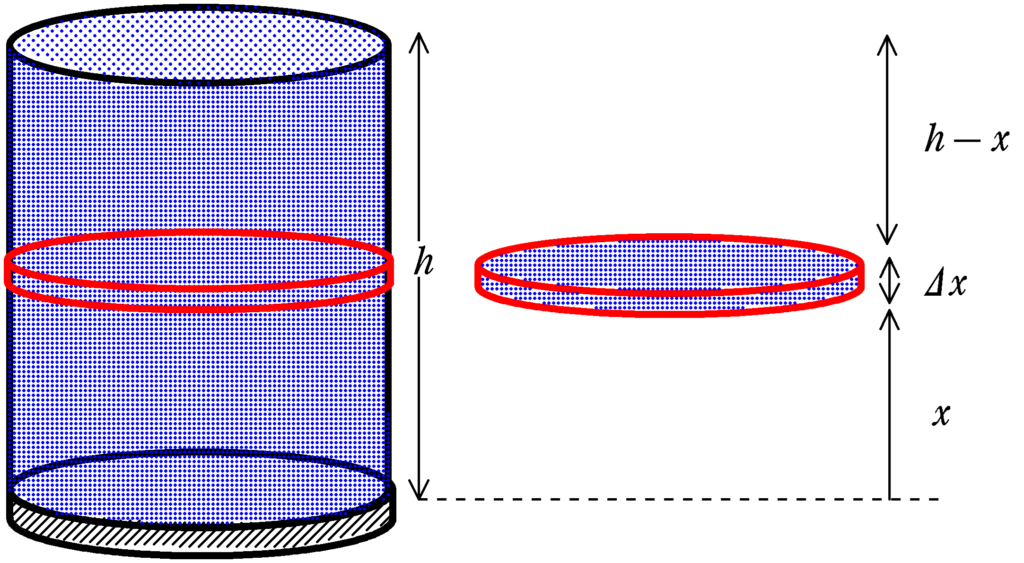

そうか,よく考えたら一番下側にある液体は$h$移動しているけど,上側は移動0だから,平均すると$\dfrac{h}{2}$移動しているんだね!



コメント
[…] 液体の位置エネルギーの変化の計算の仕方 […]