
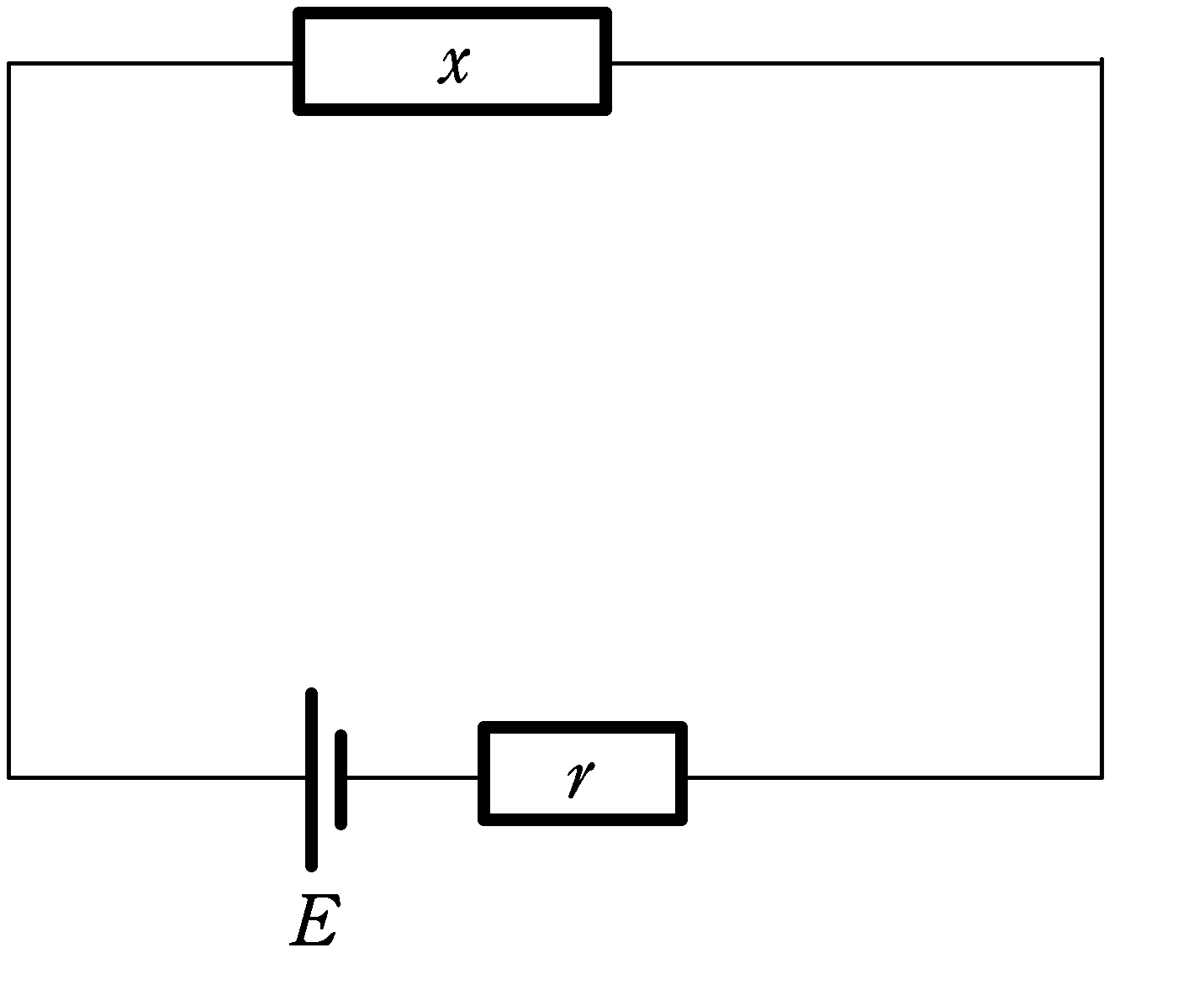
今回は,次図のように,起電力$E$,内部抵抗$r$の直流電池と可変抵抗をつないだとき,可変抵抗での最大消費電力が最大になるときの抵抗値$x$を求めたいと思います.
解法としては
- 相加・相乗平均の不等式の利用
- 2乗の形を作る方法(実質,相加・相乗平均)
- $x$の関数とみて,微分をし,増減表をかく
などがあります.割と基本的な問題では,相加・相乗平均の不等式でうまく計算ができます.
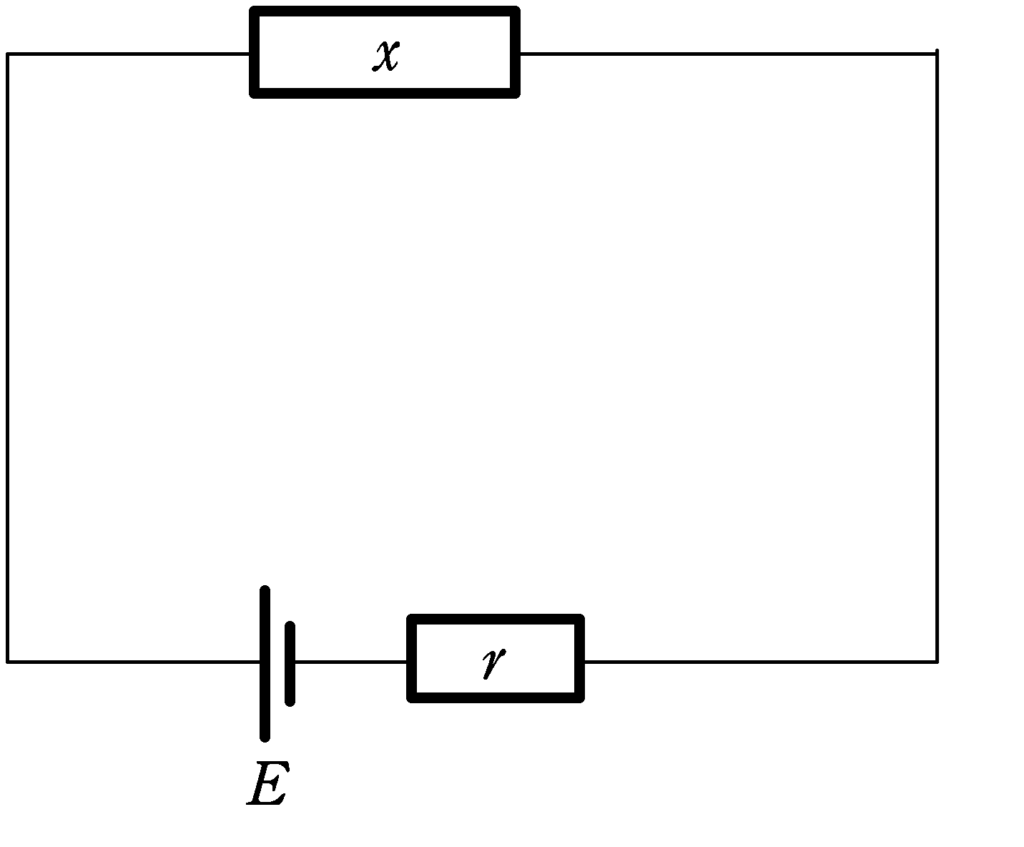

まずは,上に流れる電流を$I$として,キルヒホッフ則を立てましょう.
★ キルヒホッフ則
$E-xI-rI=0$
$\therefore I=\dfrac{E}{x+r}$ $\cdots (\ast)$

オームの法則が成り立つときの抵抗の消費電力$P$は次のように計算できたね.
抵抗に電流$I$が流れたときの抵抗での電圧降下を$V$とする.
このとき,抵抗で単位時間あたりに消費するエネルギー,すなわち消費電力$P$は次のように表される.
$P=IV$
特に,オームの法則が成り立つとき,抵抗を$R$とすると,次のように変形できる.
$P=IV=I^{2}R=\dfrac{V^{2}}{R}$

ここで,可変抵抗で消費する電力を
$EI=E\cdot \dfrac{E}{x+r}$
としてはだめです!
なぜかというと,$E$は可変抵抗にかかる電圧ではなく,可変抵抗と内部抵抗にかかる電圧になっているからです.可変抵抗にかかる電圧は$E-rI$ですが,これは少し面倒なので,
$P=I^{2}x$
を使うことにしましょう.
この回路のように,どの抵抗でも同じ電流が流れているときには,電流$I$を使った消費電力の式の方が使いやすいです.
$(\ast)$より,抵抗$x$の可変抵抗の消費電力$P$は
$P=I^{2}x=\left(\dfrac{E}{x+r}\right)^{2}\cdot x$

$x$を動かしたときの$P$の最大値を求めます.少し形を変形しましょう.
$\eqalign{P&=\dfrac{E^{2}}{(x+r)^{2}}\cdot x\\&=\dfrac{E^{2}x}{x^{2}+2rx+r^{2}}\\&=\dfrac{E^{2}}{x+2r+\dfrac{r^{2}}{x}} \cdots (2\ast)}$

最後の式変形では,分母・分子を$x$で割りました.
これを相加・相乗平均の不等式を使って計算しましょう.
$a\geqq 0,b\geqq 0$の任意の$a , b$について
$(\sqrt{a}-\sqrt{b})\geqq 0$
が成り立つ.これを展開して整理すると
$a+b\geqq 2\sqrt{ab}$
となる.等号が成り立つのは,$\sqrt{a}=\sqrt{b}$すなわち,$a=b$のときである.

$(2\ast)$の分母にある$x+\dfrac{r^{2}}{x}$に着目し,$x\geqq 0$,$\dfrac{r^{2}}{x}\geqq0$なので,相加・相乗平均の不等式を使いましょう.
★ 相加・相乗平均の不等式
$x+\dfrac{r^{2}}{x}\geqq 2\sqrt{\cancel{x}\cdot \dfrac{r^{2}}{\cancel{x}}}=2r$ $\cdots (3\ast)$

さらに,$(2\ast)$の分母の形をつくるために,上式の両辺に$2r$を足します.
$x+\dfrac{r^{2}}{x}+2r\geqq 2r+2r=4r$

さらに,$(2\ast)$の形をつくるために逆数をとります.両辺とも正の数なので,逆数をとると不等号の向きが逆になるね.
$\dfrac{1}{x+\dfrac{r^{2}}{x}+2r}\leqq \dfrac{1}{4r}$

さらに,両辺$E^{2}$をかけて,$(2\ast)$の形をつくりましょう.
$\dfrac{E^{2}}{x+\dfrac{r^{2}}{x}+2r}\leqq \dfrac{E^{2}}{4r}$

$(3\ast)$の不等式からスタートしたので,等号成立は
$x=\dfrac{r^{2}}{x}$
すなわち,$x=r$のときだね.このとき,消費電力の最大値は$\dfrac{E^{2}}{4r}$をとります.

また,$(2\ast)$を次のように変形してもよいです.
$P= \dfrac{E^{2}}{x+2r+\dfrac{r^{2}}{x}}=\dfrac{E^{2}}{\left(\sqrt{x}-\dfrac{r}{\sqrt{x}}\right)^{2}+4r}$
このように変形すると,$( )^{2}$の中が0のとき,分母が最小となり,$P$が最小となることがわかります.
また,$f(x)= \dfrac{E^{2}}{x+2r+\dfrac{r^{2}}{x}} $を微分して増減表をかくことで最大値を調べることもできます.


コメント