物理のエッセンス解説　熱-12

物理のエッセンスでよく質問される問題を解説します．

問題文は物理のエッセンスを読んでください．

この問題で一番質問されるのが，

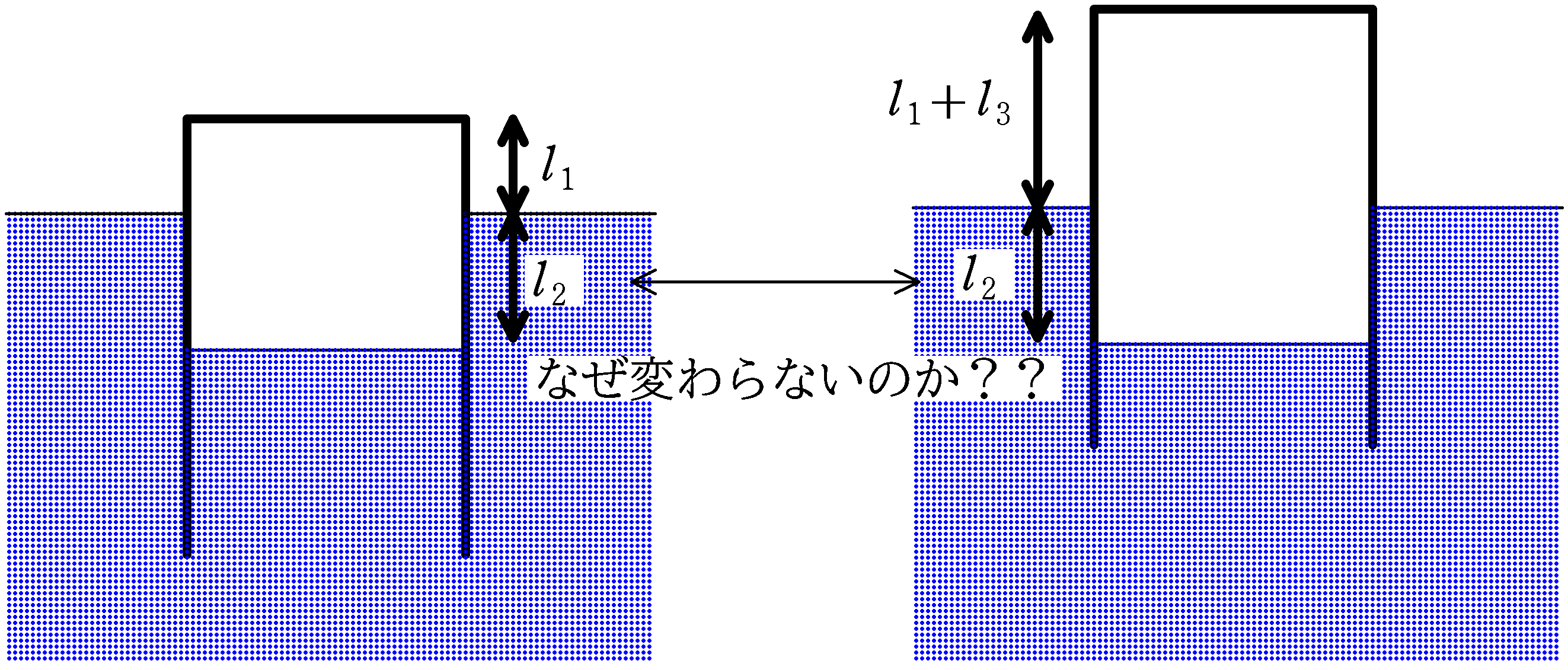
「なぜ，筒外の水面と筒内の水面の差が$l_{2}$のままなのか？」

ということです．

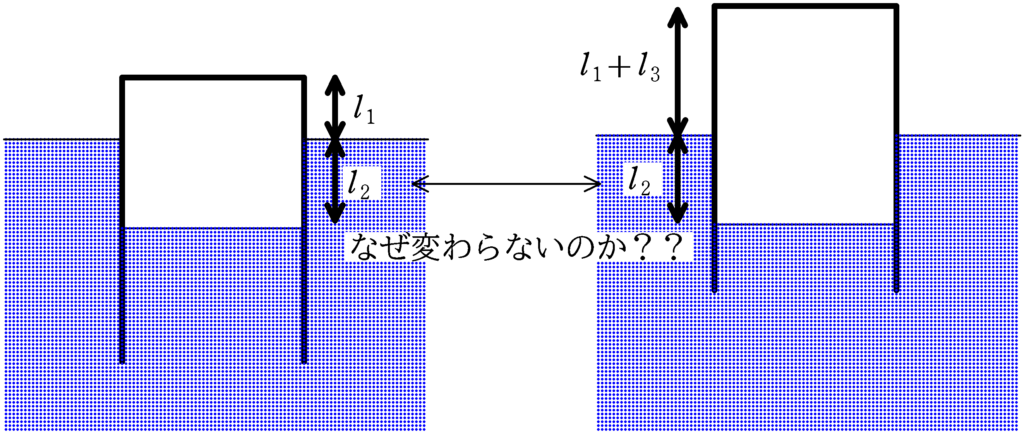
この問題を考える際に，熱力学の問題で立てる3つの式を確認しましょう．

今回キーとなるのは，可動部分（というかつり合いを考える部分）が2箇所あるということです．

それは，

• 筒
• 筒内の水面

です．

それぞれにはたらく力を考えてみましょう．

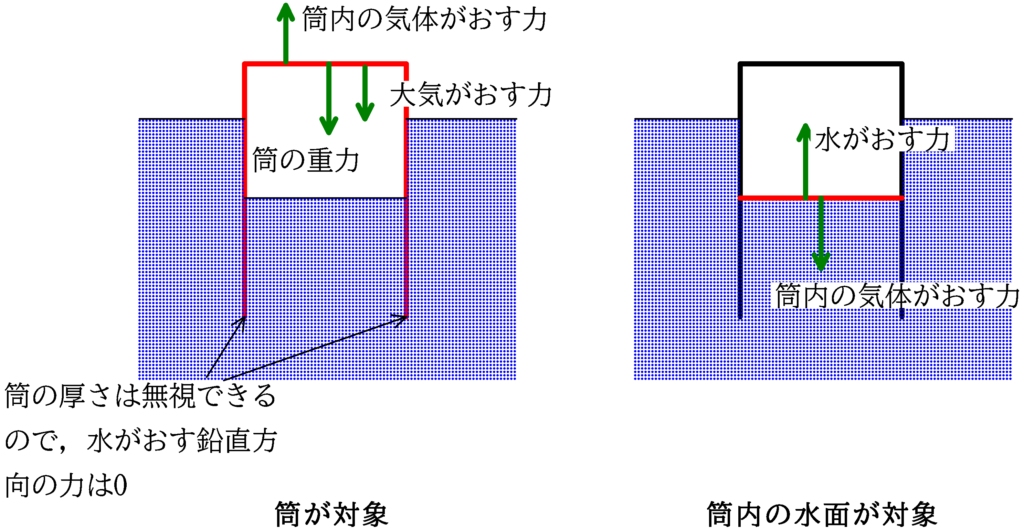
筒自体にはたらく力（鉛直方向のみです．）は，「筒の重力」と「大気がおす力」と「筒内の気体がおす力」です．

このうち，たとえ筒内の気体を加熱しても「筒の重力」と「大気がおす力」は変化しません．

すると力のつり合いを考えれば，「筒内の気体がおす力」も変化しません．

つまり，筒を対象とした力のつり合いを考えることで，定圧変化であることがわかるわけです．

一方，筒内の水面にはたらく力は「筒内の気体がおす力」と「水がおす力」の2つです．

このうち，「筒内の圧力」は（筒内の空気の重さを考えないと仮定していると思うので，筒内部の上側をおす圧力も水面をおす圧力も同じはずです．）変化しないので，水面にはたらく力のつり合いを考えると，「水がおす力」も変化しません．

ところで，水圧は水の深さで決まります．（こちらを参照してください．

したがって，筒内の水圧が変化しないので，筒内の水面の深さは変化しません．

定圧変化なので，筒内の気体の圧力さえわかれば，A（筒内の気体）がした仕事は簡単に計算できます．

この問題では，筒自体の質量が与えられていないので，筒内の水面のつり合いを考えることで筒内の気体の圧力$P$を求めてみましょう．

水圧は次のステップで求めます．

1. 知りたい水圧$P$と同じ深さの圧力のつり合いを考える．
2. 深さが同じ場所では同じ水圧であることを利用して$P$を求める．

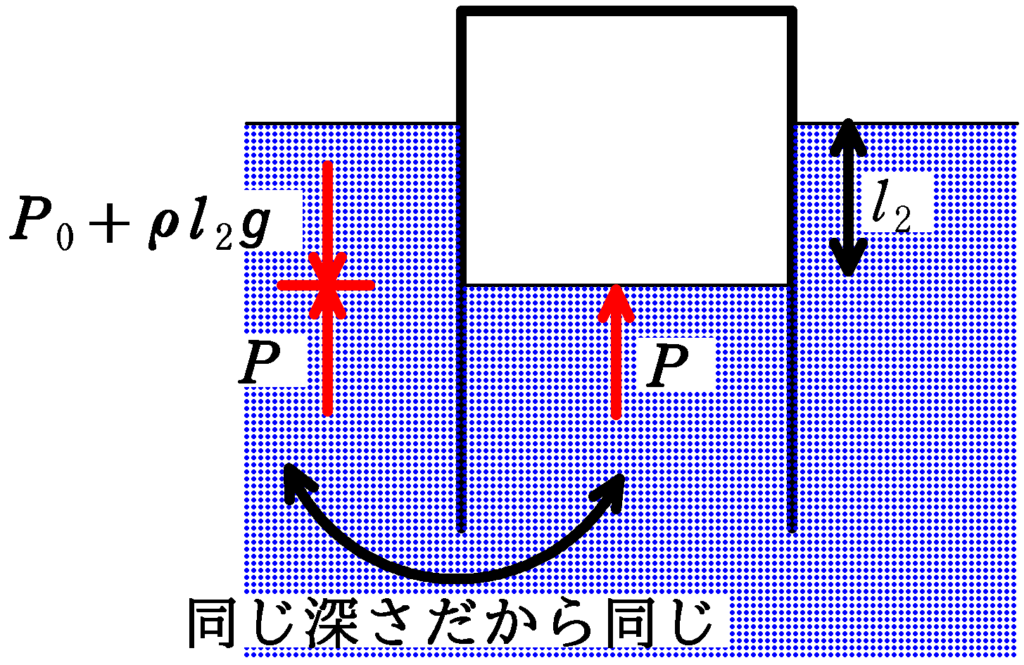
深さ$l_{2}$の圧力は大気圧$P_{0}$を合わせて

$P_{0}+\rho l_{2}g$

となります．したがって，水圧は

$P=P_{0}+\rho l_{2}g$

であり，筒内の水面のつり合いを考えれば，筒内の気体の圧力も$P=P_{0}+\rho l_{2}g$　(答)とわかります．

定圧変化なので，気体の体積変化を$\varDelta V$とすると，$W=P\varDelta V$です．

$\varDelta V=Sl_{3}$(問題文に筒内の気体の縦の長さが$l_{1}+l_{2}\to l_{1}+l_{2}+l_{3}$になると書いてある．)なので

$W=PSl_{3}=(P_{0}+\rho l_{2}g)Sl_{3}$　(答)