
図の右方向に加速している電車内において,ヘリウムを入れた膜部分の質量が無視できる風船をかるいひもにつないで,下端を電車の床に固定しておきます.すると,風船は左と右どちらに傾くと思いますか?
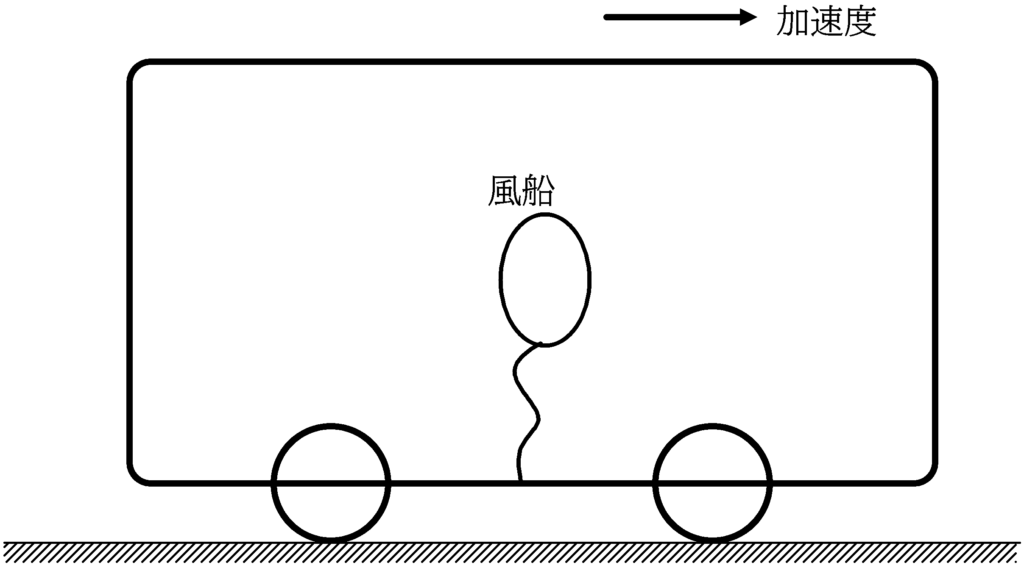

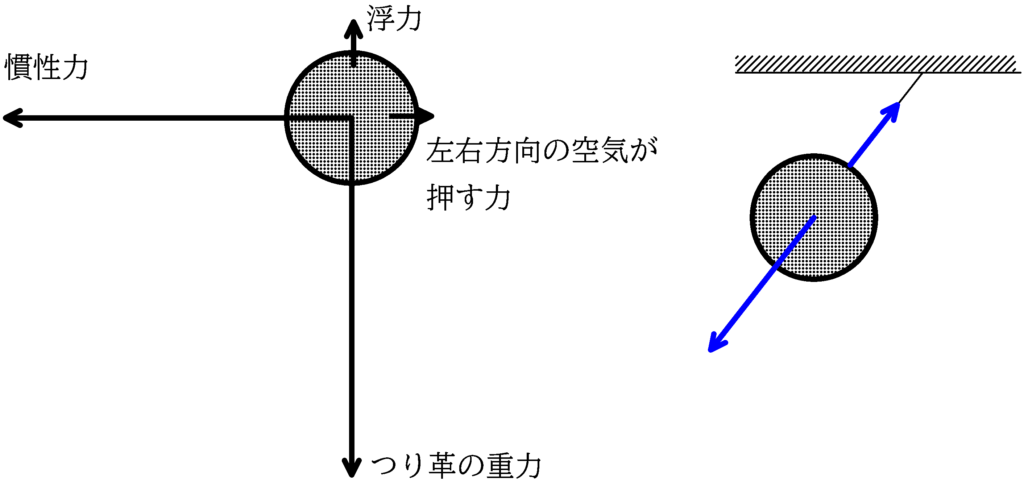
電車のつり革は加速度運動している方向と反対方向と逆方向に慣性力を受けて(電車内から見たた場合)左方向に移動するんだから,風船も同じく左に移動するんじゃない??

いえ,実は風船は右に移動するんです.

へー,不思議!!
なんでなんだろう??

それでは,風船にはたらく力を考えてみましょう.
その前に,電車内の空気は電車内で静止しているとしましょう.すると,電車とともに加速度運動していることになります.
下図のような,密度が$\rho_{空気}$,長さが$a , b , c$である直方体の空気にはたらく力を考えます.
電車(および空気)の加速度を$\beta$とし,空気のカタマリの左からの圧力を$P_{1}$,右からの圧力を$P_{2}$,上からの圧力を$P_{3}$,下からの圧力を$P_{4}$,重力加速度の大きさを$g$とします.
この空気のカタマリの水平方向の運動方程式と鉛直方向のつり合いの式を立てましょう.
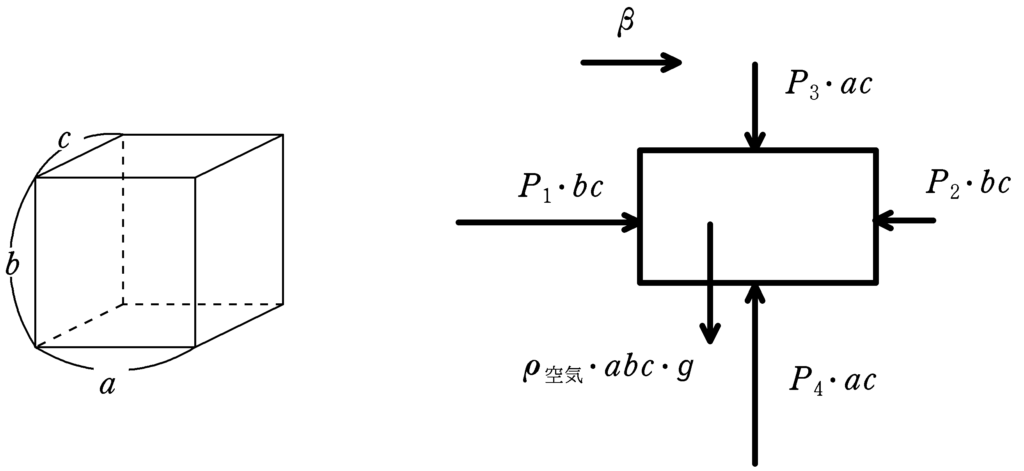
★ 水平方向の運動方程式
$\rho_{空気}abc\cdot \beta=P_{1}bc-P_{2}bc$ $\cdots (\ast)$
★ 鉛直方向のつり合い
$P_{3}ac+\rho_{空気}abc\cdot g=P_{4}ac$ $\cdots (2\ast)$

$(\ast)$によれば,左右の圧力差は右向きに
$P_{1}-P_{2}=\rho_{空気}a\beta$ $\cdots (3\ast)$
つまり,空気が左右から押される単位面積あたりの力は,空気の密度と左右方向の長さと電車の加速度が関係しているんだね.
また,$(2\ast)$によれば,上下方向の圧力差は上方向に
$P_{4}-P_{3}=\rho_{空気}bg$ $\cdots (4\ast)$
つまり,空気が上下から押される単位面積あたりの力は,空気の密度と,上下方向の長さと重力加速度が関係してくるんだね.

$(4\ast)$の上下の圧力差により受ける力が浮力でしたね.
浮力については下の記事でも説明しています.
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.

$(3\ast)$は,電車の中からみると,左右方向にもこの浮力みたいなものがはたらくと考えることができるんじゃない??

その通りです.
ヘリウムの密度を$\rho_{ヘリウム}$として,電車の中からみた風船にはたらく力を考えてみましょう.とりあえずはじめ張力は考えないものとします.
風船の体積を$V$としましょう.
風船にはたらく力はどんなものがありますか?

右方向に左右の圧力差により生じる力(浮力の左右バージョン),$\rho_{空気}V\beta$
左方向に慣性力,$\rho_{ヘリウム}V\beta$
上方向に上下の圧力差による生じる力(浮力),$\rho_{空気}Vg$
下方向にヘリウムの重力,$\rho_{ヘリウム}Vg$
だね.
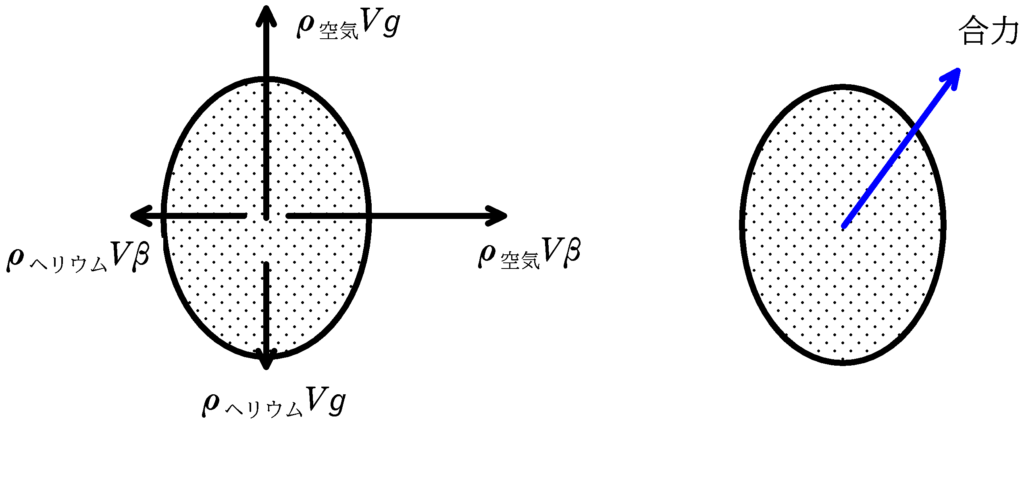

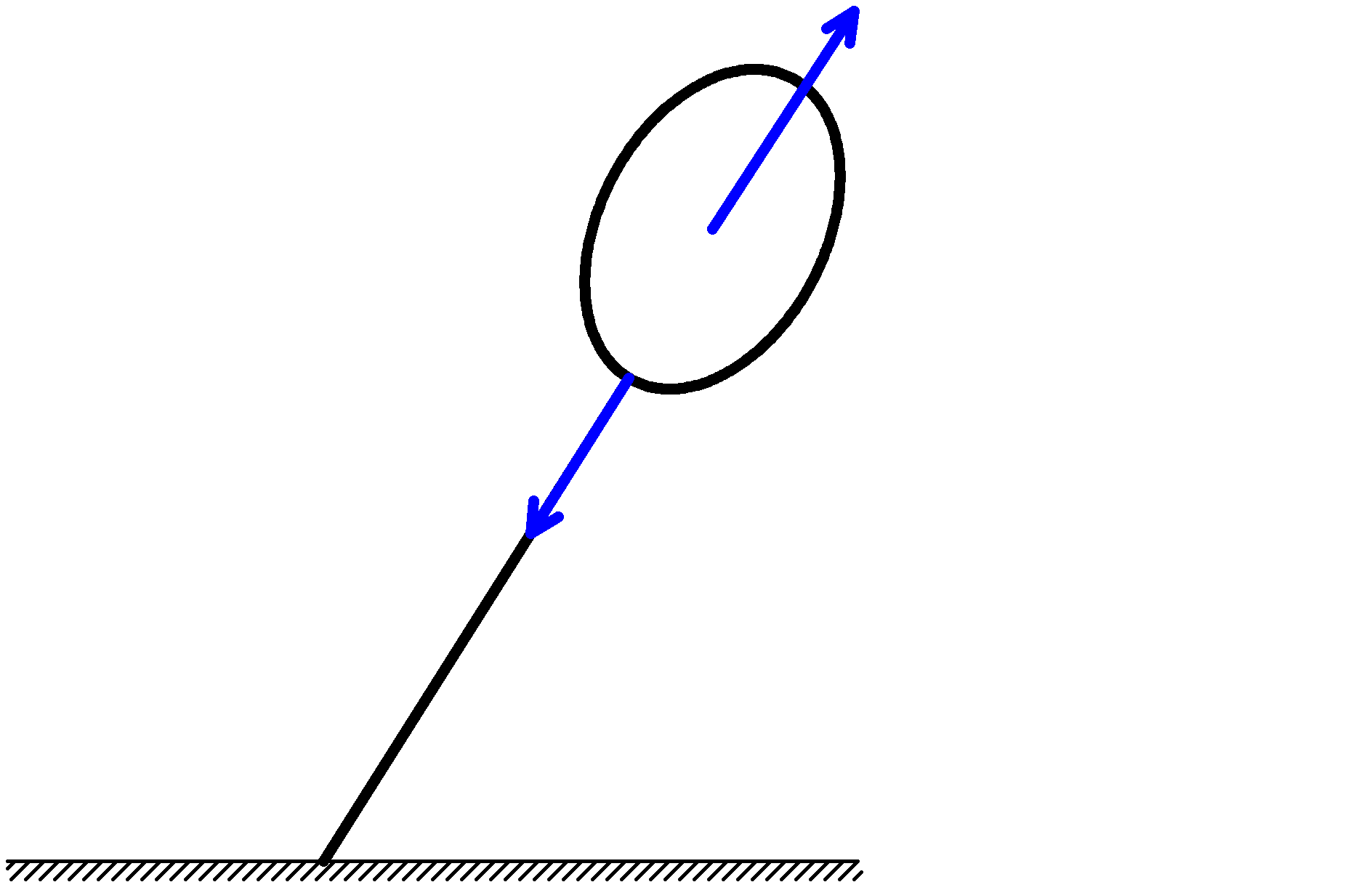
$\rho_{ヘリウム}<\rho_{空気}$なので,上図のように合力は斜め右上になりますね.
その結果,下図のように風船は右に傾くわけです.
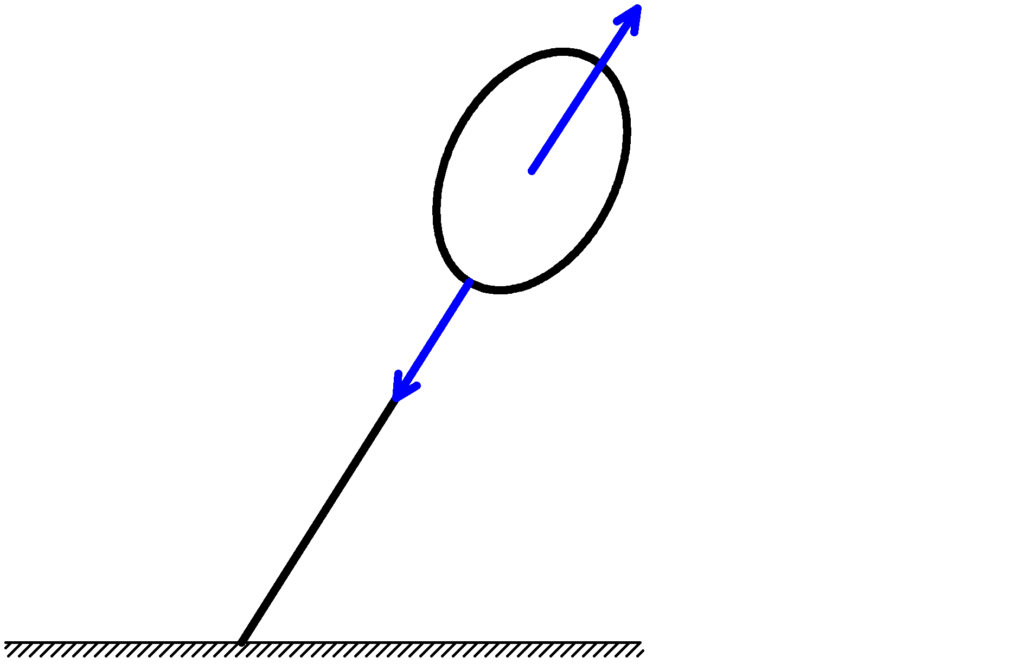

つり革が左に移動するのは,つり革の慣性力と重力が空気が押す力に比べて非常に大きいからなんだね!

そういうことです.

コメント