分流器 | Physicmath（フィジクマス）

PHYさん

電流計と並列にある抵抗を接続することで，電流計の1目盛り（または，最大目盛り）を変えることができます．

NEKO

電流計って，抵抗と直列に接続するんじゃなかったっけ？？

PHYさん

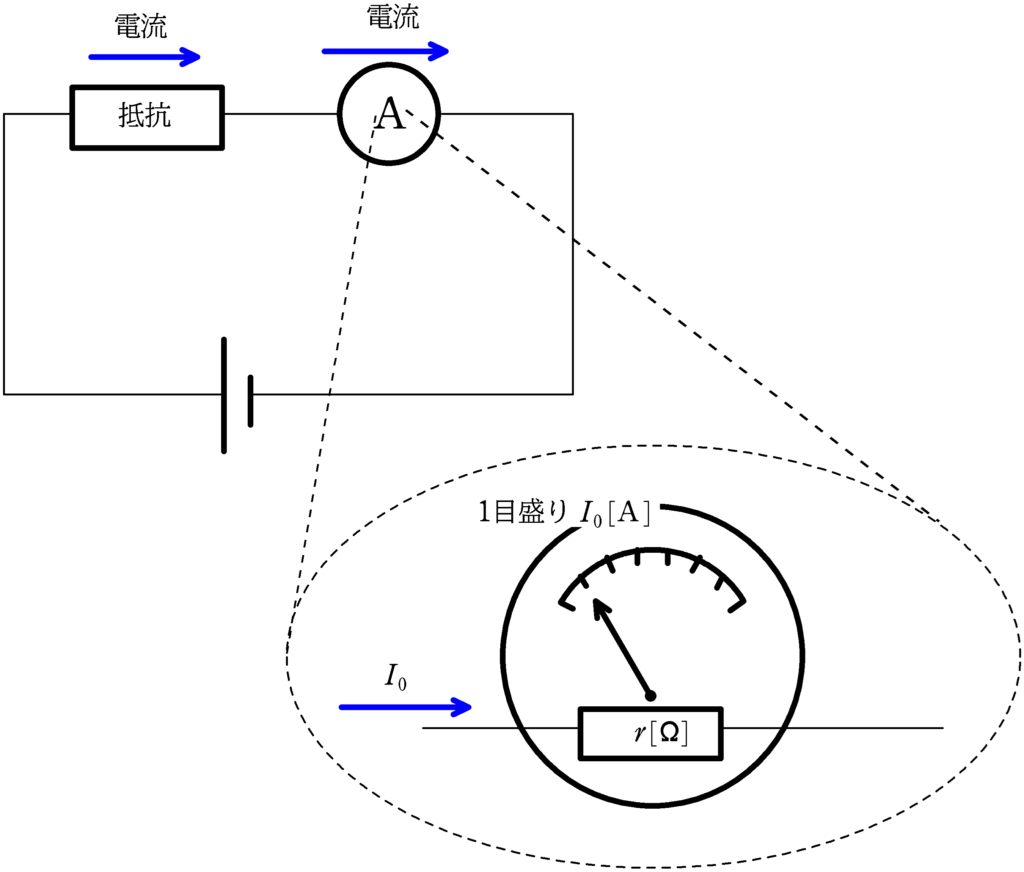
測定したい抵抗（など）と直列に接続するのは正しいです．でも，今は，電流計の内部の話をしているんです．

そもそも，電流計の簡単な仕組みを知っておいた方がよいです．

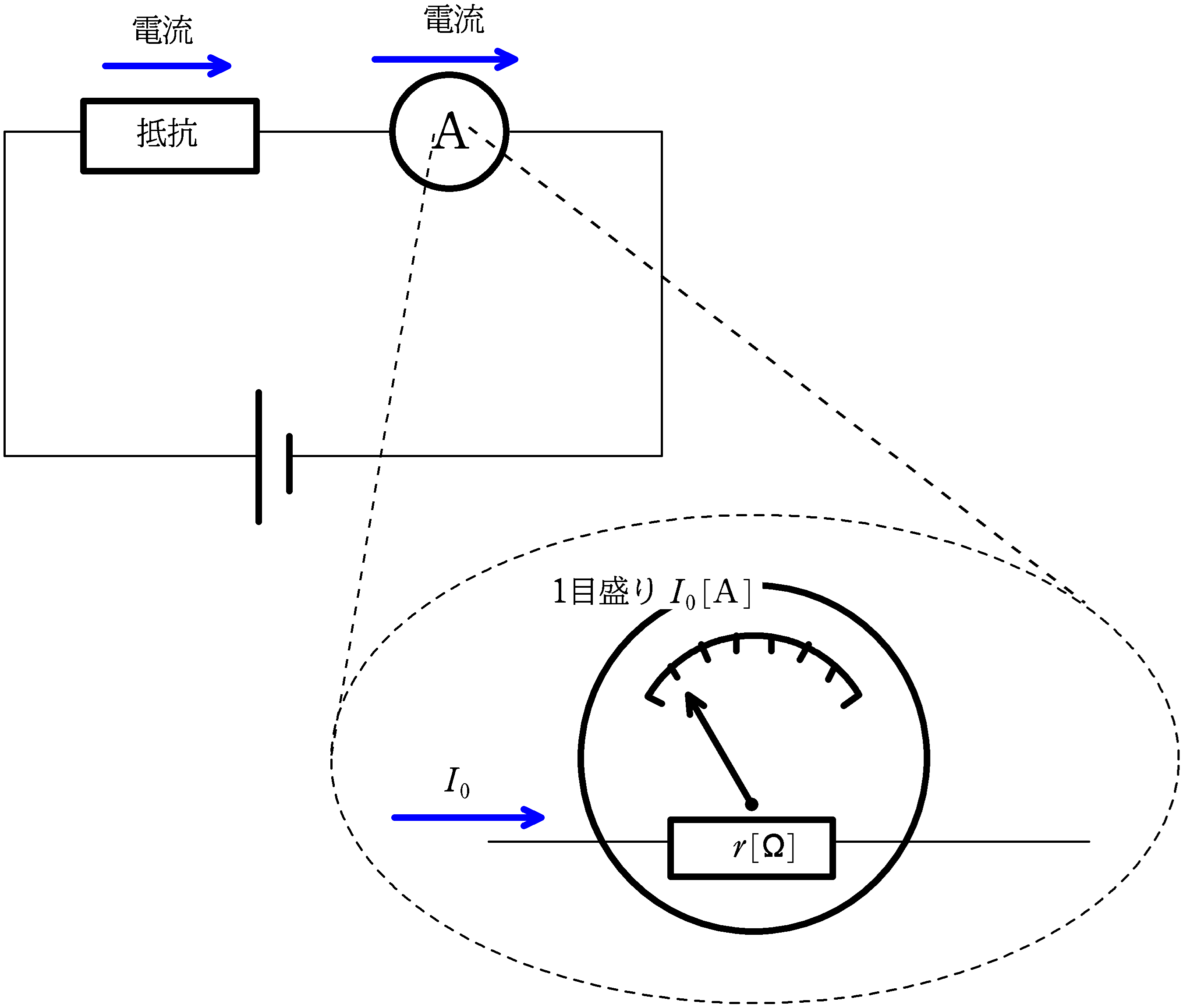
電流計の中には，コイル，渦巻きばね，磁石，針などがあります．

磁石の中にコイルがあり，電流が流れることで電磁力を受け，ばねを通して針が振れます．

そのときの「針の振れは電流の大きさに比例して大きくなることで電流の大きさを測る」わけです．

1目盛り分の針が動く電流の大きさは決まっているので，電流を電流計部分（コイルがあるところ．（上図の$r\,[\Omega]$の抵抗部分）以外のところに流してしまう（分流）ことで，目盛りを変えてしまうんです．

NEKO

例えば，もともと1目盛りが$I_{0}\,[\rm A]$だったものを$x$倍の$xI_{0}\,[\rm A]$にするには，下図のように，電流計部分に$I_{0}\,[\rm A]$流して，残りの

$xI_{0}-I_{0}=(x-1)I_{0}\,[\rm A]$

を分流してしまうということ？？

PHYさん

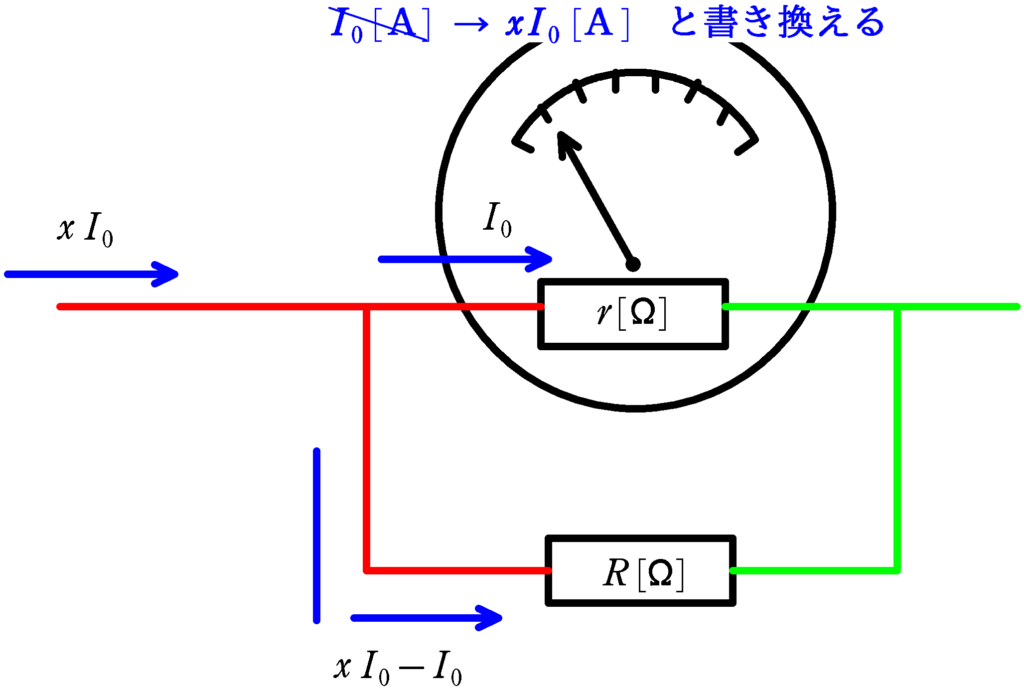
そういうことです．

本当は，コイルには$I_{0}\,[\rm A]$しか流れていないのですが，上図の分流した方も合わせて新たな電流計とすると，電流計の外は$xI_{0}\,[\rm A]$の電流が流れていることになります．

このとき，分流するために抵抗を並列につなぐわけですが，その抵抗値をきかれることがあります．

この抵抗を分流器といいます．分流器の抵抗を$R\,[\Omega]$として，$R$を求めてみましょう．

★　抵抗$r\, [\Omega]$と抵抗$R\,[\Omega]$の電圧が等しいことから

$r\cancel{I_{0}}=R\cdot (x-1)\cancel{I_{0}}$

$\therefore　R=\dfrac{r}{x-1}$

分流器

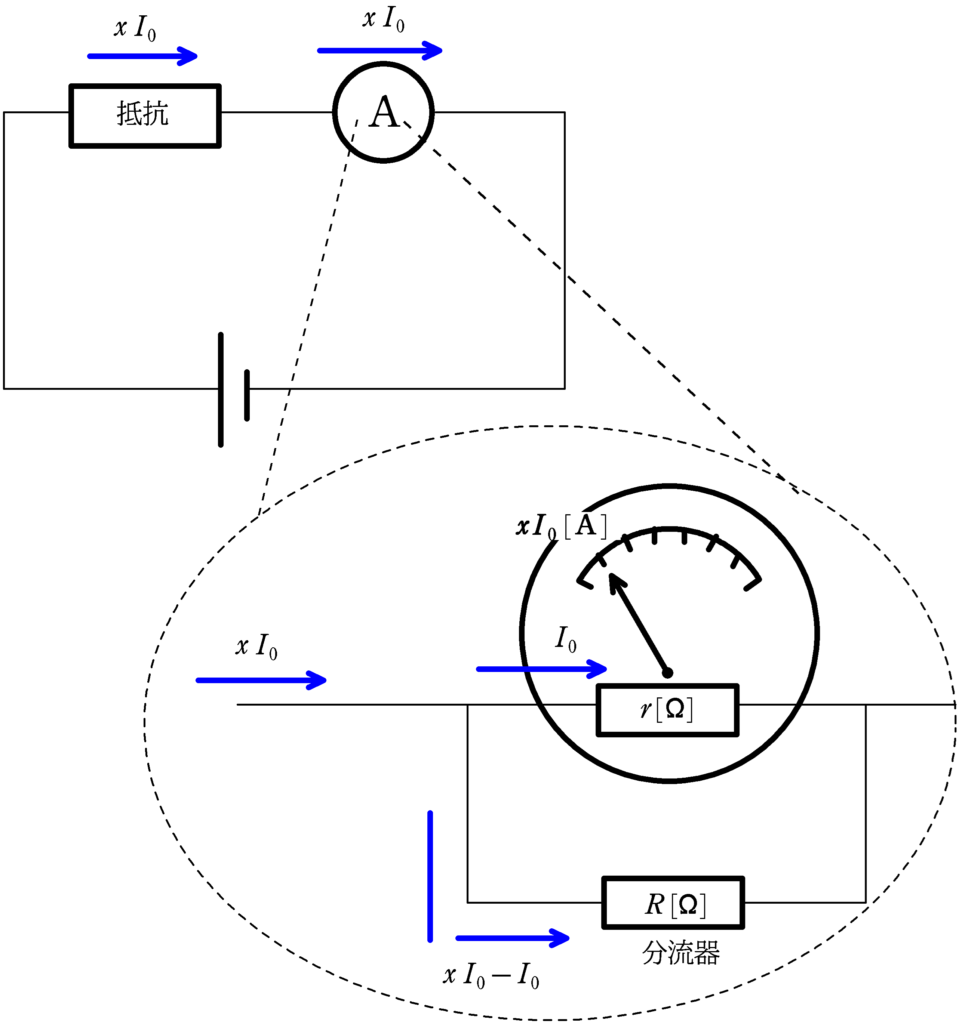
電流計の1目盛り（または，最大目盛り）を元の$x$倍にしたいとき，分流器を検流計（コイルやつるばねがある方上図では抵抗$r\,[\Omega]$ ）に並列につなぐことで，電流を分ける．

分流器の抵抗を問う問題が多い．このとき，答えを覚えておくのではなく，次のステップで考えるとよい．

①　上図のように，1目盛りにしたい電流（または，最大電流），検流計（コイルやばねがある方．上図では抵抗$r\,[\Omega]$），分流器に流す電流を書き込む．その際，キルヒホッフ第1法則を使う．

②　分流器の抵抗を$R\,[\Omega]$と設定し，$r\,[\Omega]$にかかる電圧と$R\,[\Omega]$にかかる電圧が等しいことを利用して$R\,[\Omega]$を求める．

※　参考に

　1目盛り（最大目盛り）を$x$にしたいとき，分流器は検流計（コイルやばねがある方）と並列につなぎ，その抵抗は

$R= \dfrac{r}{x-1} $

とすればよい．

NEKO

図をかけば，そこまで難しくなさそうだね．

演習問題をやってみよう．

問題

1目盛りが$1\,{\rm mA}$で内部抵抗が$1\,\Omega$の電流計がある．この電流計の1目盛りを$5\,{\rm mA}$にするためには，何$\Omega$の抵抗をどのように（直列または並列）に接続すればよいか．

<解答>

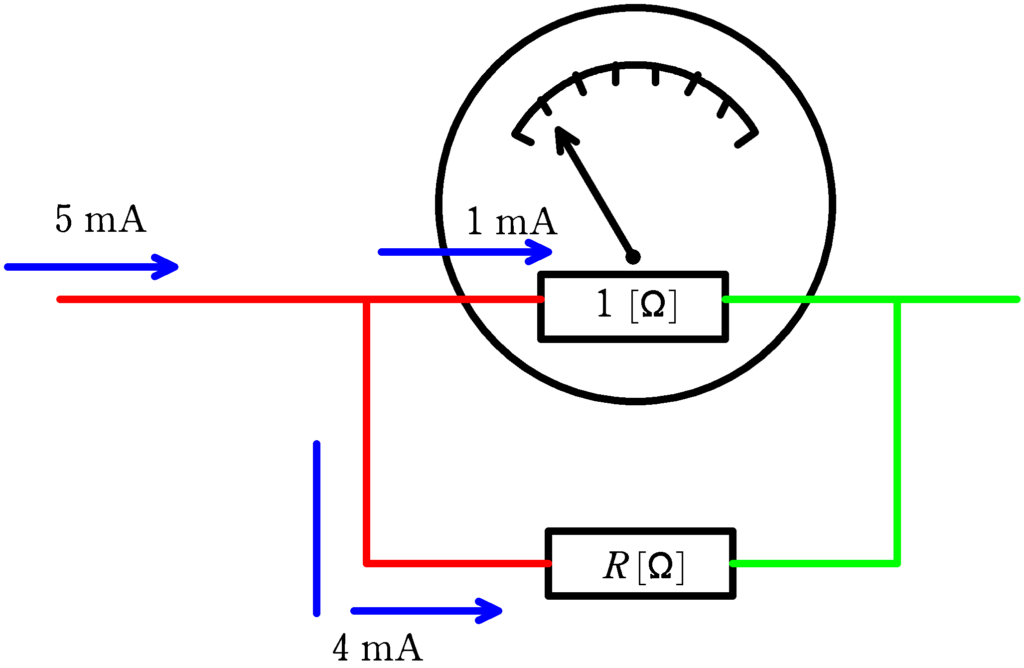
上図のように，分流器は$1\,[\Omega]$の抵抗と並列(答)につなぐ．その抵抗を$R\,[\Omega]$とする．

$1\,\Omega$の抵抗には$1\,\rm A$を流し，$4\,\rm mA$を分流器に流すことで，1目盛りを$5\,\rm mA$にする．$1\,\Omega$の抵抗と$R\,[\Omega]$の抵抗にかかる電圧が等しいことから

$1\cdot 1\times \cancel{10^{3}}=R\cdot 4\times \cancel{10^{-3}} $

$\therefore R=0.25\, \Omega$　(答)