[演習]束縛条件1 | Physicmath（フィジクマス）

NEKO

このシリーズでは，「束縛条件」を立てる練習をしていきましょう．

基本は「束縛条件」なので，束縛条件に必要な物理量を運動方程式や保存則を立てることはありません．

問題

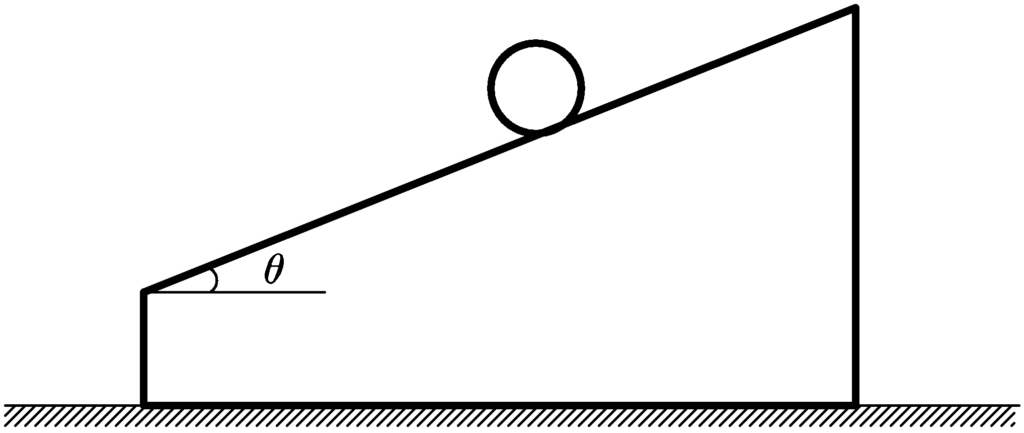
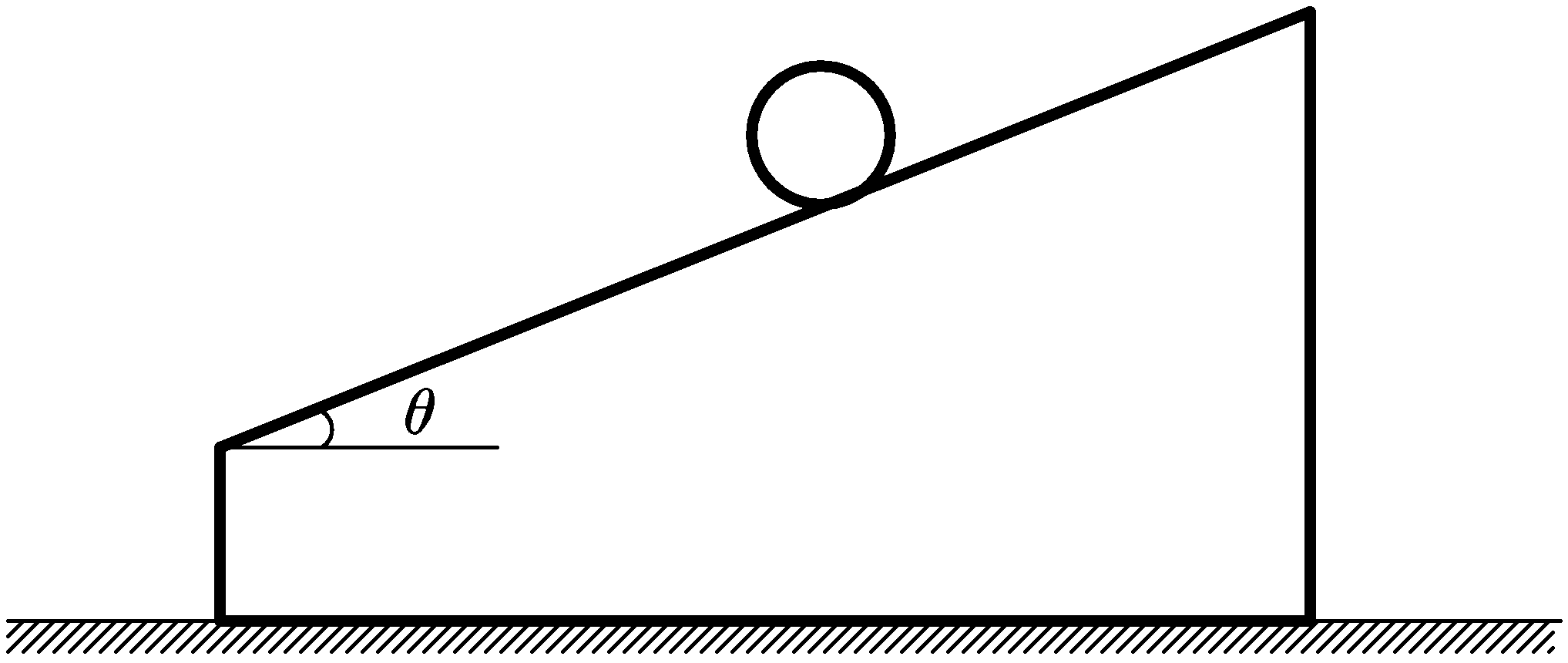
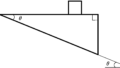
水平でなめらかな床の上に上面に角度$\theta$の斜面をもつ台があり，斜面に物体をおいて手をはなしたところ，物体は斜面上をはなれずに運動した．

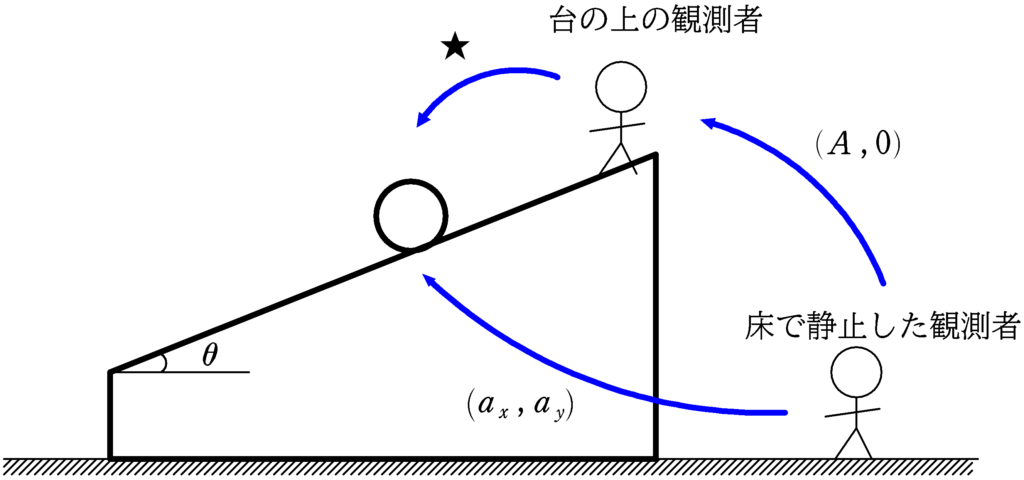
床で静止した観測者からみた水平方向（図の左方向を正）の加速度を$a_{x}$，鉛直方向（鉛直下方向を正）の加速度を$a_{y}$とする．

また，台車の水平方向(左方向を正)の加速度を$A$とする．

物体が斜面を離れないという束縛条件から，$a_{x} , a_{y} , A , \theta$の間に成り立つ関係を求めよ．

<解答>

NEKO

「斜面から離れない」ということは，斜面からみた物体の加速度が斜面に平行な方向であるということです．

なので，斜面からみた加速度を求めましょう．

相対加速度は次のような図をかくとよいでしょう．

(加速度の水平成分，加速度の鉛直成分)で表し，次の式を

を立て，(加速度の水平成分，加速度の鉛直成分)で表し，次の式を立てましょう．

$(A , 0)+$★$＝(a_{x} , a_{y})$

$\therefore ★=(a_{x}-A , a_{y})$

NEKO

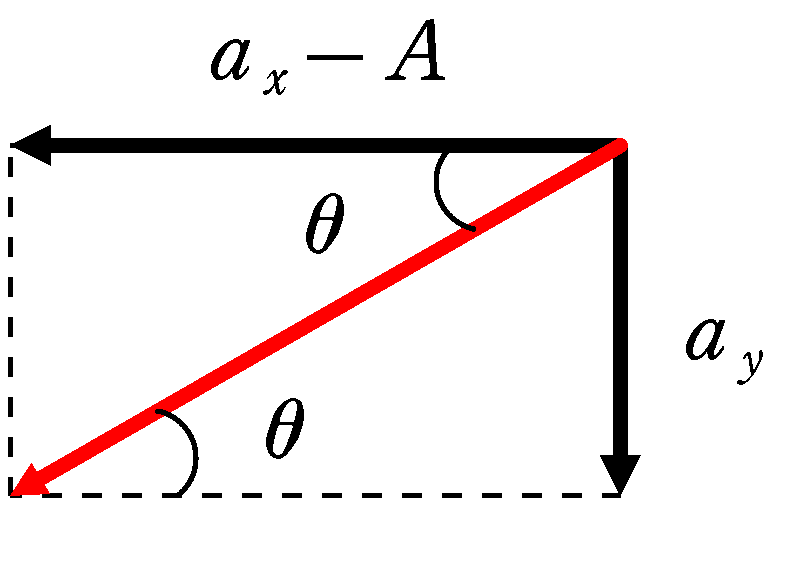
つまり，斜面からみた水平成分が$a_{x}-A$，鉛直成分が$a_{y}$となります．

NEKO

すると，上図より，$a_{x} , a_{y} , A , \theta$は次のような関係になります．

$\tan\theta=\dfrac{a_{y}}{a_{x}-A}$　(答)