
今回はこちらで扱った問題の別解です.
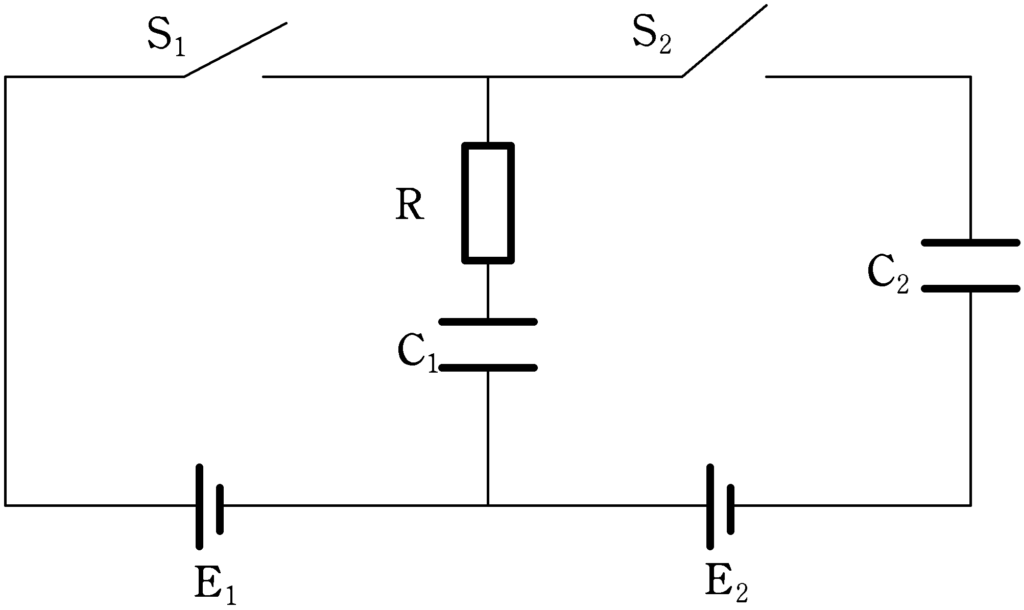
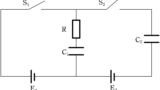
図のように,電圧$V_{0}[\rm V]$,$2V_{0}[\rm V]$の電池$\rm E_{1}$ , $E_{2}$,電気容量がいずれも$C[\rm F]$のコンデンサー$\rm C_{1}$,$\rm C_{2}$,抵抗値$R[\rm \Omega]$の抵抗R,スイッチ$\rm S_{1}$,$\rm S_{2}$が接続されている.最初,スイッチ$\rm S_{1}$,$\rm S_{2}$は開いていて,$\rm C_{1}$,$\rm C_{2}$には電荷が蓄えられていなかった.
はじめの状態から,$\rm S_{1}$を閉じて十分時間が経った後,$\rm S_{1}$を開き,$\rm S_{2}$を閉じた.その後十分時間が経った後,$\rm S_{2}$を開いて,$\rm S_{1}$を閉じた.さらに,十分時間が経った後に$\rm S_{1}$を開いて,$\rm S_{2}$を閉じた.これを何度も繰り返していくと,$\rm C_{2}$の両端の電圧はある有限な値に近づいていった.その値を求めよ.
<解答>

今回は,漸化式を立てて解く方法を紹介します.
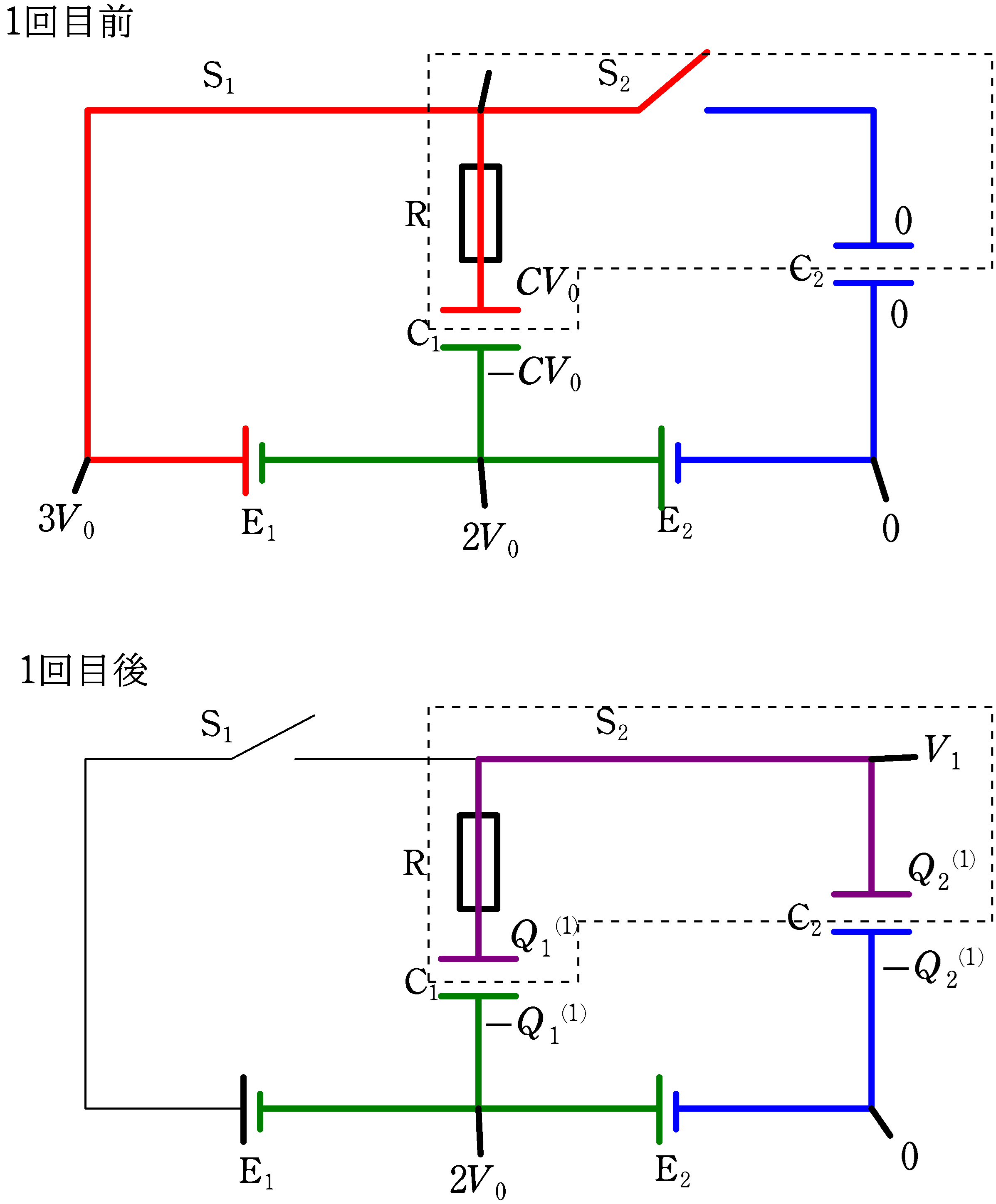
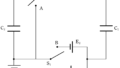
下図は,はじめて$\rm S_{1}$を入れて十分時間が経過し,$\rm C_{1}$の電荷が蓄えられ,$\rm S_{1}$を開いたのちに$\rm S_{2}$を閉じる直前(「1回目前」とよぶ.)と$\rm S_{2}$を閉じて十分時間が経過した後(「1回目後」とよぶ.)の図です.
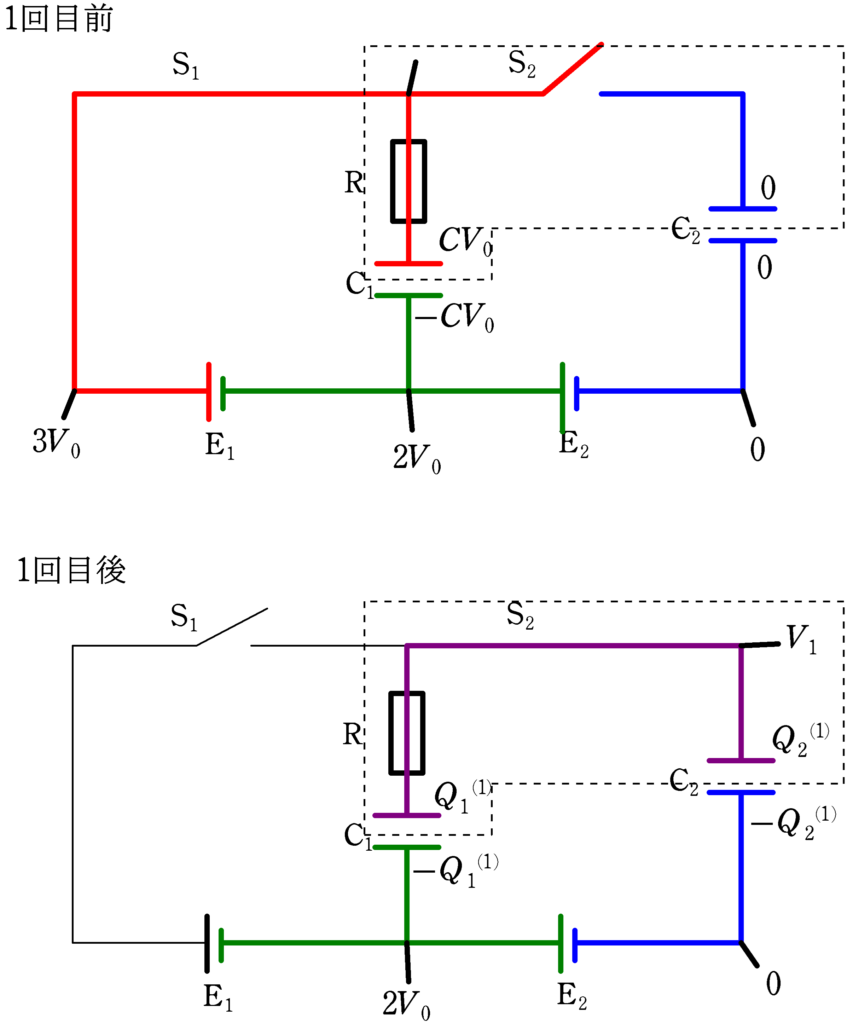

「1回目前」では,$\rm C_{1}$は起電力$V_{0}$の電池につないで充電したので,コンデンサーの式から,$CV_{0}$の電荷が蓄えられます.$\rm C_{2}$に蓄えられている電荷はまだ0です.
「1回目後」で$\rm C_{1}$,$\rm C_{2}$にそれぞれ$Q_{1}^{(1)}$,$Q_{2}^{(1)}$の電荷が蓄えられたとしましょう.
$\rm C_{2}$の下側の極板の電位を基準の0(青色部分)として,$\rm E_{2}$の起電力が$2V_{0}$であるから,$\rm C_{1}$の下側極板の電位は$2V_{0}$(緑色部分),$\rm C_{1}$,$\rm C_{2}$の上側の電位は未知なので,$V_{1}$とおきましょう.(紫色部分)
★ 点線で囲まれた部分の電荷保存則
$CV_{0}+0=Q_{1}^{(1)}+Q_{2}^{(2)}$ $\dots (\ast)$
★ 「1回目後」の$\rm C_{1}$,$\rm C_{2}$のコンデンサーの式
$Q_{1}=C(V_{1}-2V_{0})$ , $Q_{2}=C(V_{1}-0)$ $\dots (2\ast)$
★$(2\ast)$を$(\ast)$に代入して
$\eqalign{\cancel{C}V_{0}&=\cancel{C}(V_{1}-2V_{0})+\cancel{C}V_{1}\cr V_{1}&=\dfrac{3}{2}V_{0}}$ $\dots (\clubsuit)$

では,「$n$回目」の操作を考えましょう.
「$n$回目前」についても,$\rm C_{1}$は起電力$V_{0}$の電池$\rm E_{1}$につないだ後なので,$CV_{0}$の電荷が蓄えられています.
また,$\rm C_{2}$の方は「$n-1$回後」の操作を終えたままので電荷なので,$Q_{2}^{(n-1)}$の電荷が蓄えられています.
「$n-1$回目後」の$\rm C_{1}$,$\rm C_{2}$の上側極板の電位を$V_{n-1}$とすると
$Q_{2}^{(n-1)}=CV_{n-1}$ $\dots (3\ast)$
が成り立ちます.
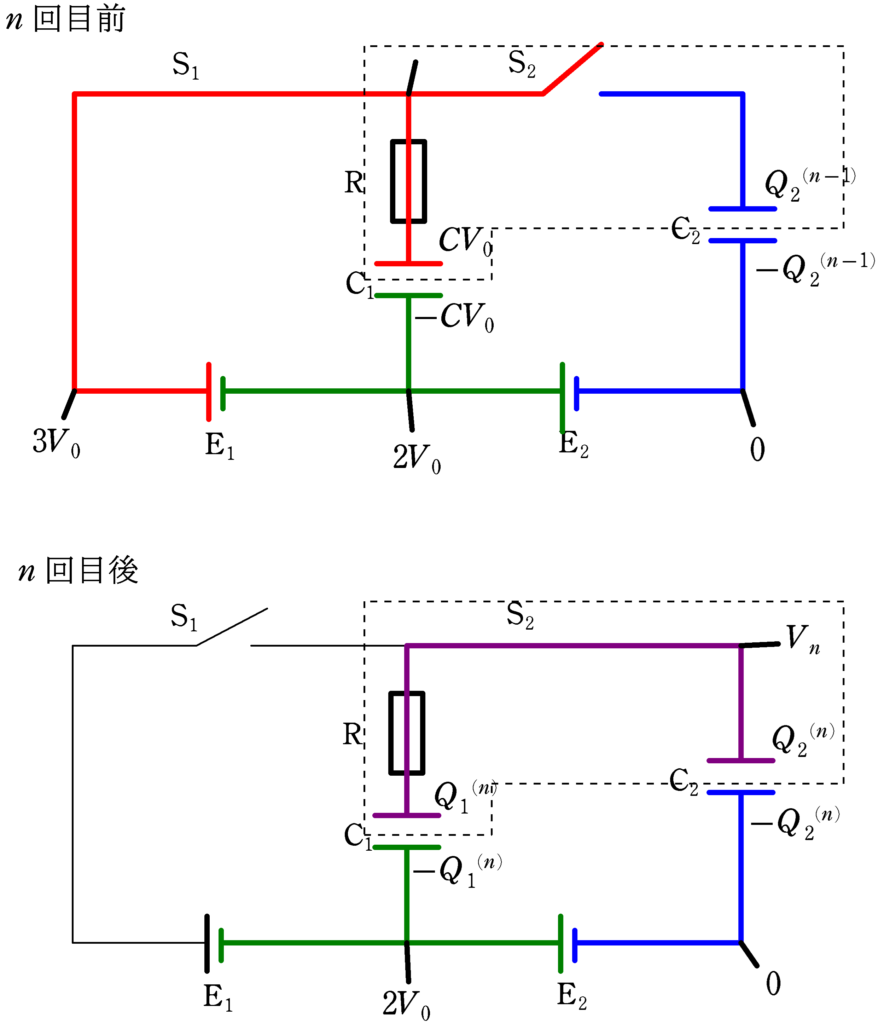

「$n$回目後」の$\rm C_{1}$,$\rm C_{2}$に蓄えられた電荷を$Q_{1}^{(n)}$,$Q_{2}^{(n)}$とし,$\rm C_{1}$,$\rm C_{2}$の上側極板の電位を$V_{n}$とします.
勿論,$\rm C_{1}$の下側極板の電位は$\rm E_{2}$の電池起電力が$2V_{0}$であることから,$2V_{0}$となります.
★ 点線部分の電荷保存則
$CV_{0}+Q_{2}^{(n-1)}=Q_{1}^{(n)}+Q_{2}^{(n)}$ $\dots (4\ast)$
★ $n$回目後の$\rm C_{1}$,$\rm C_{2}$のコンデンサーの式
$Q_{1}^{(n)}=C(V_{n}-2V_{0})$ ,$Q_{2}^{(n)}=C(V_{n}-0)$ $\dots (5\ast)$
★ $(3\ast)$,$(5\ast)$を$(4\ast)$に代入.
$\cancel{C}V_{0}+\cancel{C}V_{n-1}=\cancel{C}(V_{n}-2V_{0})+\cancel{C}V_{n}$
$\therefore V_{n}=\dfrac{1}{2}V_{n-1}+\dfrac{3}{2}V_{0}$

$V_{1}=\dfrac{3}{2}V_{0}$$(\clubsuit)$,$V_{n}=\dfrac{1}{2}V_{n-1}+\dfrac{3}{2}V_{0}$を解けばいいんだね.
$V_{n}-3V_{0}=\dfrac{1}{2}(V_{n-1}-3V_{0})$
と変形する.数列$\{V_{n}-3V_{0}\}$は,初項$V_{1}-3V_{0}=\dfrac{3}{2}V_{0}-3V_{0}=-\dfrac{3}{2}V_{0}$,公比$\dfrac{1}{2}$の等比数列だから
$V_{n}-3V_{0}=-\dfrac{3}{2}V_{0}\left(\dfrac{1}{2}\right)^{n-1}$
$\therefore V_{n}=3V_{0}-\dfrac{3}{2}V_{0}\left(\dfrac{1}{2}\right)^{n-1}$ $\dots (\sharp)$

$(\sharp)$の式において,$n\to\infty$とすると,$\left(\dfrac{1}{2}\right)^{n-1}\to 0$となるので,$V_{n}$は$3V_{0}$に近づいていくね.
したがって,$\rm C_{2}$の電圧は$3V_{0}$(答)の電圧に近づくことがわかったね.
これは,こちらでも内容と同じだね.

コメント