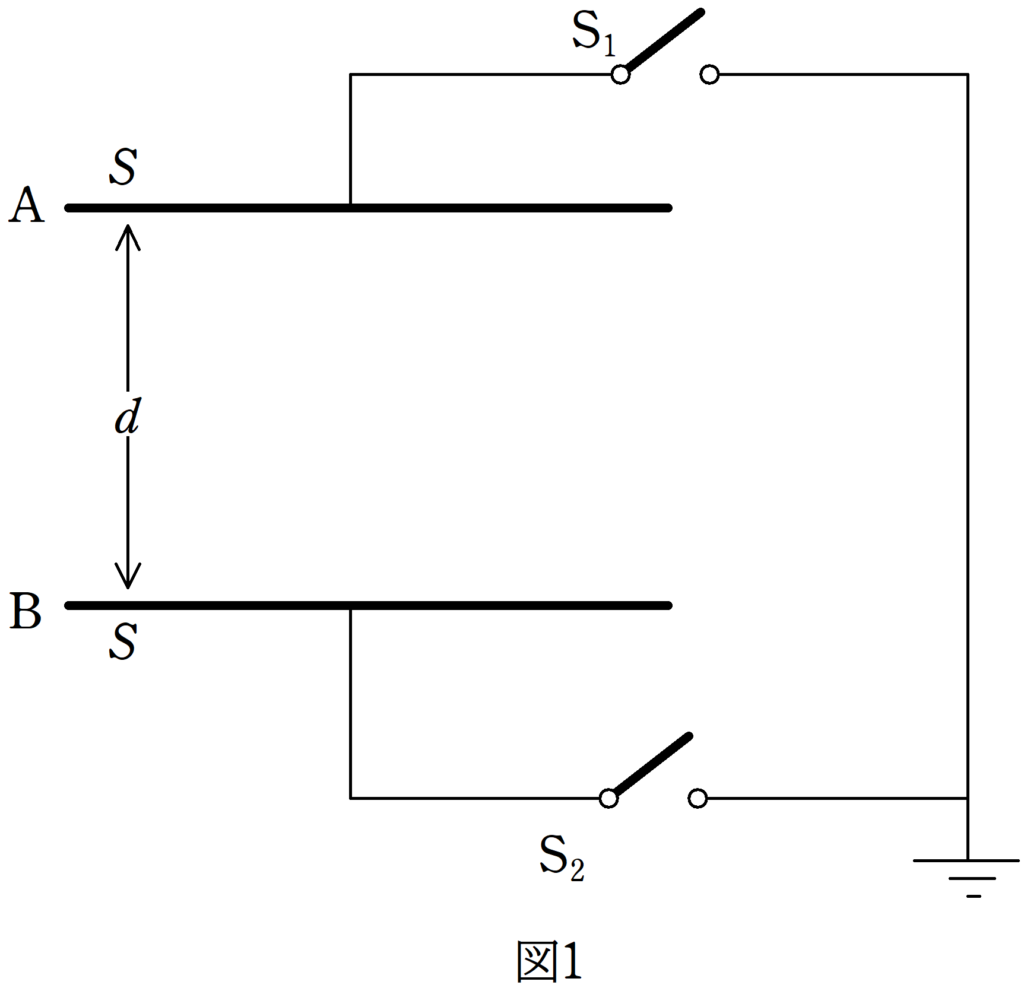
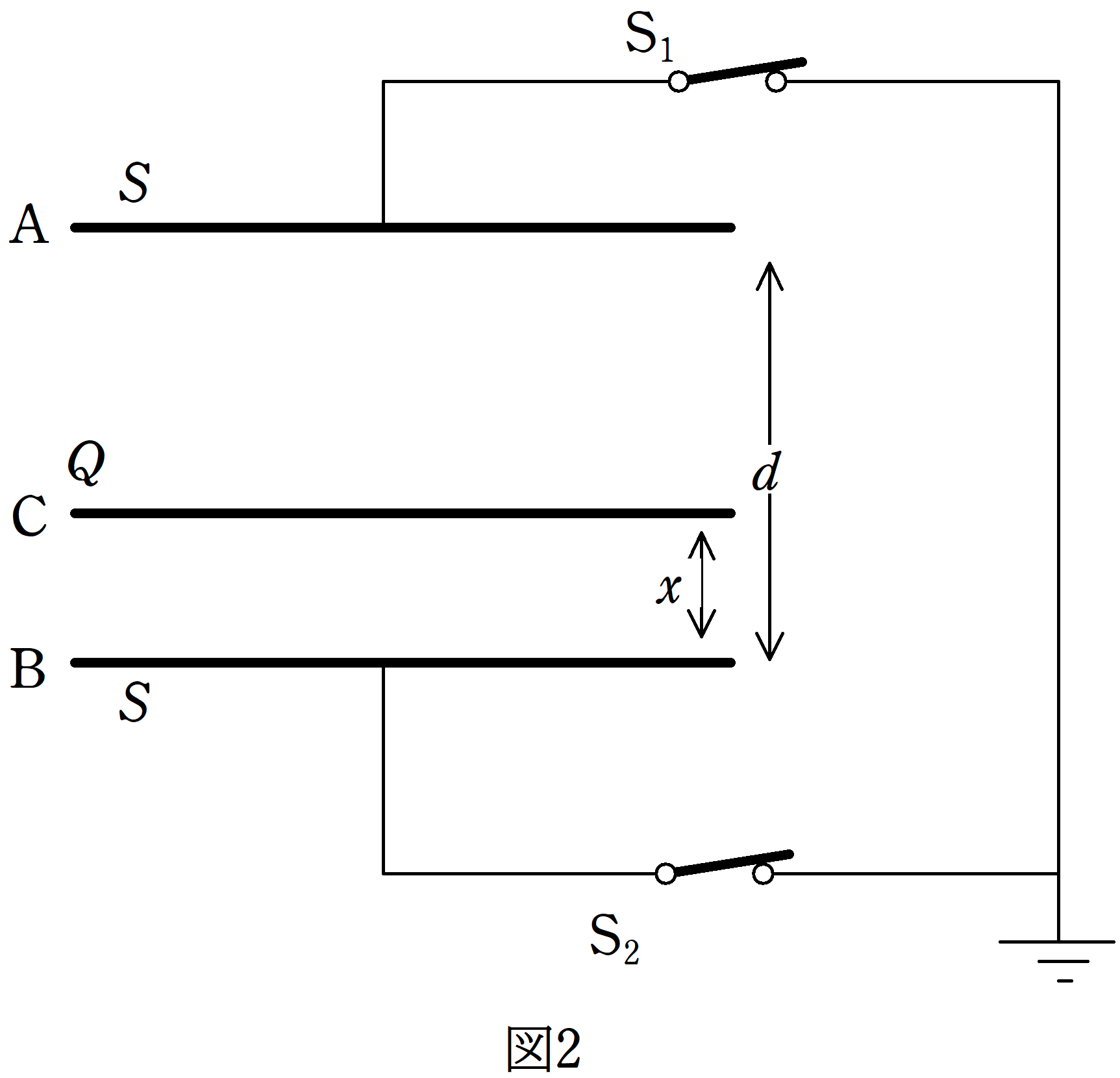
面積$S$の同形の極板A,Bが距離$d$を隔てて平行になるように固定されている.
図1のように,スイッチ$\rm S_{1}$,$\rm S_{2}$とアースを接続する.
はじめ,スイッチは開かれていて,極板A,Bには電荷が蓄えられていないとする.
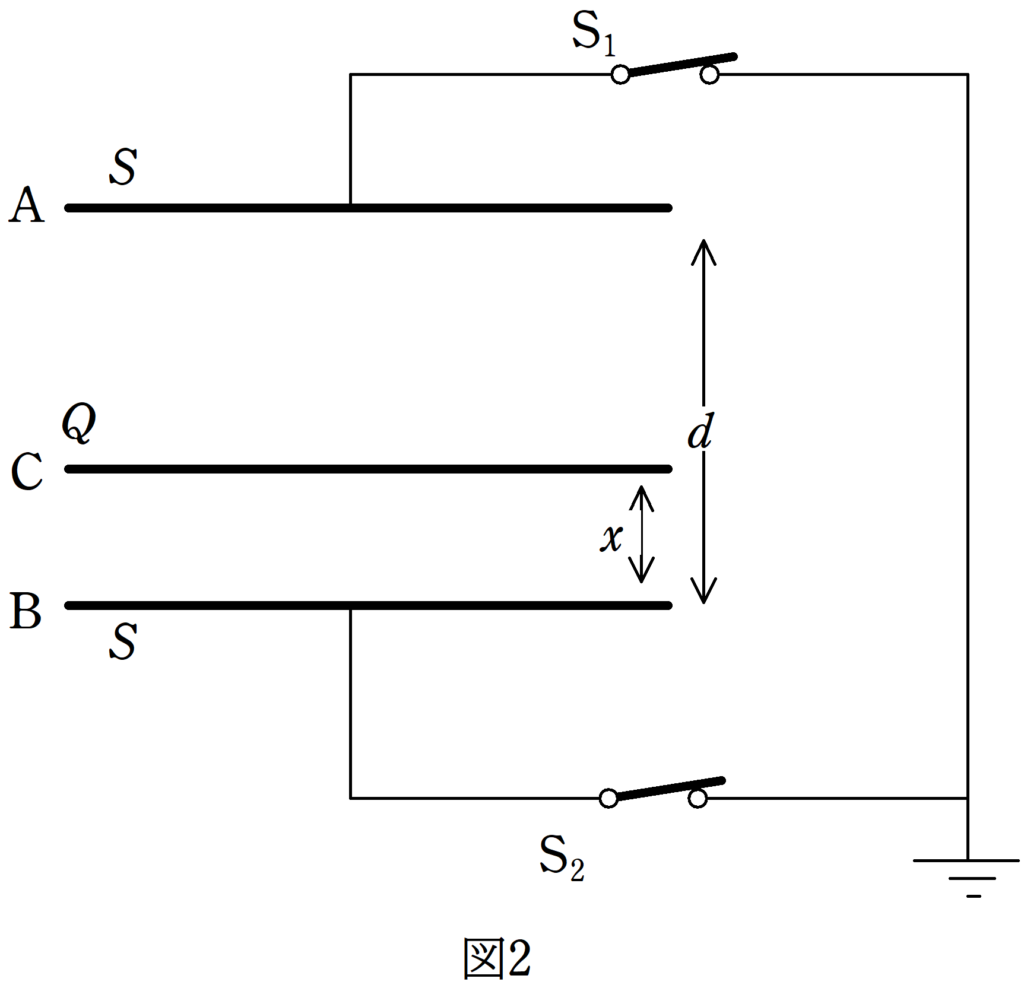
図1の状態から,スイッチ$\rm S_{1}$,$\rm S_{2}$を閉じ,極板A,Bと同形で面積$S$で電荷$Q$($Q>0$)が帯電している極板Cを極板A,Bと平行になるように挿入する.極板Cを挿入した位置は極板Bから距離$x$($0<x<d$)であった.
このとき,極板Aと極板Bに蓄えている電荷$Q_{\rm A}$,$Q_{\rm B}$を求めよ.
ただし,空気中の誘電率を$\varepsilon_{0}$とする.
<解答>

前回の内容はこちらです.
電荷保存則とコンデンサーの式を復習しておきましょう.
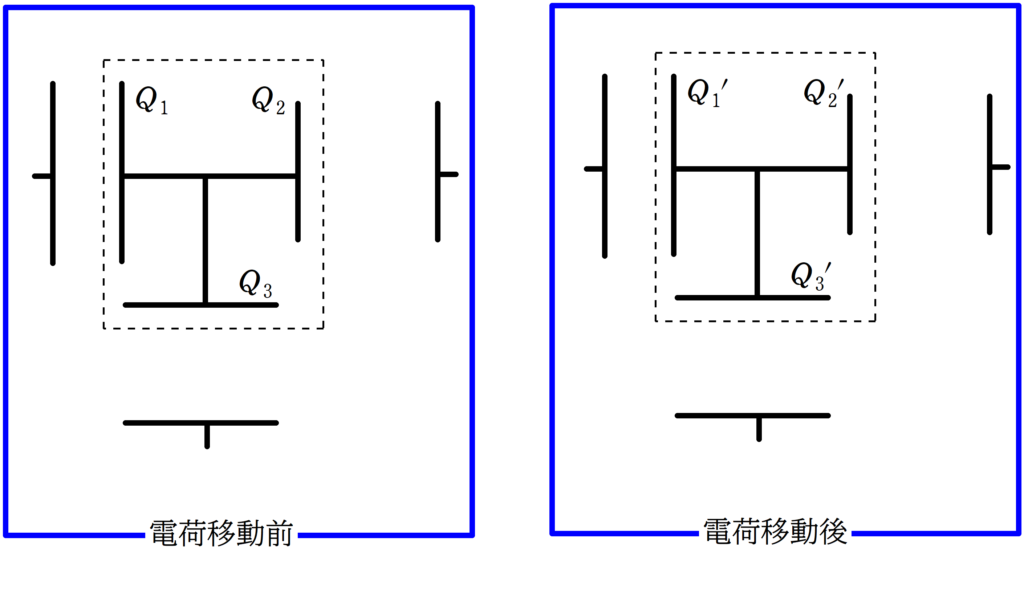
孤立した部分の電荷の総和は変化しない.これを電荷保存則という.
たとえば,上図のように点線部分の孤立した場所の電荷について考えると
$Q_{1}+Q_{2}+Q_{3}=Q_{1}^{\prime}+Q_{2}^{\prime}+Q_{3}^{\prime}$
が成り立つ.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.

極板を挿入する問題では,次のように,2つのコンデンサーに分けて考えるとよいでしょう.
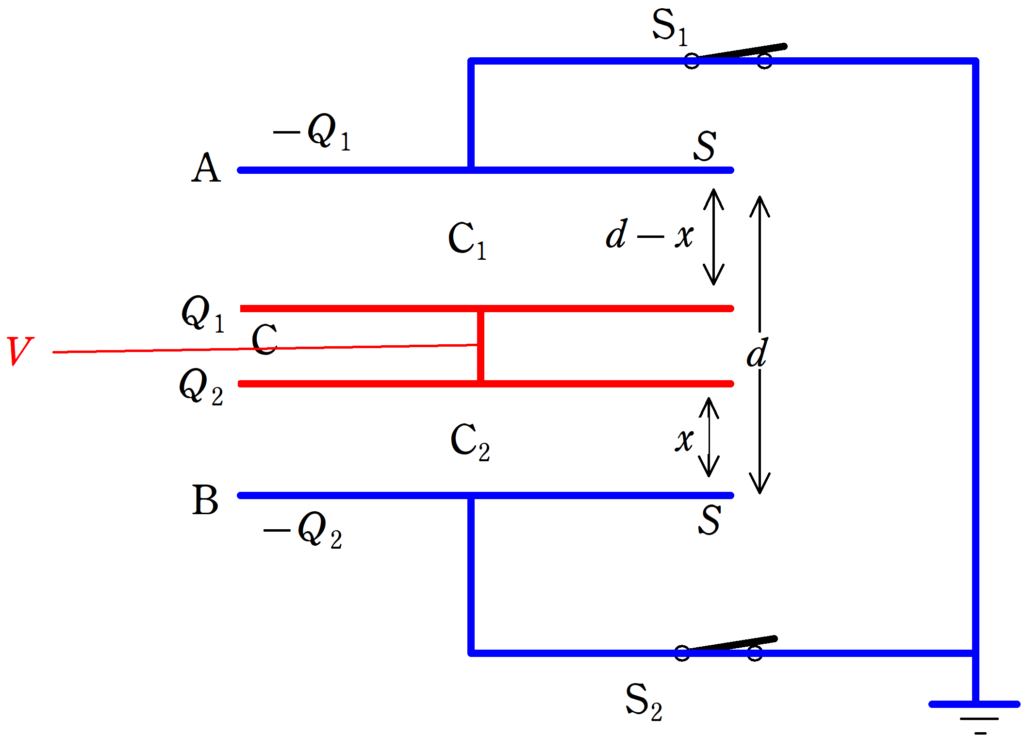

極板Cと極板Aで形成されるコンデンサーを$\rm C_{1}$,極板Cと極板Bで形成されるコンデンサーを$\rm C_{2}$とします.
$\rm C_{1}$の電気容量は,$\varepsilon_{0}\dfrac{S}{d-x}$,$\rm C_{2}$の電気容量は,$\varepsilon_{0}\dfrac{S}{x}$ですね.
青い部分の電位がアースにつながっているので0として,赤い部分の電位を$V$としましょう.
さらに,上図のように,電荷を設定します.
電荷保存則とコンデンサーの式を立てましょう.
★ 電荷保存則
赤い部分の電荷保存則
$Q_{1}+Q_{2}=Q$ $\dots (\ast)$
コンデンサー$\rm C_{1}$と$\rm C_{2}$の式
$Q_{1}=\varepsilon_{0}\dfrac{S}{d-x}V$ $\dots (2\ast)$
$Q_{2}=\varepsilon_{0}\dfrac{S}{x}V$ $\dots (3\ast)$
$(2\ast)$と$(3\ast)$を$(\ast)$に代入して$V$を求める
$\eqalign{\varepsilon_{0}\dfrac{S}{d-x}V+\varepsilon_{0}\dfrac{S}{x}V&=Q\cr \varepsilon_{0}S(\dfrac{1}{d-x}+\dfrac{1}{x})V&=Q\cr \varepsilon_{0}S(\dfrac{1}{d-x}+\dfrac{1}{x})V&=Q\cr V&=\dfrac{(d-x)x}{\varepsilon_{0}Sd}Q}$
これを$(\ast)$と$(2\ast)$に代入して
$\eqalign{Q_{1}&=\varepsilon_{0}\dfrac{S}{d-x}\cdot \dfrac{(d-x)x}{\varepsilon_{0}Sd}Q\\&=\dfrac{x}{d}Q }$
$\eqalign{Q_{2}&=\varepsilon_{0}\dfrac{S}{x}\cdot \dfrac{(d-x)x}{\varepsilon_{0}Sd}Q\\&=\dfrac{d-x}{d}Q}$
したがって,極板A,Bに蓄えられている電荷は
$Q_{\rm A}=-Q_{1}=-\dfrac{x}{d}Q$
$Q_{\rm B}=-Q_{2}=-\dfrac{d-x}{d}Q$

ちなみに,それぞれの極板の電荷分布は次のようになっています.
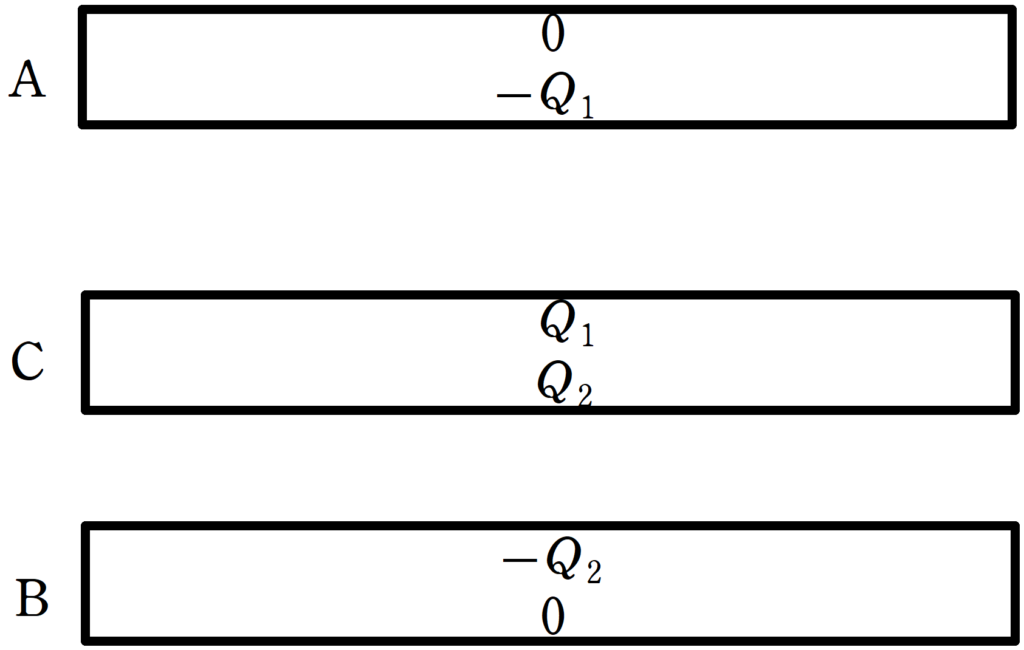

上のような電荷分布になる理由は,この記事でも説明しています.



コメント