
今回は2020年の東京大学の一部です.
今まで通り,次の式を立てる癖がついている人には易しい問題だったと思います.
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
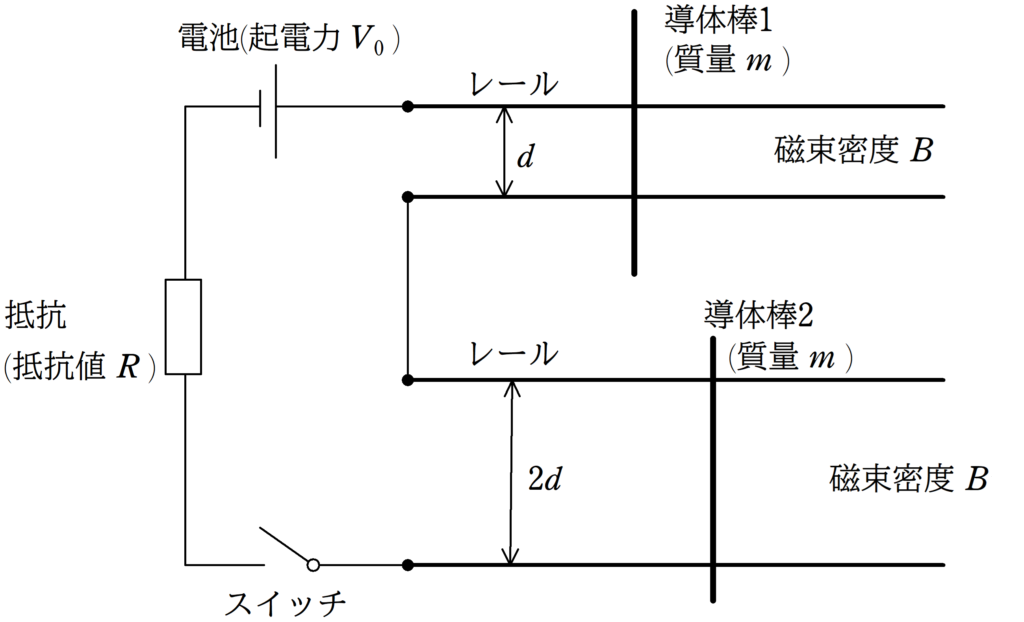
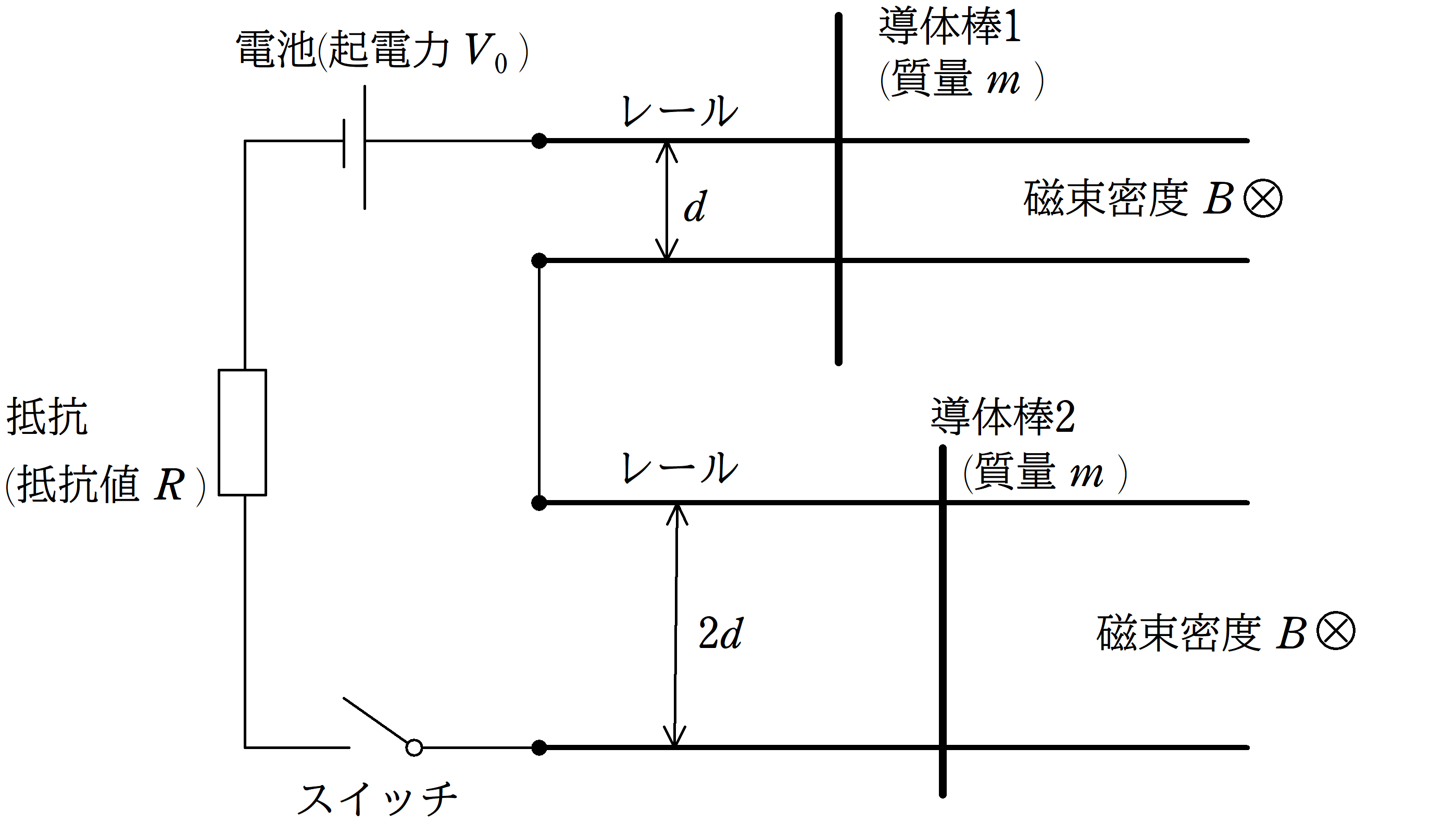
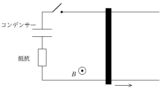
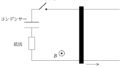
上図のように,水平面に置かれた,間隔$d$の平行なレールと間隔$2d$の平行なレールを導線でつなぎ,起電力$V_{0}$の電池,抵抗値$R$の抵抗,スイッチを取りつけた.
磁束密度の大きさ$B$の一様な磁場が全空間で鉛直下方向(紙面垂直奥向き)にかけられている.
スイッチが切られた状態で,図のように質量$m$の2つの導体棒1,2をそれぞれ間隔$d$,間隔$2d$のレール上に垂直に置き静止させたのち,スイッチを閉じたところ,導体棒1,2はともに右向きに動き始めた.
十分に時間が経ったのち,導体棒の速さは一定と見なせるようになった.
このとき,導体棒1,2の速さを$B , d , m , R , V_{0}$のうち,必要なものを用いてそれぞれ求めよ.
また,導体棒はレール方向のみに動けるものとし,摩擦や空気抵抗,導体棒の両端に発生する誘導電荷,および回路を流れる電流が作る磁場の影響は無視できるものとする.
<解答>

まずは,設定からしていきましょう.
スイッチを閉じた時刻を$t=0$とし,時刻$t$における導体棒1と導体棒2のそれぞれの速度を$v_{1}$,$v_{2}$,加速度を$a_{1}$,$a_{2}$,回路に流れる電流の大きさを$i$としましょう.
導体棒1,2の速度と加速度を異なるものとして設定しておく必要があるよ.
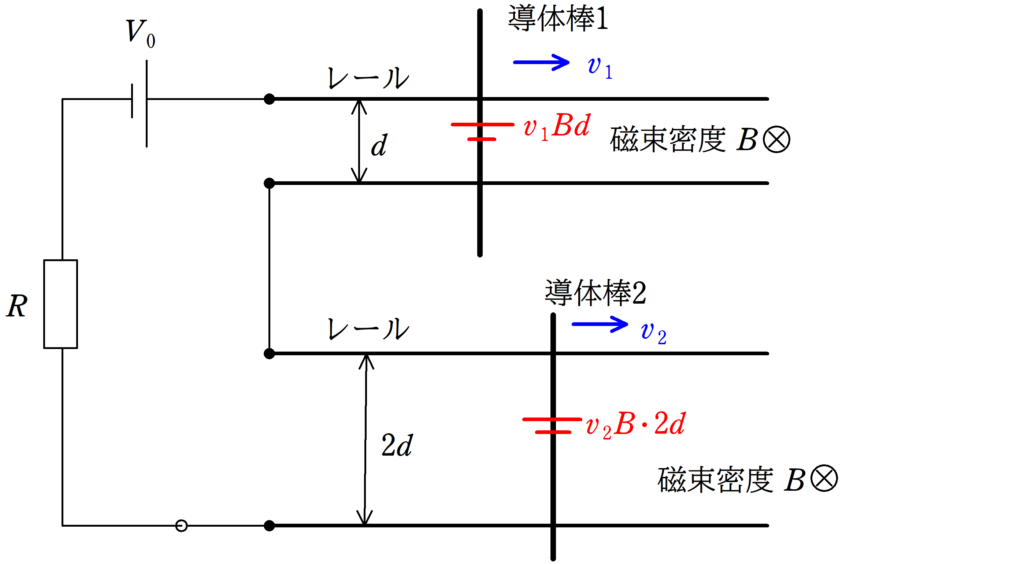

すると,導体棒1に生じる誘導起電力の大きさは,それぞれ$v_{1}Bd$,$v_{2}B\cdot 2d$となるね.
誘導起電力の向きは,レンツの法則を考えて上図の向きだね.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

さて,まずは「1.回路の式」だね.
★ キルヒホッフの法則
$V_{0}-v_{1}Bd-2v_{2}Bd-iR=0$
$\therefore i=\dfrac{V_{0}-v_{1}Bd-2v_{2}Bd}{R}$ $\dots (\ast)$
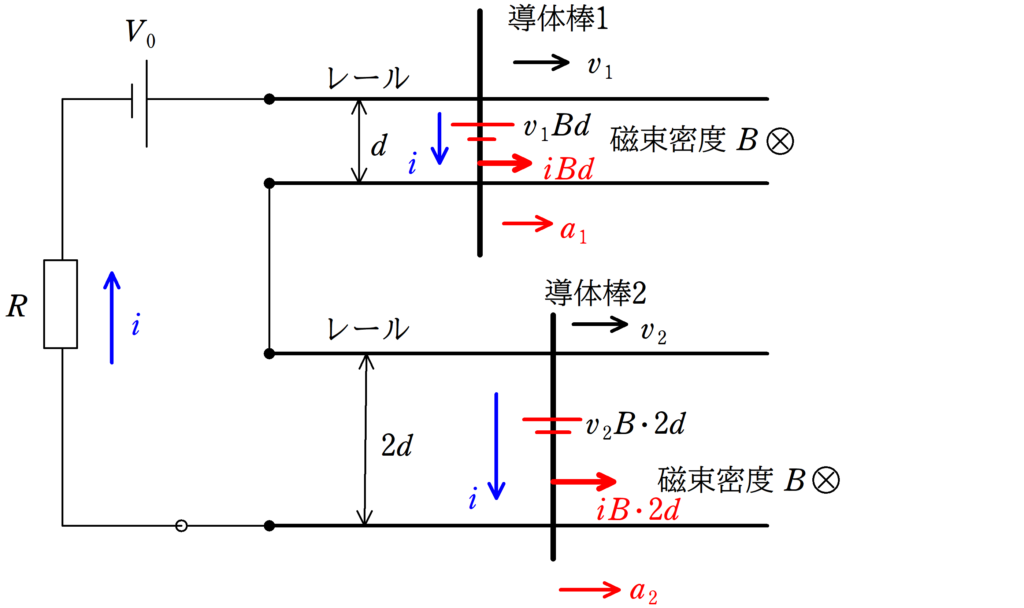

次に,「2.導体棒の運動に関する式」です.
磁場中を電流が流れているので,電磁力を受けます.
導体棒1,2それぞれの運動方程式を立てましょう.
★ 導体棒1の運動方程式
$ma_{1}=iBd$ $\dots (2\ast)$
★ 導体棒2の運動方程式
$ma_{2}=iB\cdot 2d$ $\dots (3\ast)$
$(2\ast)$,$(3\ast)$より,
$2a_{1}=a_{2}$
の関係を導くことができます.
すると,加速度の定義から,$a_{1}=\dfrac{\Delta v_{1}}{\Delta t}$,$a_{2}=\dfrac{\Delta v_{2}}{\Delta t}$なので
$2\dfrac{\Delta v_{1}}{\Delta t}=\dfrac{\Delta v_{2}}{\Delta t}$
ここで,$t=0$のとき,$v_{1}=v_{2}=0$なので,上の式と合わせて
$2v_{1}=v_{2}$ $\dots (4\ast)$
を得ます.
すると,$(\ast)$の$i=\dfrac{V_{0}-v_{1}Bd-2v_{2}Bd}{R}$は
$i=\dfrac{V_{0}-5v_{1}Bd}{R}$ $\dots (5\ast)$
$(2\ast)$で$a_{1}=\dfrac{\Delta v_{1}}{\Delta t}$を代入して
$m\dfrac{\Delta v_{1}}{\Delta t}=iBd$
この式に$(5\ast)$を代入して
$m\dfrac{\Delta v_{1}}{\Delta t}=\dfrac{V_{0}-5v_{1}Bd}{R}\cdot Bd$
$\dfrac{\Delta v_{1}}{\Delta t}=-\dfrac{5B^{2}d^{2}}{mR}v_{1}+\dfrac{V_{0}Bd}{mR}$ $(\clubsuit)$

$(\clubsuit)$は終端速度型の運動方程式と同じ形だね.
質量を$m$,加速度を$a$,速度を$v$,$C$を定数とすると
$ma=-kv+C$
は終端速度型の運動方程式である.
終端速度型の運動方程式は次の特徴がある.
十分時間が経つと,速度が一定(加速度が0)になる.
速度が一定になったときの速度を終端速度という.
終端速度は運動方程式に$a=0$を代入して
$0=-kv+C$ $\therefore v=\dfrac{C}{k}$
また,$t=0$のときの速度を$v_{0}$とすると,そのときの加速度($v-t$グラフの傾き)は
$a=\dfrac{-kv_{0}+C}{m}$
となる.

つまり,十分時間が経つと,$\dfrac{\Delta v_{1}}{\Delta t}=0$となるんだね!
なぜ,このようになるのかは,次の記事でも説明しているよ.
$(\clubsuit)$に$\dfrac{\Delta v_{1}}{\Delta t}=0$を代入して,$v_{1}$を求めます.
$\eqalign{0&=-\dfrac{5B^{2}d^{2}}{mR}v_{1}+\dfrac{V_{0}Bd}{mR}\cr v_{1}&=\dfrac{V_{0}}{5Bd}}$
$(4\ast)$より,
$v_{2}=2v_{1}=\dfrac{2V_{0}}{5Bd}$

ということで,導体棒1と2の速度はそれぞれ
$\dfrac{V_{0}}{5Bd}$,$\dfrac{2V_{0}}{5Bd}$
となります.
次回の内容はこちらです.



コメント
[…] […]