[標準]導体棒とコンデンサー① | Physicmath（フィジクマス）

PHYさん

今までは，回路素子として抵抗のみを扱ってきましたが，今回はコンデンサーを使った問題を解いていきます．

NEKO

今までと違ったことをする必要があるの？？

PHYさん

いえ，変わりません．

ただ，コンデンサーの問題なので，次の2つの式はチェックしておきましょう．

コンデンサーの基本式

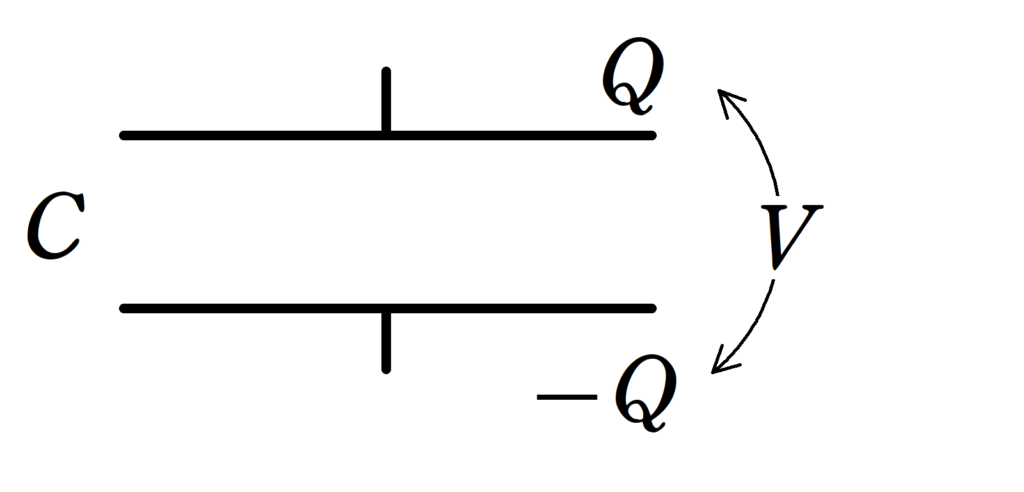
コンデンサーの電気容量（静電容量）を$C$，コンデンサーにかかる電圧を$V$，蓄えられた電気量を$Q$とすると，

$Q=CV$

の関係がある．

電流の定義

時間$\Delta t$の間に電気量$\Delta Q$が通過するときの電流の大きさ$i$は

$i=\dfrac{\Delta Q}{\Delta t}$

PHYさん

では問題を解いてみましょう．

その他の導体棒の問題はこちらにまとめてあります．

問題

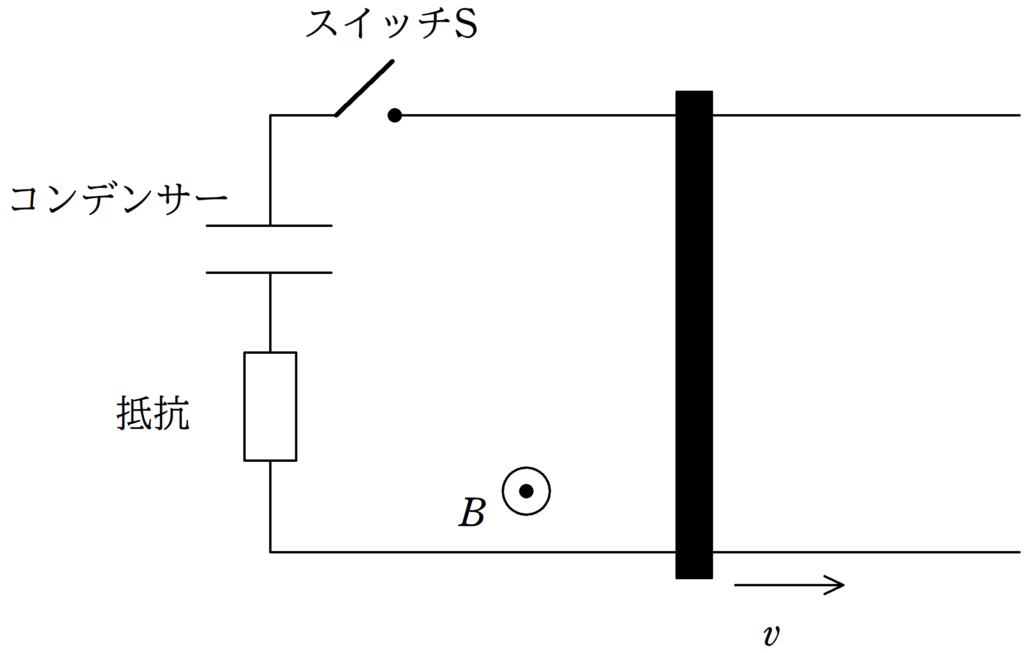
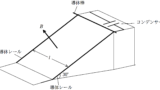
上図のように，水平面に導体レールを平行に敷き，その間隔を$l$にして固定する．

また，電気抵抗$R$の抵抗，電気容量$C$のコンデンサー，スイッチを上図のようにつないだ．

この空間全範囲に鉛直上向き（画面奥から手前方向）大きさ$B$の一様な磁束密度をかけた．

2本の導体レールの上と垂直になるように，質量$m$の導体棒をおき，図の向きに速さ$v$を与えた．

速さ$v$を維持したままスイッチを閉じ，その後も外力を加え速さ$v$を維持した．

このとき，十分時間が経ったときのコンデンサーに蓄えられる電荷を求めよ．

ただし，スイッチを閉じる前にコンデンサーには電荷が蓄えられていなかったものとする．

<解答>

NEKO

次の2つのことをチェックしておきましょう．

導体棒の問題で立てて欲しい3つの式

回路の式（オームの法則，コンデンサーの基本式，電荷保存則など）
導体棒の運動に関する式（つり合いの式，運動方程式，運動量保存則など）
導体棒と回路の系全体のエネルギー収支の式

導体棒に生じる誘導起電力の公式（直線運動）

PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，

$V=v_{\perp}Bl$

NEKO

設定をしましょう．

スイッチを閉じた時刻を$t=0$とし，時刻$t$に回路に流れている電流を$i$，コンデンサーに蓄えらえている電荷を$q$とします．

NEKO

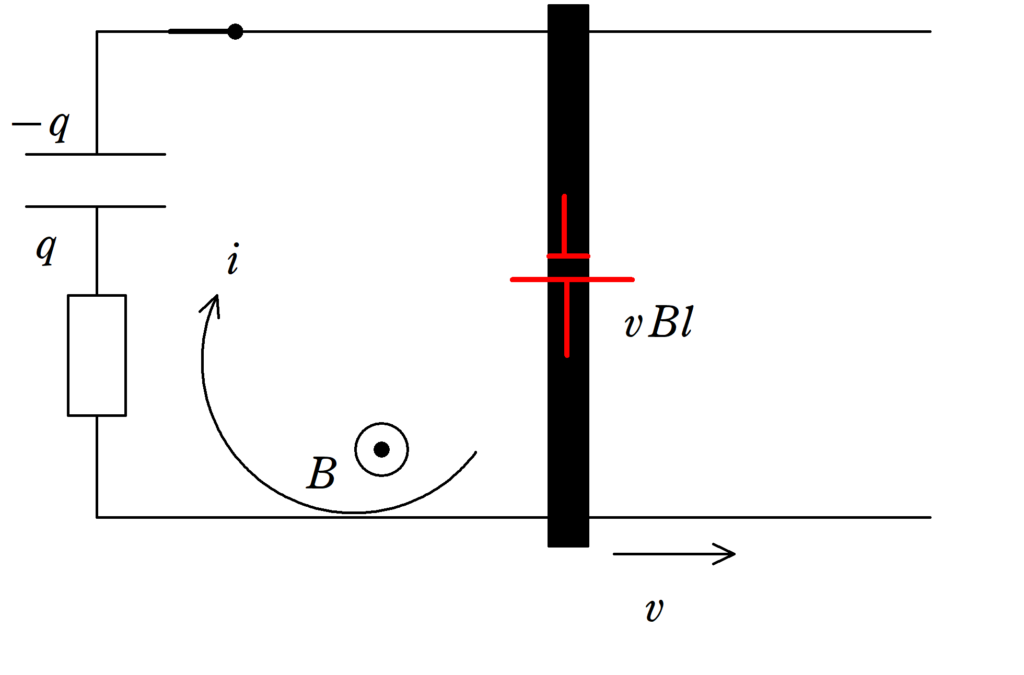
導体棒は常に速さ$v$に保たれているので，導体棒に生じる誘導起電力は$vBl$ですね．

また，コンデンサーにかかる電圧を$V_{\rm C}$とすると，コンデンサーの基本式より

$q=CV_{\rm C}$

$\therefore　V_{\rm C}=\dfrac{q}{C}$

となります．

その上で，「1.回路の式」を立てていきましょう．

★　キルヒホッフの法則

$vBl-Ri-V_{\rm C}=0$

$V_{\rm C}=\dfrac{q}{C}$より

$vBl-Ri-\dfrac{q}{C}$　$\dots　(\ast)$

★　電流の定義式

$i=\dfrac{\Delta q}{\Delta t}$　$\dots　(2\ast)$

$(2\ast)$を$(\ast)$に代入して

$vBl-R\dfrac{\Delta q}{\Delta t}-\dfrac{q}{C}=0$

$\therefore　\dfrac{\Delta q}{\Delta t}=-\dfrac{1}{RC}q+\dfrac{vBl}{R}$　$\dots　(\clubsuit)$

NEKO

$(\clubsuit)$の式はいつもの終端速度型の運動方程式と同じ形だね！

($a=\dfrac{\Delta v}{\Delta t}$だから，対応関係を考えれば同じ)

こちらの記事のも書いてあるよ．

終端速度型の運動方程式

質量を$m$，加速度を$a$，速度を$v$，$C$を定数とすると

$ma=-kv+C$

は終端速度型の運動方程式である．

終端速度型の運動方程式は次の特徴がある．

十分時間が経つと，速度が一定（加速度が0）になる．

速度が一定になったときの速度を終端速度という．

終端速度は運動方程式に$a=0$を代入して

$0=-kv+C$　$\therefore　v=\dfrac{C}{k}$

また，$t=0$のときの速度を$v_{0}$とすると，そのときの加速度（$v-t$グラフの傾き）は

$a=\dfrac{-kv_{0}+C}{m}$

となる．

NEKO

つまり，十分時間が経つと

$\dfrac{\Delta q}{\Delta t}=0$

となるんだね．

十分時間が経つと，$\dfrac{\Delta q}{\Delta t}=0$となるので，$(\clubsuit)$より

$\eqalign{0&=-\dfrac{1}{RC}q+\dfrac{vBl}{R}\cr q&=vBlC}$

答え：十分時間が経ったときに蓄えられる電荷は$vBlC$

PHYさん

この問題はわざわざ式を立てなくても電流が0になるときを考えればよいのですが，より難しい問題を確実に解くには式を立てる癖をつけておくとよいでしょう．

次回の内容はこちらです．