
今回は,ディーゼルエンジンにも関係する,ディーゼルサイクルを扱います.
さっそく問題をみてみましょう.
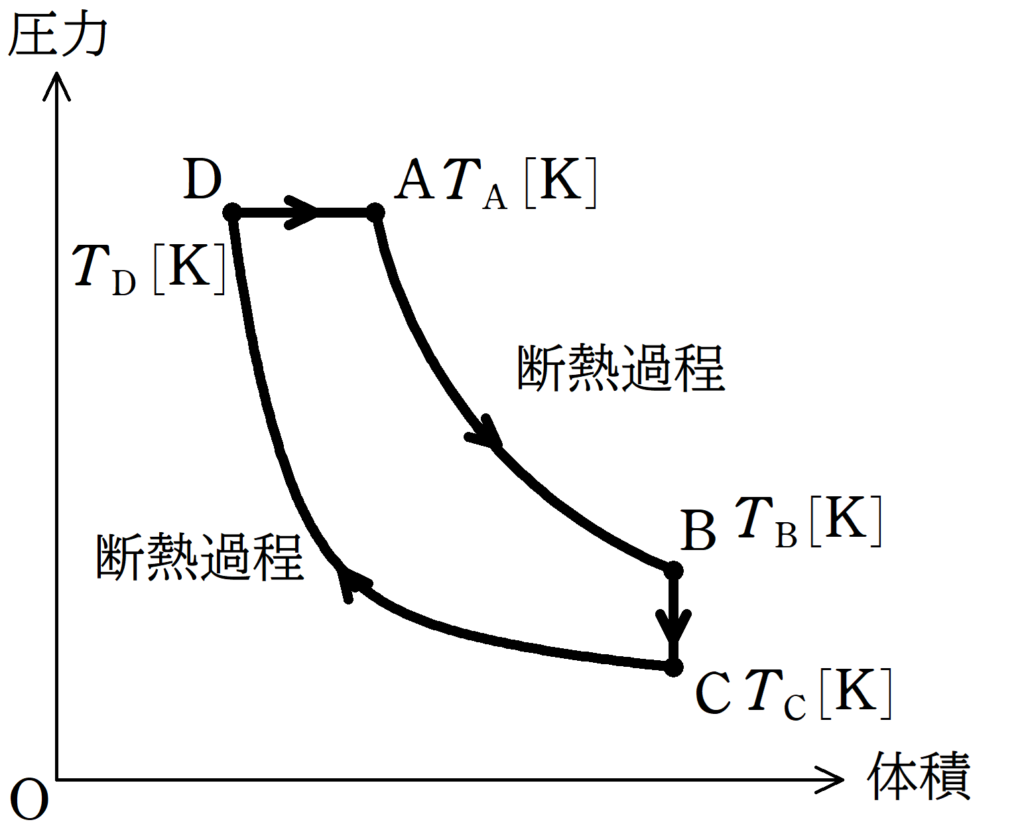
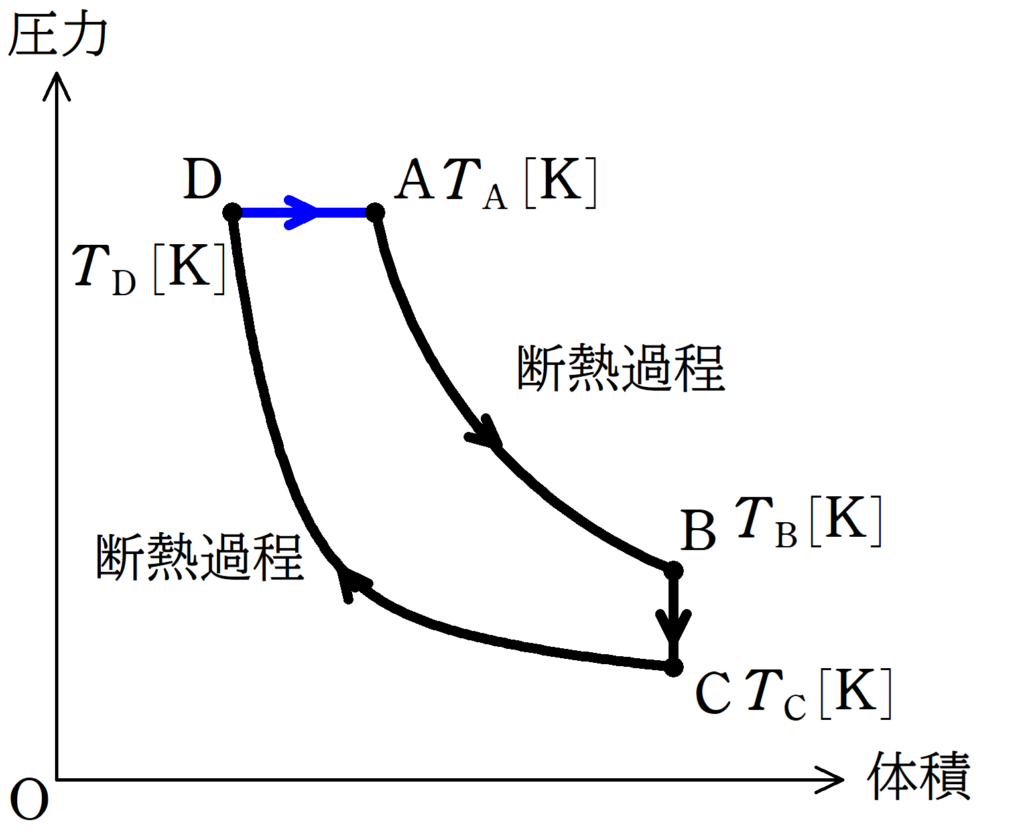
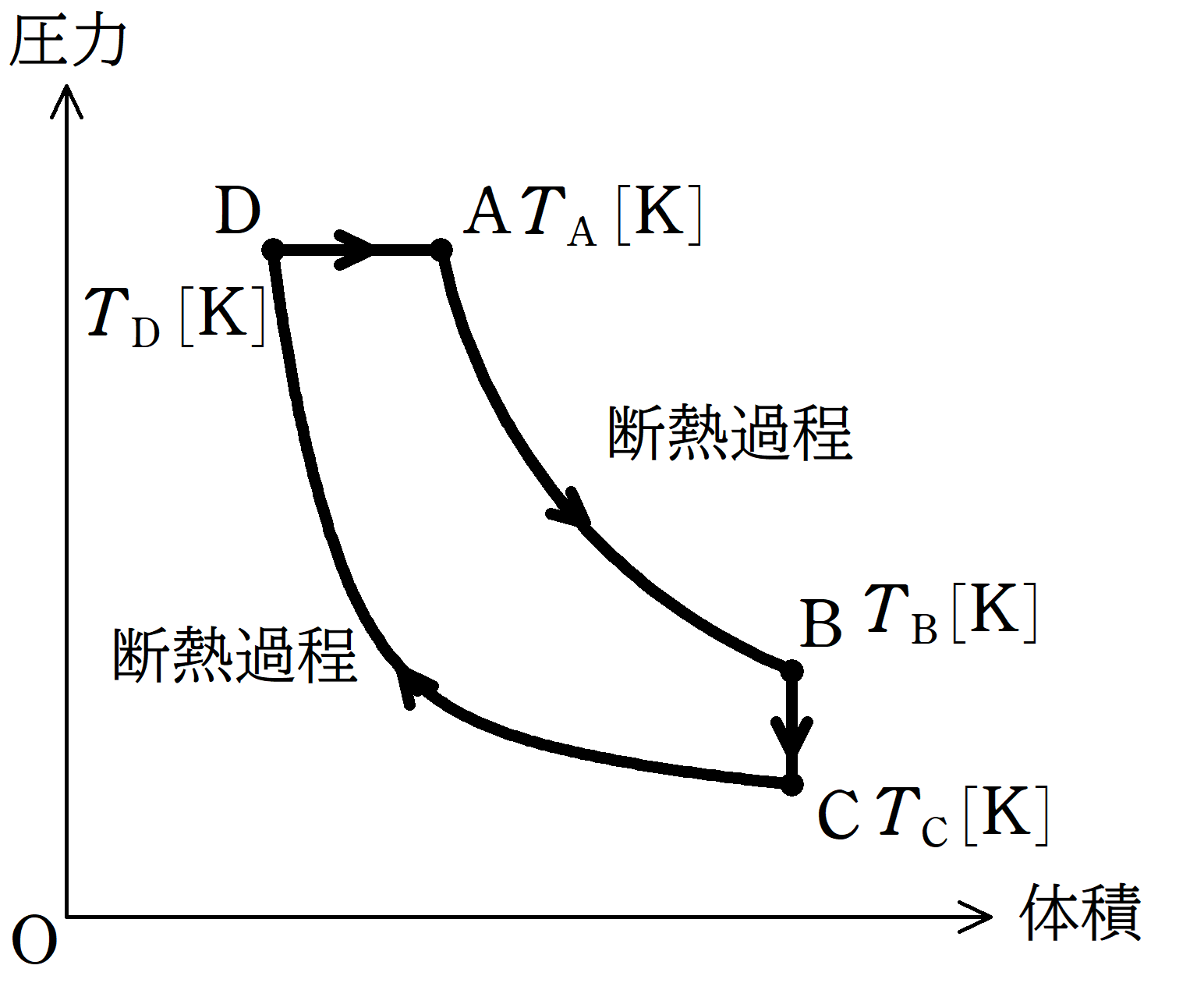
状態Aから状態Bまでは断熱変化で気体を膨張させ,状態Bから状態Cまでは,体積を一定に保ったまま,圧力を下げる.
また,状態CからDまでは,断熱変化で気体を圧縮し,状態Dから状態Aまでは,圧力を一定に保ったまま膨張させる.
状態A,B,C,Dの絶対温度を$T_{\rm A}[\rm K]$,$T_{\rm B}[\rm K]$,$T_{\rm C}[\rm K]$,$T_{\rm D}[\rm K]$とし,気体は物質量$1\rm mol$の単原子分子理想気体である.
気体定数を$R[\rm J/mol\cdot K]$として次の問いに答えよ.
(1) $T_{\rm A}$と$T_{\rm B}$の大小関係を答えよ.また,$T_{\rm B}$と$T_{\rm C}$,$T_{\rm C}$と$T_{\rm D}$,$T_{\rm D}$と$T_{\rm A}$についてもそれぞれ答えよ.
(2) 過程AからBの間に気体がした仕事$W_{\rm AB}[\rm J]$を求めよ.
(3) 過程BからCまでの間の気体の熱量$Q_{\rm BC}[\rm J]$を求めよ.
(4) 過程CからDまでの気体がした仕事$W_{\rm CD}[\rm J]$を求めよ.
(5) 過程DからAまでに気体がした仕事$W_{\rm DA}[\rm J]$と,熱量$Q_{\rm DA}[\rm J]$を求めよ.
<解答>
(1)
● $T_{\rm A}$と$T_{\rm B}$

$T_{\rm A}$と$T_{\rm B}$の大小関係は熱力学第一法則を利用してみましょう.
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
★ 過程AからBの熱力学第一法則
断熱変化であるから,熱量$Q_{\rm AB}=0$.したがって
$\Delta U_{\rm AB}=Q_{\rm AB}-W_{\rm AB}=0-W_{\rm AB}$

ここで,AからBは体積が膨張しているから,気体は正の仕事をしているね.
だから,上の式より$\Delta U_{\rm AB}<0$となります.
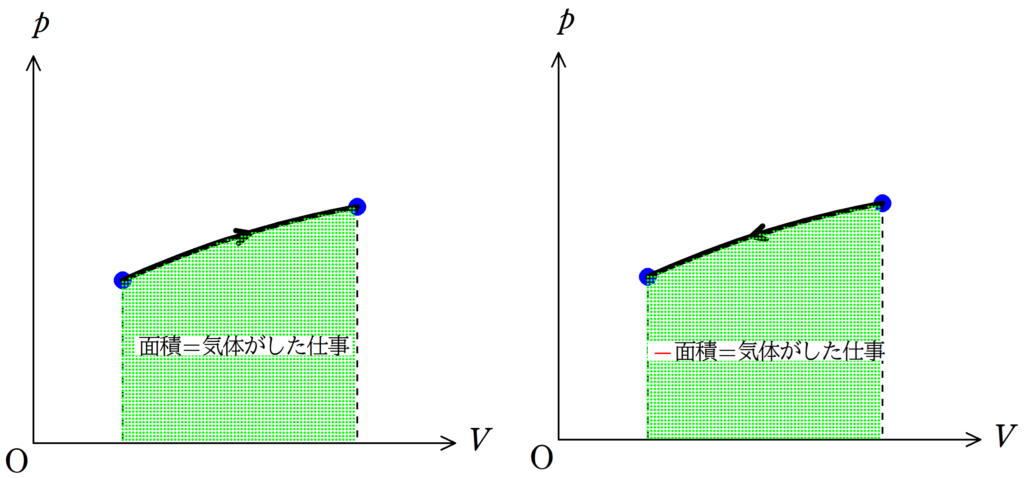
気体がした仕事は上図のように緑色部分の面積を求めることで計算ができる.
ただし,状態変化の矢印が右向きのときは
面積=気体がした仕事
であるが,状態変化の矢印が左向きのときは
-面積=気体がした仕事
である.

内部エネルギーの変化の正負と温度変化の正負は一致するだったよね.(下を参照)
内部エネルギーの変化が負であることから,温度が下がることがわかります.
したがって,$T_{\rm A}>T_{\rm B}$
問題文に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
● $T_{\rm B}$と$T_{\rm C}$

$T_{\rm B}$と$T_{\rm C}$については,$pV$グラフの面積を利用しましょう.
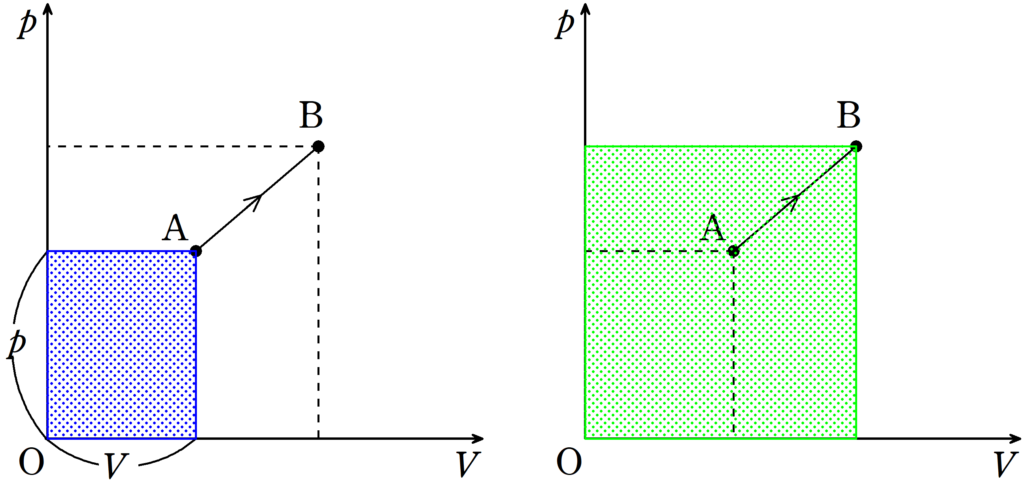
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する.
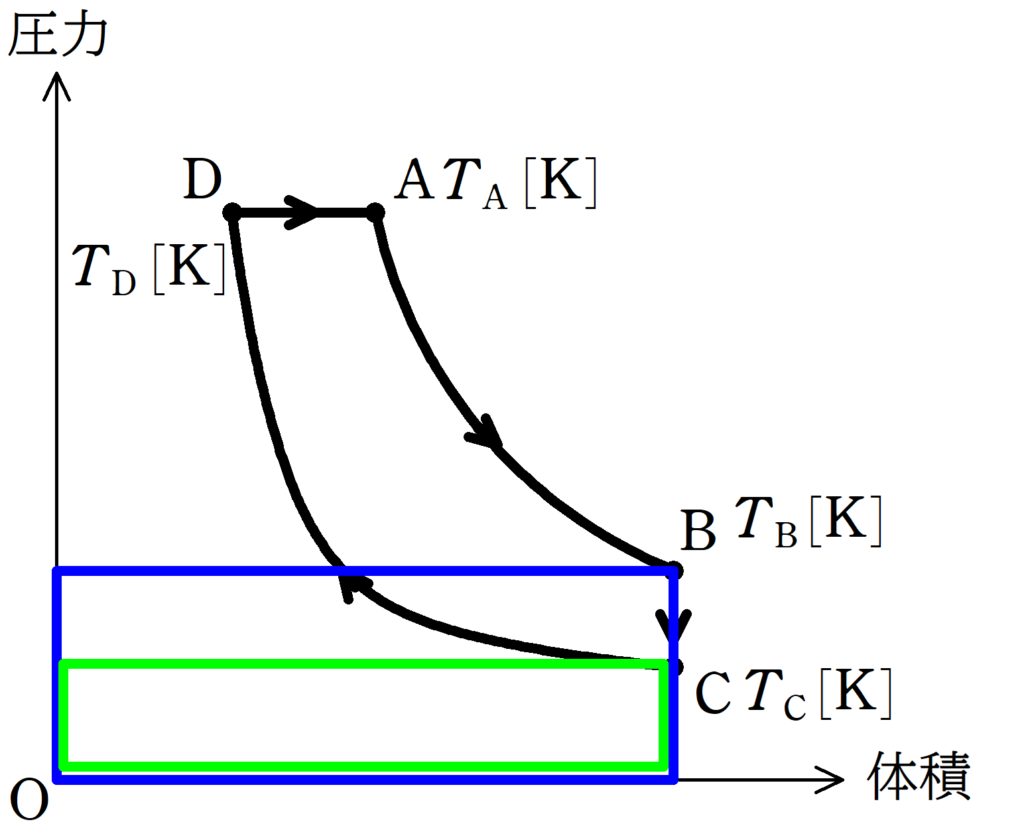

緑の長方形の面積より,青の長方形の面積の方が大きいね.
したがって$T_{\rm B}>T_{\rm C}$
● $T_{\rm C}$と$T_{\rm D}$

こちらも熱力学第一法則を利用しましょう.
★ 過程CからDの熱力学第一法則
断熱変化なので,$Q_{\rm CD}=0$.
$\Delta U_{\rm CD}=0-W_{\rm CD}>0$

CからDまでは体積が減少しているから,気体がした仕事は負だね.
だから,$-W_{\rm CD}>0$となって,内部エネルギーの変化も正になるよ.
つまり,温度が上昇するんだね.
したがって,$T_{\rm C}<T_{\rm D}$
● $T_{\rm D}$と$T_{\rm A}$

過程DからAも面積で判断しましょう.
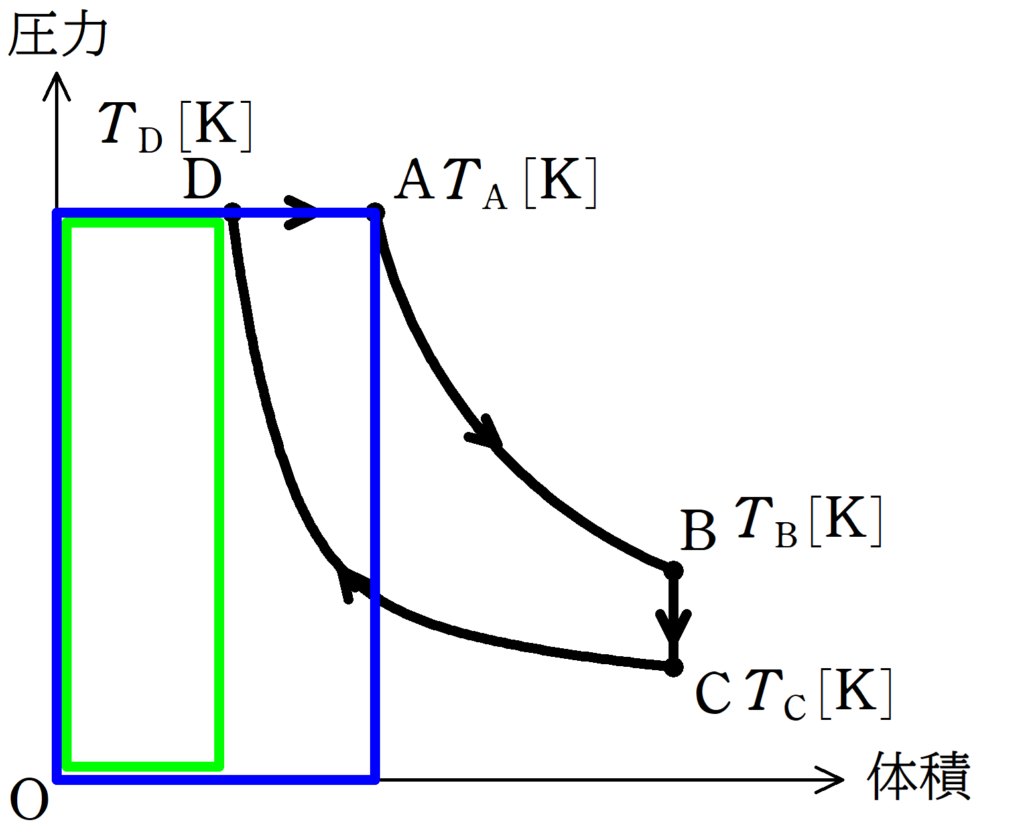

緑の面積より,青の面積の方が大きいから,$T_{\rm D}<T_{\rm A}$
(2)
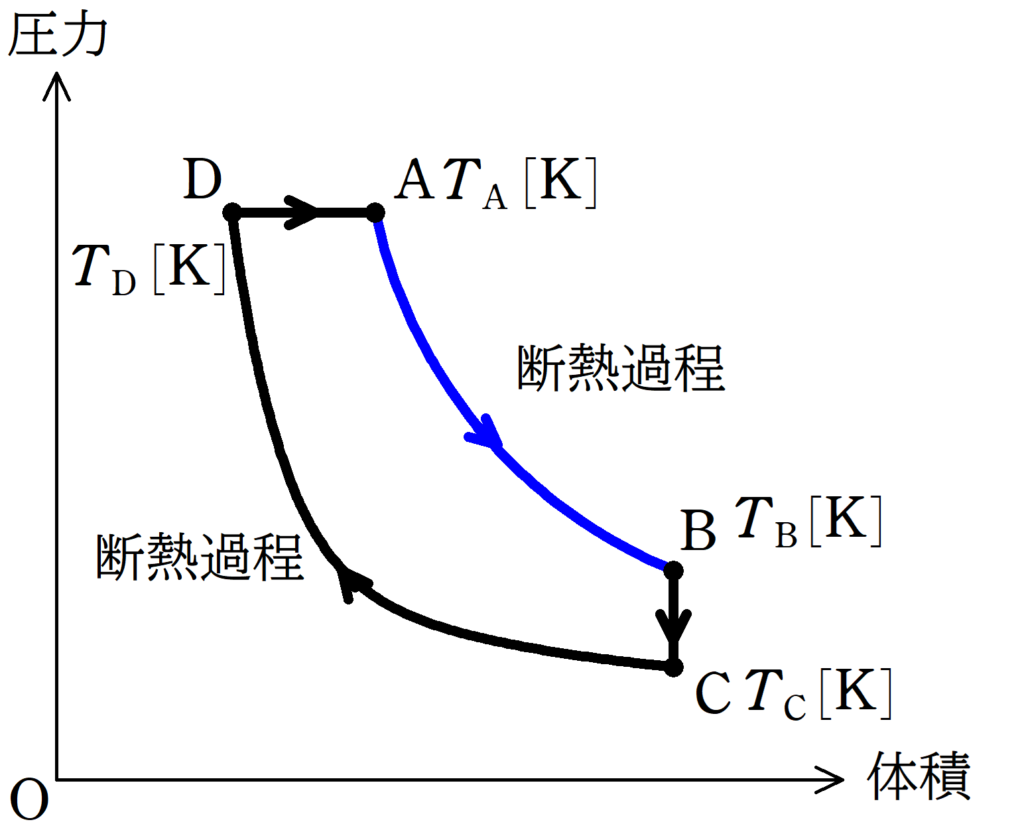

断熱過程や等温過程の気体がした仕事は$pV$グラフの面積で計算するのが大変だね.
そこで,熱力学第一法則を利用して,気体がした仕事$W_{\rm AB}$を求めます.
過程AからBの熱力学第一法則より
$Q_{\rm AB}=\Delta U_{\rm AB}+W_{\rm AB}$
断熱過程であるから,$Q_{\rm AB}=0$より
$W_{\rm AB}=-\Delta U_{\rm AB}$ $\dots (\ast)$
また,単原子分子理想気体の内部エネルギーの式より,物質量が$1\rm mol$であることも考慮して
$\Delta U_{\rm AB}=\dfrac{3}{2}R(T_{\rm B}-T_{\rm A})$ $\dots (2\ast)$
$(2\ast)$を$(\ast)$に代入して
$W_{\rm AB}=-\dfrac{3}{2}R(T_{\rm B}-T_{\rm A})=\dfrac{3}{2}R(T_{\rm A}-T_{\rm B})$

したがって,答えは
$W_{\rm AB}=\dfrac{3}{2}R(T_{\rm A}-T_{\rm B})[\rm J]$
です.
このように,$W_{\rm AB}$が正であることがわかるように変形しておくとよいでしょう.
(3)
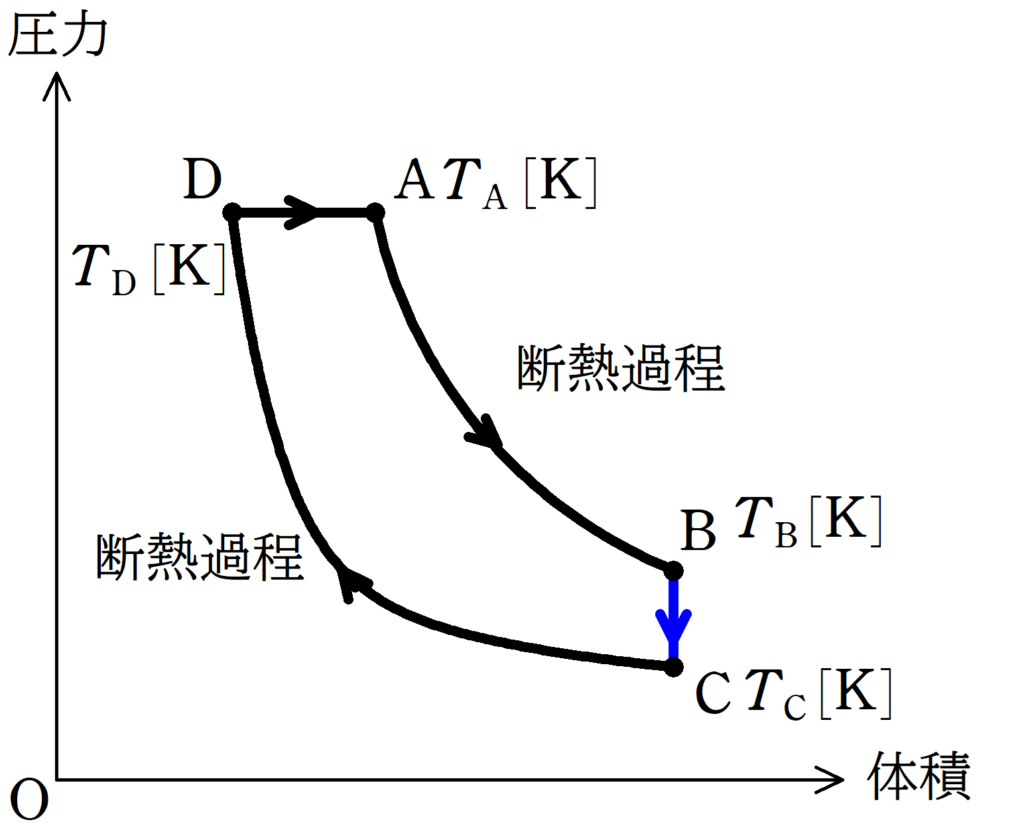

同様にして内部エネルギーの式と熱力学第一法則を使って,熱量$Q_{\rm BC}$を求めます.
★ 内部エネルギーの式より
$\Delta U_{\rm BC}=\dfrac{3}{2}R(T_{\rm C}-T_{\rm B})=-\dfrac{3}{2}R(T_{\rm B}-T_{\rm C})$ $\dots (3\ast)$
★ 熱力学第一法則
定積変化であるから,$W_{\rm BC}=0$であることを考慮して
$Q_{\rm BC}=\Delta U_{\rm BC}+W_{\rm BC}=-\dfrac{3}{2}R(T_{\rm B}-T_{\rm C})$
答えは$Q_{\rm BC}=-\dfrac{3}{2}R(T_{\rm B}-T_{\rm C})[\rm J]$
(4)
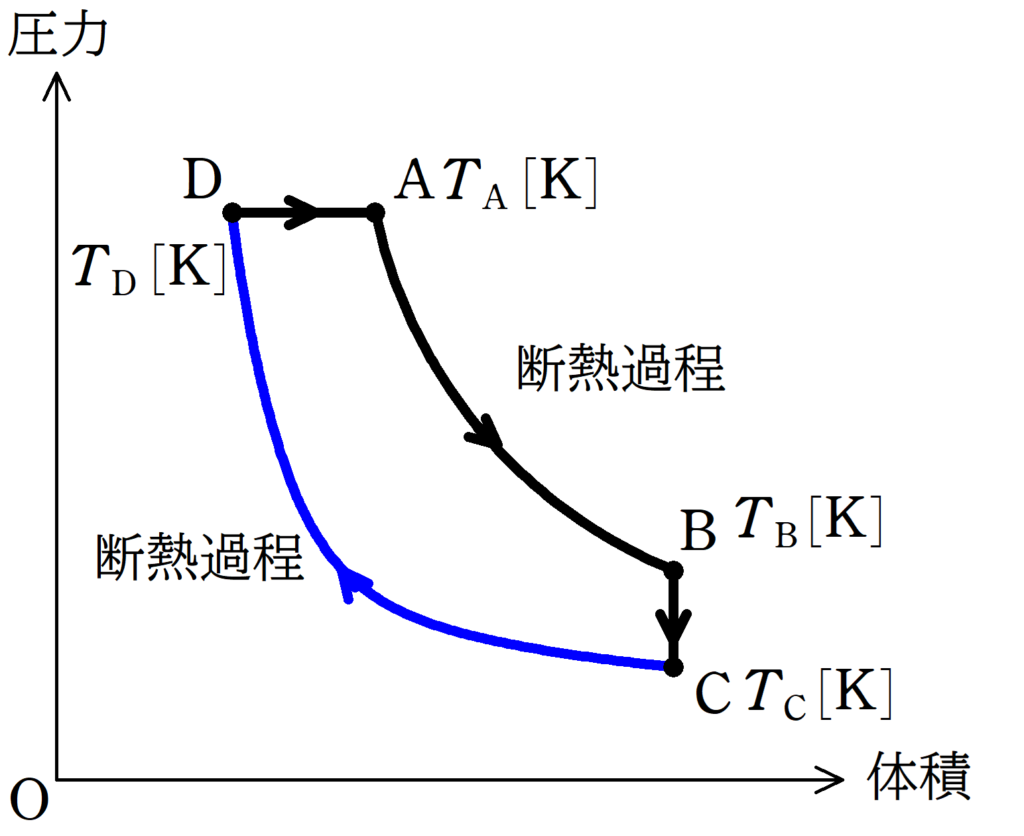
★ 内部エネルギーの式より
$\Delta U_{\rm CD}=\dfrac{3}{2}R(T_{\rm D}-T_{\rm C})$
★ 熱力学第一法則
断熱過程であるから,$Q_{\rm CD}=0$であることも考慮して
$0=\Delta U_{\rm CD}+W_{\rm CD}$
$\therefore W_{\rm CD}=-\Delta U_{\rm CD}=-\dfrac{3}{2}R(T_{\rm D}-T_{\rm C})$
答えは,$W_{\rm CD}=-\dfrac{3}{2}R(T_{\rm D}-T_{\rm C})[\rm J]$
(5)

DからAの気体がした仕事は,直線と$V$軸で囲まれた面積で計算できます.
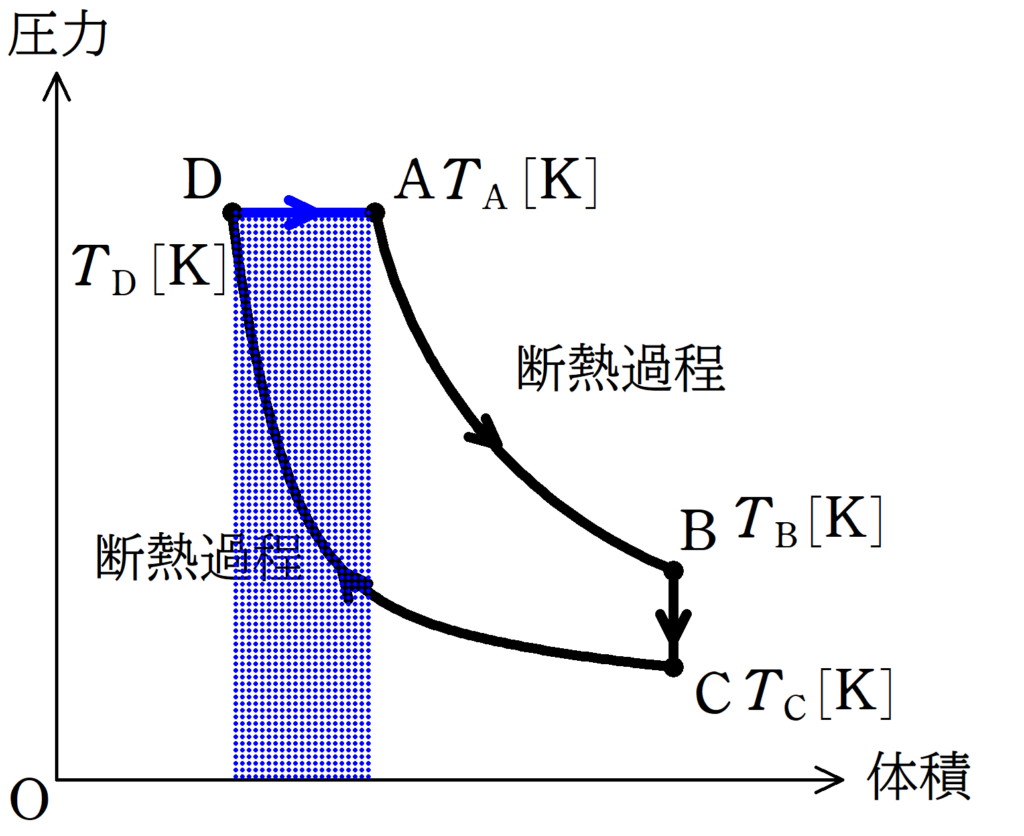

上図の青色部分の面積$S$は,D,Aの圧力を$p$,体積の変化を$\Delta V$とすると,
$S=p\Delta V$
だね.ただ,$p$や$\Delta V$は問題文に書かれていないから,状態方程式で変形すると
$S=p\Delta V=1\cdot R\Delta T=R(T_{\rm A}-T_{\rm D})$
となります.
したがって,$W_{\rm DA}=R(T_{\rm A}-T_{\rm D})[\rm J]$
★ 内部エネルギーの式より
$\Delta U_{\rm DA}=\dfrac{3}{2}R(T_{\rm A}-T_{\rm D})$
★ 熱力学第一法則より
$\eqalign{Q_{\rm DA}&=\Delta U_{\rm DA}+W_{\rm DA}\\&=\dfrac{3}{2}R(T_{\rm A}-T_{\rm D})+R(T_{\rm A}-T_{\rm D})\\&=\dfrac{5}{2}R(T_{\rm A}-T_{\rm D})}$
したがって,$Q_{\rm DA}=\dfrac{5}{2}R(T_{\rm A}-T_{\rm D})[\rm J]$

問題が多くて大変だったけど,熱力学第一法則や内部エネルギーの式の計算練習にはちょうどいいね.

コメント
[…] […]