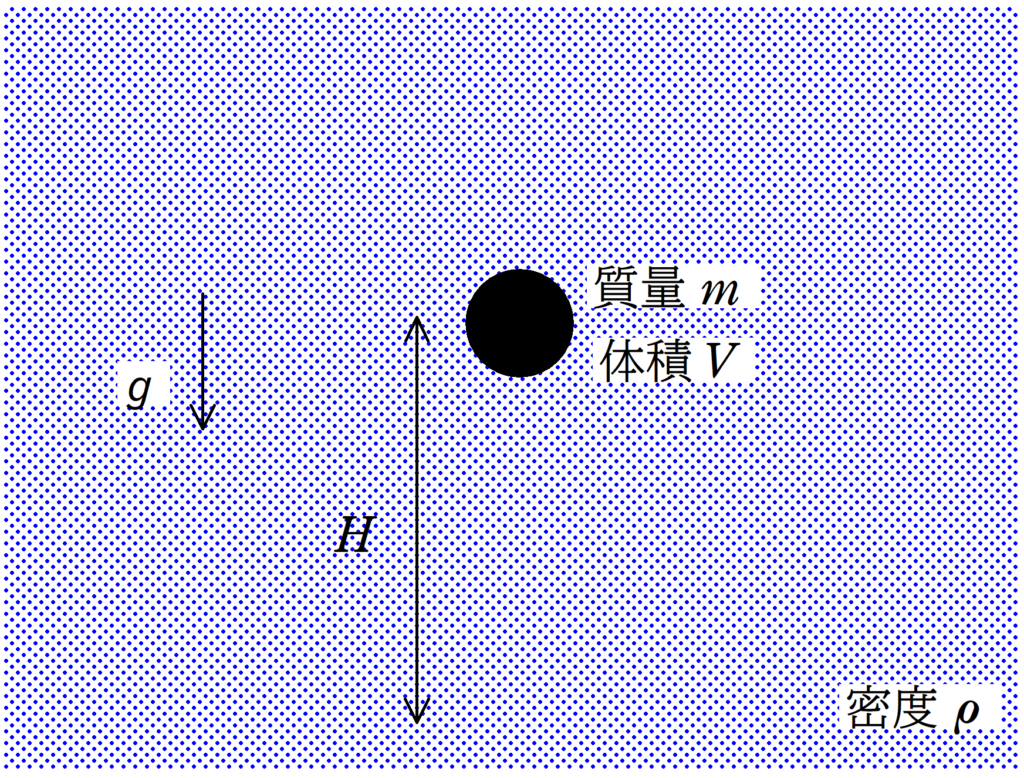
図のように,質量$m$,体積$V$の物体を密度$\rho$の液体中に静止させてある.
この物体を静かにはなしたところ,物体は鉛直下向きに運動を始めた.重力加速度の大きさを$g$として次の問いに答えよ.ただし,液体による抵抗は無視する.
(1) 物体が運動しているときの加速度の大きさ$a$を,$m$,$\rho$,$V$,$g$を用いて表せ.
(2) 運動を始めてから$H$だけ鉛直下向きに移動するまでの間にかかる時間$t_{1}$を求めよ.
(3) 運動を始めてから$H$だけ鉛直下向きに移動したときの速度$v_{1}$を求めよ.
(4) 速さに比例する抵抗がはたらく場合,十分時間が経つと,物体の速度は一定となる.この一定値$v_{2}$を求めよ.ただし液体による抵抗の正の比例定数を$k$とする.
<解答>
(1)

加速度を求めるので,運動方程式を立てましょう.
はたらく力は鉛直下向きに重力$mg$と,鉛直上向きに浮力$\rho Vg$です.
浮力については,アルキメデスの原理に従いましょう.
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.
★ 運動方程式
鉛直下向きに加速度$a$をとって,運動方程式を立てると
$ma=mg-\rho Vg$
$a=\left(1-\dfrac{\rho V}{m}\right)g$(答)
(2)

(1)より,等加速度運動をするので,等加速度運動の式を立てましょう.
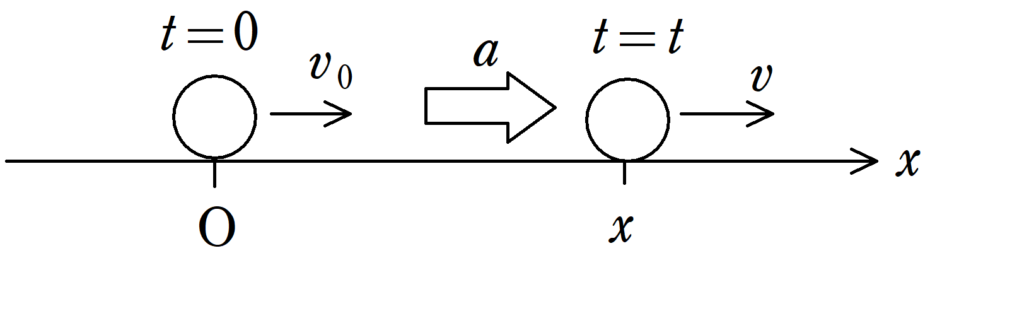
物体は加速度$a$で$x$軸上を運動している.$t=0$において,原点にある物体が,時刻$t$に座標$x$に移動した.初速度を$v_{0}$,時刻$t$における速度を$v$とするとき,次の関係式が成り立つ.
$v=v_{0}+at$ $\dots (\ast)$
$x=v_{0}t+\dfrac{1}{2}at^2$ $\dots (2\ast)$
$v^{2}-v_{0}^{2}=2ax$ $\dots (3\ast)$
★ 等加速度運動の式(2\ast)
$H=\dfrac{1}{2}at_{1}^{2}$
$t_{1}=\sqrt{\dfrac{2H}{a}}$
$a=\left(1-\dfrac{\rho V}{m}\right)g$より
$t_{1}=\sqrt{\dfrac{2H}{g-\dfrac{\rho Vg}{m}}}=\sqrt{\dfrac{2mH}{(m-\rho V)g}}$ (答)
(3)

同じく等加速度運動の式を立てましょう.
$(3\ast)$の式を立てます.
★ 等加速度運動の式$(3\ast)$
$v_{1}^{2}-0^{2}=2aH$
$v_{1}=\sqrt{2aH}$
$a=\left(1-\dfrac{\rho V}{m}\right)g$より
$v_{1}=\sqrt{2gH\left(1-\dfrac{\rho V}{m}\right)}$ (答)(向きは鉛直下向き)
(4)

速度が一定になると書いてあるので,加速度が$0$すなわち,力の和が0となります.
鉛直下向きに重力$mg$,鉛直上向きに浮力$\rho Vg$と抵抗力$kv_{2}$がはたらきます.
★ 力のつり合い
$\rho Vg+kv_{2}=mg$
$\therefore v_{2}=\dfrac{m-\rho V}{k}g$ (答)



コメント