
浮力の大きさは次のアルキメデスの原理を使えば,簡単に計算できるね.
でも,なんでこういう計算になるんだろう??
物体にはたらく浮力の大きさは,物体がおしのけた液体(または気体)の重さと等しい.
おしのけた液体(または気体)の密度を$\rho$,押しのけた分の物体の体積を$V$,重力加速度の大きさを$g$とすると,浮力の大きさ$F$は
$F=\rho Vg$
※ $\rho$は物体の密度ではなく,おしのけた液体(または気体)の密度である.

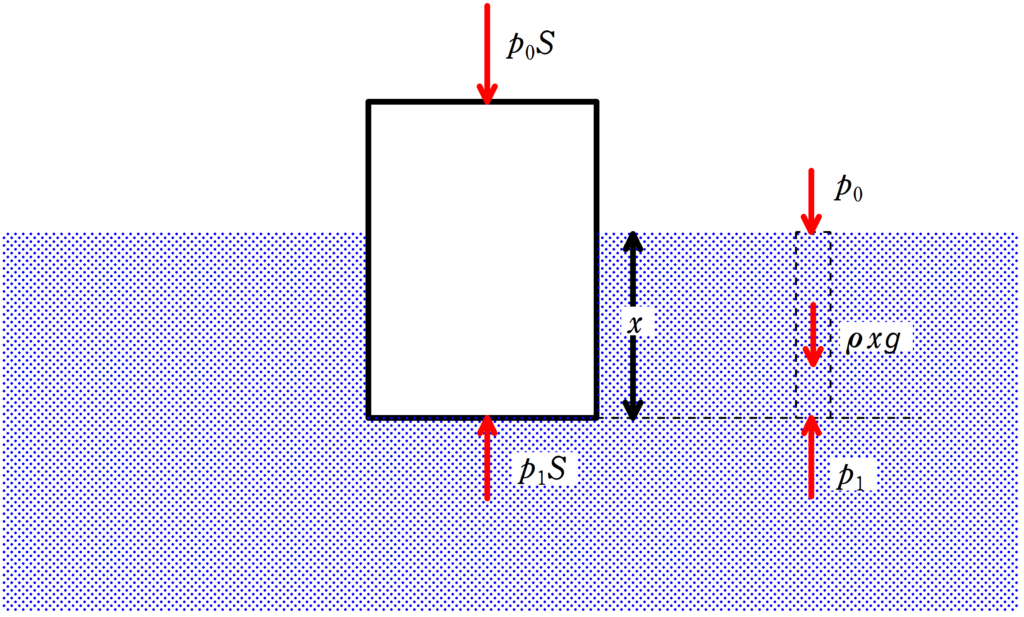
次図のように,密度が$\rho$の液体に断面積$S$の円柱の長さ$x$の部分が液体に入っている状態を考えましょう.
大気は円柱の上面を押し,液体が円柱の下面を押します.
この力の差を浮力と呼びます.
もし,円柱が液体にすべて浸っていれば,上からも下からも液体を押し,この力の差を浮力と呼びます.

では,浮力の大きさを計算しましょう.
(ただし,大気圧は一定としましょう.すなわち,円柱が気体をおしのけた分の浮力は無視します.)
大気圧を$p_{0}$とすると,圧力は単位面積当たりにはたらく力なので,大気が円柱上面を押す力は$p_{0}S$です.
また,下の記事でも書かれているように,「深さが同じ場所では同じ圧力」がかかります.
そこで,深さ$x$における液体の圧力を計算します.
単位面積の底面をもち,高さ$x$の円柱に切り取った液体にはたらく力について考えます.(上図の点線部分)
大気が押す力は,$p_{0}\cdot 1$,液体の重力は$\rho \cdot 1\cdot x g$($g$は重力加速度の大きさ)とし,深さ$x$部分の液体から押される力を$p_{1}\cdot 1$としましょう.
★ つり合いの式
$p_{1}=p_{0}+\rho xg$ $\dots (\ast)$

下側からおされる力が$p_{1}S$,上側から押される力が$p_{0}S$だからこの力の差$F$は次のようになるね.
$F=p_{1}S-p_{0}S=\rho Sxg$ $(\therefore (\ast))$

この力$F$は確かに,アルキメデスの原理と同じ,物体が液体を押しのけた分の重さになっているね.
でも,円柱じゃない場合もこれは成り立つのかな.
もっと複雑な形状のときはどう考えるんだろう.
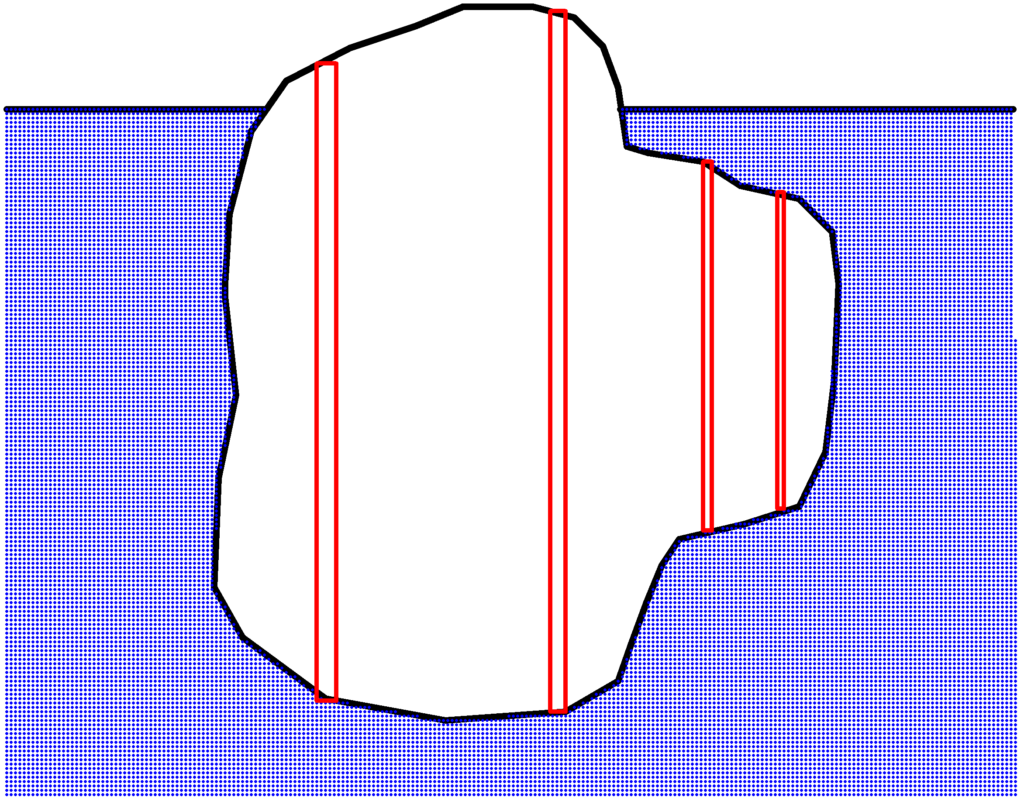

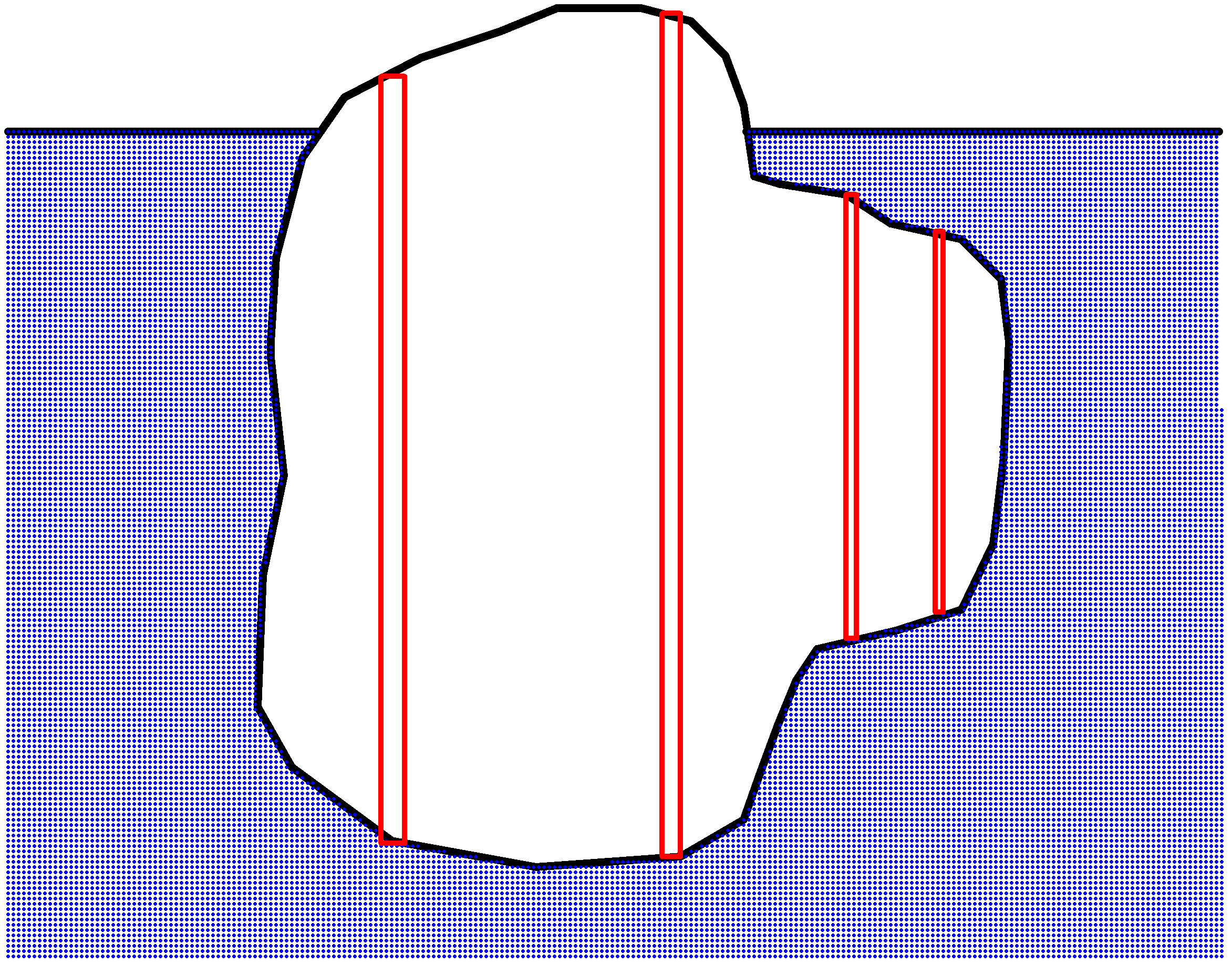
そのような場合は,断面積が非常に小さい円柱に分割すれば,はじめの議論が通じます.
各円柱は液体をおしのけた分の重さの分だけ鉛直上向きに浮力がはたらくので,結局,複雑な形状の場合についても,液体をおしのけた重さの分だけ鉛直上向きに力がはたらきます.
※ 断面が水平面と平行にならない場合も結局アルキメデスの原理の式は成り立ちます.

なるほど!


コメント