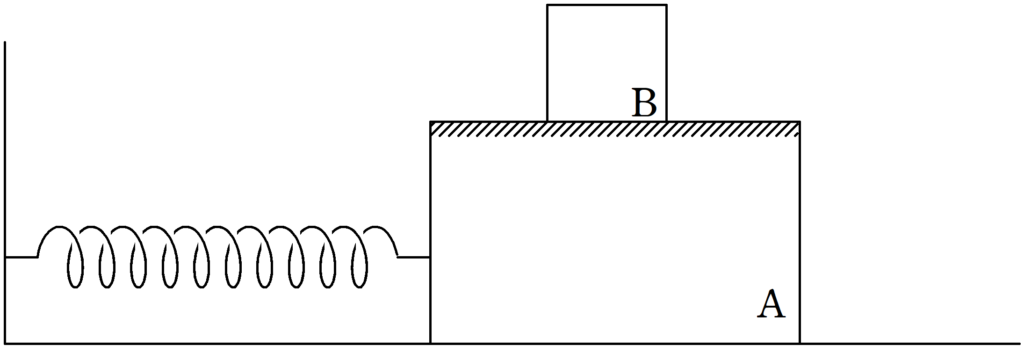
上図のように,水平な床の上に,質量$M$の台Aがあり,Aは,ばね定数$k$の軽いばねにつながれている.
ばねの他端は壁に固定されていて,はじめは自然長の状態でAとともに静止している.
Aの上に,質量$m$のBが置かれている.
Aと水平な床の間には,摩擦力がはたらかないが,AとBの間には摩擦力がはたらき,静止摩擦係数を$\mu$とする.
いま,Aを自然長の状態から距離$l$だけ右へ移動させ,その後手を放すとAとBは初速度0で単振動をはじめた.
このとき,BがAの上をすべらないで単振動するための$l$の条件を求めよ.
<解答>

単振動の問題なので,まずは運動方程式を立てて運動を把握しましょう.
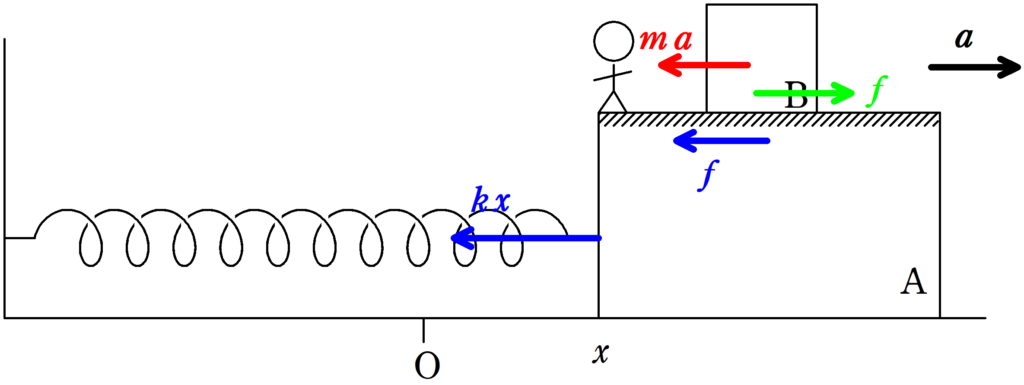

自然長を原点として,上図の右向きを正とします.
Aの左端が座標$x$のときの運動方程式を立てます.
AとBの加速度を$a$とします.
すると,Aの上にいる観測者からみたら,Bにはたらく力は慣性力$ma$と静止摩擦力$f$がはたらきます.
また,Aには,弾性力$kx$と,Bの間の摩擦力$f$がはたらきます.
★ Aの運動方程式
$Ma=-kx-f$ $\dots (\ast)$
★ AからみたBのつり合い(または,Bの運動方程式)
$ma=f$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より$f$を消去して,$a$を求める.
$(M+m)a=-kx$ $\dots (\heartsuit)$
$\therefore$ $a=-\dfrac{k}{M+m}x$
さらに,この結果を$(2\ast)$に代入して
$f=m\cdot (-\dfrac{k}{M+m}x)$ $\dots (\clubsuit)$

$(\clubsuit)$の結果から,静止摩擦力の大きさ$|f|$は
$|f|=\dfrac{mk}{M+m}|x|$
となるんだね.
だから,静止摩擦力の大きさは原点からの距離で決まるんだね.

一方,$(\heartsuit)$の運動方程式から,振動の中心は原点なので,振幅は,はじめに引き伸ばした距離$l$になるね.
ということは,静止摩擦力の最大値$f_{\rm max}$は
$f_{\rm max}=\dfrac{mk}{M+m}l$
となるんだ.
この摩擦力が最大静止摩擦力$\mu mg$を超えなければいいんだね.
★ すべらない条件
$\dfrac{mk}{M+m}l\leqq \mu mg$
$\therefore$ $l\leqq \dfrac{\mu (M+m)g}{k}$

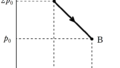
コメント